Area of the Polygon is the area enclosed by the boundary of the polygon. A polygon is a closed, two-dimensional shape with straight sides. Each side of a polygon is a line segment, and the points where the sides meet are called vertices.
 Area of Polygons
Area of PolygonsA polygon is a figure formed by joining 'n' straight lines such that it forms a closed figure. It has n-sides and there are different types of polygon, such as triangle, square, pentagon, etc. The area of the polygon is found by various methods and different types of polygons have different formulas to calculate its area. For example, suppose we have to find the area of a square (4-sided polygon) then its area is found by the formula, (side)2. Similarly, the area of other polygons is found.
Let's learn more about Area of Polygons with formula, derivation and examples in detail below.
Area of Polygon Definition
We define the area of the polygon as the space by a polygon. Suppose we have a n-sided polygon then the area enclosed by all its n-sides is called the area of that polygon. the area of the polygon is measured in the unit square, i.e. it is measured in m2, cm2, etc.
We can also say that area of the polygon is the space occupied by the polygon in a 2-Dimensional plane. Finding the area of the polygon is very important and we can find the area of the polygon by dividing the polygon into two types. before learning more about the area of a polygon let's first learn about the type of polygon.
Types of Polygon
The two types of polygons are,
- Regular Polygon
- Irregular Polygon
Regular Polygon
A polygon with all n-sides equal is called a Regular Polygon. Examples of regular polygons are Equilateral Triangles, Squares, Regular Pentagons, etc. The area of these regular polygons is easily calculated by using various formulas.
Irregular Polygon
A polygon in which all n-sides are not equal is called an Irregular Polygon. Examples of irregular polygons are Scalene Triangles, Rectangles, etc. Area of an irregular polygon is calculated by using various formulas by dividing these polygons into various known regular polygons and then finding their individual area and then adding them to get the required area of the polygon.
We will learn more about the area of polygon below in this article.
As we already know the area of polygon is found by using various formulas for both Regular polygons and Irregular polygons. Here are the formulas for some common polygons that we encountered in our daily lives.
Area of Regular Polygons
A regular polygon is a polygon that has equal sides and equal angles. Thus, the technique to calculate the value of the area of regular polygons is based on the formulas associated with each polygon. Let us have a look at the formulas of some commonly used regular polygons. The table added below shows Regular Polygon and the formulas for calculating their areas.
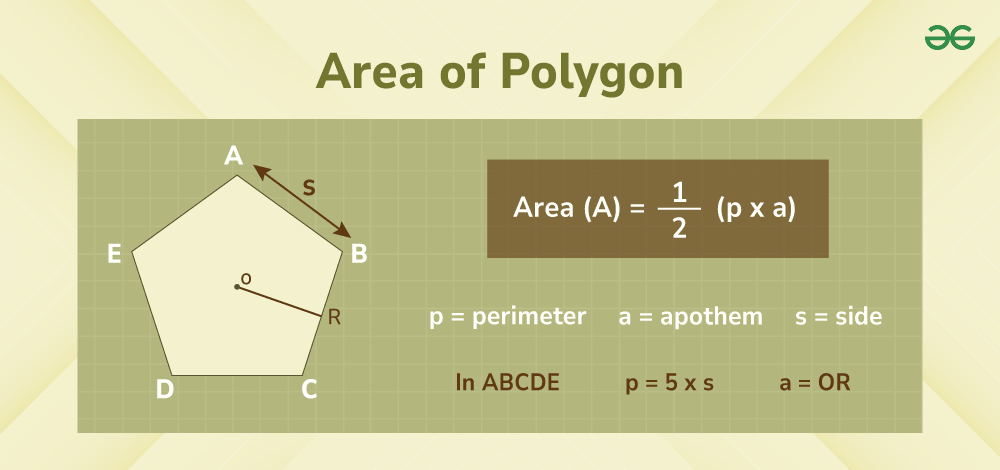
Now we see that the formula for area is different for different types of polygons. Suppose we have to give a common formula to find the area of the regular polygon. Then the formula for the same is,
A polygon having equal sides and equal angles is a regular polygon.
Area of Regular Polygon = (½) × Perimeter × Apothem
Area of Regular Polygon = (½) × (Number of Sides) × (Length of One Side) × (Apothem)
The use of this formula is explained in the example added below,
Example: Find the area of the regular polygon if the perimeter of the polygon is 20 cm and Apothem is 5 cm.
Solution:
Given,
- Perimeter of Polygon = 20 cm
- Length of Apothem = 5 cm
Area of Regular Polygon(A) = (½) × Perimeter × Apothem
A = (½) × 20 cm × 5 cm
A = 50 cm2
Thus, the area of the regular polygon is 50 cm2
Area of Irregular Polygon
An irregular polygon is a polygon in which all the sides are unequal. To find the area of an irregular polygon we first divide the Irregular Polygon into smaller polygons such as triangles and quadrilateral and then the area of smaller polygons are found and then sum the of all the polygons is found which gives the area of the irregular polygon.
The same can be explained using the example added below:

Area of Quadrilateral(ABCD) = (Area of Triangle ABC) + (Area of Triangle ACD)
In the above figure, the diagonal AC will act as a common base of the two triangles ABC and ADC with heights h1 and h2 respectively.
Area of Quadrilateral (ABCD) = Area of Triangle (ABC) + Area of Triangle (ACD)
Area of Quadrilateral (ABCD) = (1/2) × AC × h1 + (1/2) × AC × h2
Area of Quadrilateral (ABCD) = (1/2) × AC × (h1 + h2)
Thus, the area of the regular polygon is easily found.
Area of Polygons with Coordinates
If the coordinates of any polygon are given then its area is calculated using the steps discussed below.
Step 1: First find the distance of all the sides of the polygon, using the distance formula as,
D = √{(x2 - x1)2 + (y2 - y1)2}
Step 2: Finding all the sides of the polygon we first check whether the polygon is a regular polygon or not.
Step 3: Now, if the polygon is a regular polygon then use the formula,
Area of Regular Polygon = (Number of Sides × Length of One Side × Apothem)/2
Step 4: If the polygon is an irregular polygon then its area is calculated by dividing the polygon into smaller polygons then the area of the smaller polygon is found using the known formula. And then the sum is found which gives the area of the irregular polygon.
Example: Find the area of the polygon with coordinates A(1, 1), B(4, 1), C(1, 3), and D(4, 3)
Solution:
AB = √{(3)2 + (0)2} = 3
BC = √{(3)2 + (2)2} = √13
CD = √{(3)2 + (0)2} = 3
DA = √{(3)2 + (2)2} = √13
Here we see that AB = BC and CD = DA. Hence, ABCD is a rectangle
Therefore Area of Rectangle ABCD is 3√13
Difference Between Perimeter and Area of Polygons
Polygon is a closed figure formed by joining n-sides. Then its area is the space occupied by the boundary of the polygon. The difference between the perimeter and the area of the polygon is discussed in the table added below:
Perimeter of Polygon | Area of Polygon |
|---|
| Perimeter of a polygon is the sum of all the sides of the polygon. It is the length of all the boundaries of the polygon. | Area of the polygon is the space occupied by the boundary of the polygon or the total area enclosed by the polygon. |
| It is measured in units of length, i.e. it is measured in m, cm, etc. | It is measured in units of area, i.e. it is measured in m2, cm2,, etc. |
The formula to calculate the perimeter of an n-sided polygon is, Perimeter of Polygon = Length of First Side + Length of Second Side + ..... + Length of N side | The formula to calculate the area of the polygon is, Area of Polygon = (½) × Perimeter × Apothem |
Read More
Area of Polygon Examples
Example 1: Find the area of the given polygon.

Solution:
We are given the above figure which is a Hexagon and we are supposed to find out the area of the above figure MNOPQR.
Area of the figure MNOPQR = Area of triangle MNO + Area of triangle PQR + Area of rectangle MOPR
Area of the figure MNOPQR = (1/2) × MO × NK +(1/2) × PR × QL + PO × MO
Area of the figure MNOPQR = (1/2) × 20 × 5 + (1/2) x 20 × 5 + 13 × 20
Area of the figure MNOPQR = 10 × 5 + 10 × 5 + 260
Area of the figure MNOPQR = 50 cm2+ 50 cm2 + 260 cm2
Area of the figure MNOPQR = 360 cm2
Hence, the area of the given Hexagon MNOPQR is 360 cm2.
Example 2: Find the area of the given polygon.

Solution:
We are given the above figure which is a Hexagon and we are supposed to find out the area of the above figure ABCDEF.
Area of the figure ABCDEF = Area of Trapezium DEFC + Area of Square ABCF
Area of the figure ABCDEF = (1/2) × (ED+FC) × EK + (AF)2
Area of the figure ABCDEF = (1/2) × (7 + 18) × 8 + (18)2
Area of the figure ABCDEF = 4 × 25 + 18 × 18
Area of the figure ABCDEF = 100 cm2 + 324 cm2
Area of the figure ABCDEF = 424 cm2
Hence, the area of the given Hexagon ABCDEF is 424 cm2
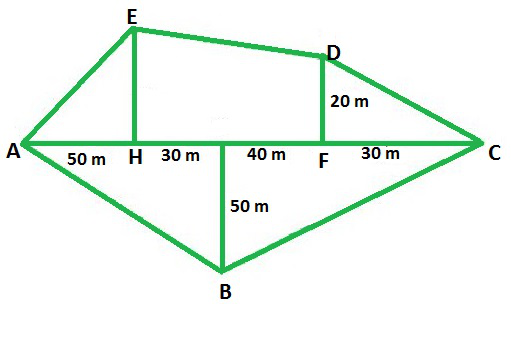
Example 3: Find the area of the given polygon.
Solution:
We are given the above figure which is a Pentagon and we are supposed to find out the area of the above figure ABCDE.
Area of the figure ABCDE = Area of triangle AHE + Area of Trapezium DEHF + Area of triangle DFC + Area of Triangle ABC
Area of the figure ABCDE = (1/2) × AH × HE + (1/2) × (EH+DF) × HF + (1/2)× FC × DF + (1/2) × AC × GB
Area of the figure ABCDE = (1/2) × 50 × 30 + (1/2) × (30+20) × 70 + (1/2) × 30 × 20 + (1/2) × 150 × 50
Area of the figure ABCDE = 25 × 30 + 50 × 35 + 15 × 20 + 150 × 25
Area of the figure ABCDE = 750 m2 + 1750 m2+ 300 m2+ 3750 m2
Area of the figure ABCDE = 6550 m2
Hence, the area of the given Pentagon ABCDE is 6550 m2.
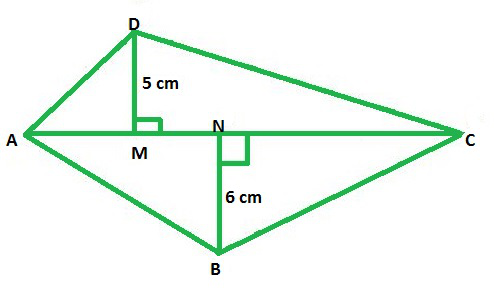
Example 4: Find the area of the given polygon, where the length of the diagonal AC is 18 cm.
Solution:
We are given the above figure which is a quadrilateral, and we are supposed to find out the area of the above figure ABCD.
Area of the quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC
Area of the quadrilateral ABCD = (1/2) × AC × DM + (1/2) × AC × BN
Area of the quadrilateral ABCD = (1/2) × AC × (BN+DM)
Area of the quadrilateral ABCD = (1/2) × 18 × (6+5)
Area of the quadrilateral ABCD = 9 × 11 cm2
Area of the quadrilateral ABCD = 99 cm2
Hence, the area of the given quadrilateral is 99 cm2.
Example 5: Find the area of the given polygon.

Solution:
We are given the above figure which is a Pentagon and we are supposed to find out the area of the above figure ABCDE.
Area of the figure ABCDE = Area of triangle AGB + Area of Rectangle BCHG + Area of triangle AFE + Area of Trapezium DEFH
Area of the figure ABCDE = (1/2) × AG × BG + BG × GH + (1/2) × AF × FE + (1/2) × (DH+EF) × FH
Area of the figure ABCDE = (1/2) × 8 × 4 + 4 × 3 + (1/2) × 5 × 5 + (1/2) × (3+5) × 6
Area of the figure ABCDE = 4 × 4 + 4 × 3 + 2.5 × 5 + 3 × 8 cm2
Area of the figure ABCDE = 16 + 12 + 12.5 + 24 cm2
Area of the figure ABCDE = 64.5 cm2
Hence, the area of the given Pentagon ABCDE is 64.5 cm2.
Example 6: Find the area of the given polygon.

Solution:
We are given the above figure which is a Pentagon, and we are supposed to find out the area of the above figure ABCDE.
Area of the figure ABCDE = Area of triangle ADE + Area of triangle CHD + Area of Trapezium BCHF + Area of triangle ABF
Area of the figure ABCDE = (1/2) *AD*GE + (1/2) *HD*CH + (1/2) *(CH+BF)*FH + (1/2) *AF*BF
Area of the figure ABCDE = (1/2) × 7 × 4 + (1/2) × 1 × 4 + (1/2) × (4+3) × 4 + (1/2) × 2 × 3 cm2
Area of the figure ABCDE = 2 × 7 + 2 + 7 × 2 + 1 × 3 cm2
Area of the figure ABCDE = 14 + 2 + 14 + 3 cm2
Area of the figure ABCDE = 33 cm2
Hence, the area of the given Pentagon ABCDE is 33 cm2.
Practice Questions on Area of Polygons
Q1: Find the Area of an Equilateral Triangle of side 6cm.
Q2: Find the Area of a rectangular park whose length is 10 m and breadth is 30 m.
Q3: What is the Area of Square whose diagonal is 6 cm.
Q4: What is the Area of a Rhombus whose diagonals measures 12 cm and 16 cm?
Q5: What is the Area of a Trapezium whose Parallel sides measures 6 and 12 cm and altitude is 8 cm?
Q6: Find the area of a regular pentagon with a side length of 5 cm.
Q7: A triangular garden has a base of 12 m and a height of 10 m. What is its area?
Q8: Calculate the area of a circle inscribed within a square whose side length is 4 m.
Q9: What is the area of a parallelogram with the base of 8 cm and a height of 5 cm?
Q10: A hexagonal plot of land has a side length of 10 m. Calculate its area.
Conclusion
The area of polygons is a fundamental concept in geometry that allows us to quantify the space enclosed by the various polygonal shapes such as the triangles, rectangles, pentagons and more. By utilizing the different formulas and methods tailored to specific types of polygons we can accurately calculate their areas. Understanding how to find the area is not only crucial for the academic purposes but also for practical applications in fields such as the architecture, engineering and land surveying. Mastery of these concepts enables better spatial reasoning and problem-solving skills in real-world scenarios.
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice