In many real-world situations, we often deal with a set of objects and the relationships between them. For example, cities connected by roads, people linked through friendships, or computers connected in a network. To study such relationships mathematically, we utilize graph theory.
Given below are some applications of graph theory in real life:
Graph Theory is a branch of mathematics that deals with graphs—structures made up of vertices (points) and edges (lines). These graphs help us model and solve problems in computer science, engineering, biology, logistics, and many other fields.
Definition of Graph
A graph is a mathematical structure used to represent a set of objects and the connections between them:
- The objects are called vertices ( or nodes),
- The connections between them are called edges (or links).
- Nodes: A finite non-empty set of points.
- Edges: A set of pairs of vertices that represent the connections between them.
 A Simple Graph
A Simple GraphFormally: A graph G is defined as: G - (V, E)
Where:
- V = a set of vertices (or nodes), representing objects.
- E = a set of edges (or links), representing connections between pairs of vertices.
Basic Concepts
Below are the basic terminologies used in graph theory.
Vertex (Node): A fundamental element of a graph, representing an object, entity, or point.
Edge (Link): A connection between two vertices, showing a relationship or pathway.
Adjacent Vertices: Two vertices that are directly connected by an edge.
Degree of a Vertex: The number of edges incident on a vertex.
- In a directed graph, we distinguish between in-degree (incoming edges) and out-degree (outgoing edges).
Path: A sequence of vertices connected by edges, with no vertex repeated.
Cycle: A path that begins and ends at the same vertex, forming a closed loop.
Connected Graph: A graph in which there exists a path between every pair of vertices.
Subgraph: A smaller graph formed using a subset of the vertices and edges of a larger graph.
Loop: An edge that connects a vertex back to itself.
Parallel Edges: Two or more edges that connect the same pair of vertices.

Explanation of the image above:
- Vertex (Node): The circles labeled in the graph.
Example: 1, 2, 3, 4, 5, 6 are vertices.
- Edge (Link): The lines connecting two vertices.
Example: The line between vertex 3 and 5 is an edge.
- Adjacent Vertices: Vertices that are directly connected by an edge.
Example: 3 and 5 are adjacent because they share an edge.
- Degree of a Vertex: The number of edges incident on a vertex.
Example: Vertex 3 has degree 3 (connected to 1, 4, and 5).
- Path: A sequence of vertices connected by edges.
Example: One path is 5 → 3 → 1 → 2 → 6.
- Cycle: A path that starts and ends at the same vertex, without repeating edges.
Example: 1 → 3 → 4 → 2 → 1 forms a cycle.
- Connected Graph: A graph where there is a path between every pair of vertices.
Example: From vertex 5, we can reach vertex 6 via 5 → 3 → 2 → 6, so this graph is connected.
Types of Graphs
Graphs are of two types based on the type of edge, these are:
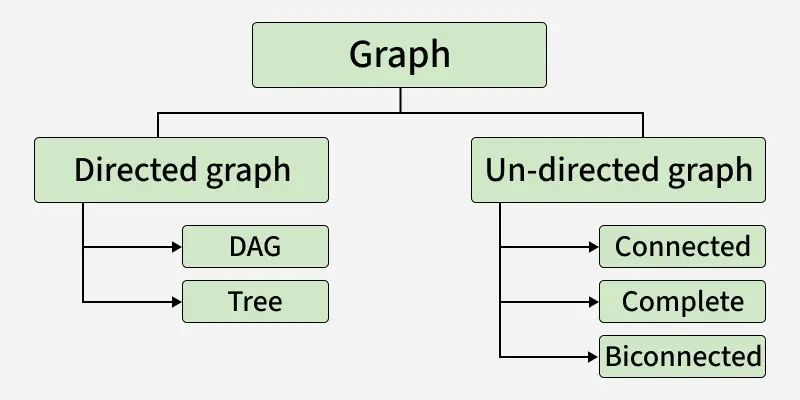 Graph Classification
Graph ClassificationLet's discuss the types in detail.
Directed Graph
A graph in which the direction of the edge is defined for a particular node is a directed graph.
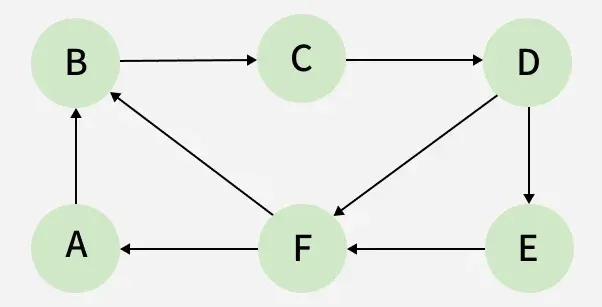
Directed Acyclic: It is a directed graph with no cycle. For a vertex ‘v’ in DAG, there is no directed edge starting and ending with vertex ‘v’. The arrows go in one direction only (Directed), and you can’t go in a circle or loop (Acyclic).
Tree: A tree is just a restricted form of graph. That is, it is a DAG with a restriction that a child can have only one parent.
Undirected Graph
A graph in which the direction of the edge is not defined. So if an edge exists between node ‘u’ and ‘v’, then there is a path from node ‘u’ to ‘v’ and vice versa.
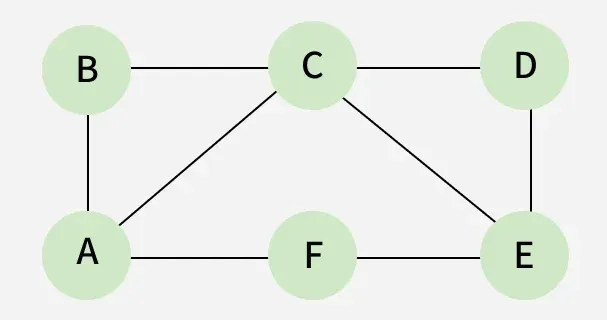
Connected graph: A graph is connected when there is a path between every pair of vertices. In a connected graph, there is no unreachable node.
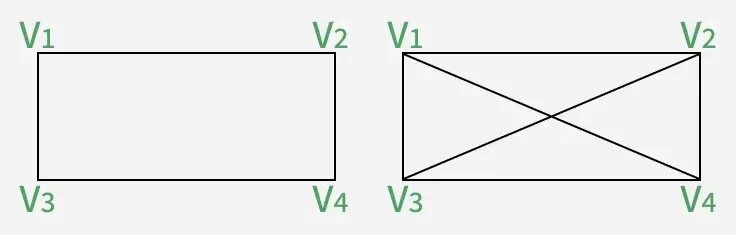
Complete graph: A graph in which each pair of graph vertices is connected by an edge. In other words, every node ‘u’ is adjacent to every other node ‘v’ in graph ‘G’. A complete graph would have n(n-1)/2 edges.
Biconnected graph: A connected graph that cannot be broken down into any further pieces by the deletion of any vertex. It is a graph with no articulation point.
Some Important Graphs
1. Regular Graph: A graph in which every vertex x has the same/equal degree. A K-regular graph means every vertex has k edges. Every complete graph Kn will have (n-1)-regular graph, which means the degree is n-1.
 Regular Graphs
Regular Graphs2. Bipartite Graph: It is a graph G in which the vertex set can be partitioned into two subsets U and V such that each edge of G has one end in U and another end point in V.
 Bipartite Graph
Bipartite Graph3. Complete Bipartite graph: It is a simple graph with a vertex set partitioned into two subsets, u and w.
U = {v1, v2 , v3, ..., vm} and W = {w1, w2, w3, ..., wn}
The elements in these sets are the vertices.
- There is an edge from each vi to each wj.
- There is no self-loop.
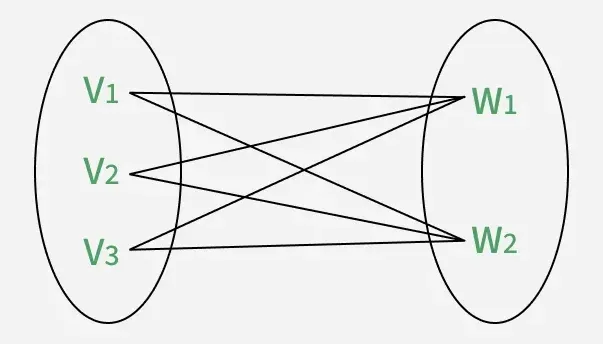 Complete Bipartite graph
Complete Bipartite graph4. Cycle graph: It is a connected graph where each vertex has degree 2, forming a single closed loop without any branches or endpoints. This graph contains at least 3 vertices. Suppose a graph has the following vertices:
v1, v2, v3, ..., vn
This graph will be a cycle graph if it has edges as follows:
(v1,v2), (v2,v3), (v3,v4), ..., (vn-1,vn), (vn,v1).
 Cycle Graphs
Cycle GraphsApplications of Graph Theory in CS
The major applications of Graph Theory in Computer Science are:
- Computer Networks – Graphs help in finding the shortest and most efficient path for data transfer between computers.
- Social Networks – People are nodes, and connections are edges. Graphs are used for friend suggestions and finding influencers.
- Operating Systems – Resource Allocation Graphs detect deadlocks by checking for cycles.
- Compiler Design – Control Flow Graphs show program execution flow, and graph coloring is used for register allocation.
- Search Engines (Web Graphs) – The internet is a huge directed graph of web pages. PageRank uses graph theory to rank search results.
Solved Question on Basic Graph Theory
Question 1: For V = {1, 2, 3, 4}, find all unordered pairs and total edges in K4.
Solution:
Unordered pairs =
{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}
Total = 6 edges.
Formula check: (n(n − 1))/2 = (4 × 3)/2 = 6
Question 2: Graph with edges E = {{A, B}, {B, C}, {C, D}, {D, A}}. Find the order and size of the graph and determine the degree of each vertex.
Solution:
- This is a square cycle C4.
- Degrees: deg(A) = 2, deg(B), deg(C) = 2, deg(D) = 2
Unsolved Question on Basic Graph Theory
Question 1: Graph with vertices V = {1, 2, 3, 4, 5}. Find the number of edges in the complete graph K5.
Question 2: Graph with edges E = {{1, 2}, {2, 3}, {3, 4}, {4, 5}}. Find the order, size, and degree of each vertex.
Question 3: Find the number of edges and degree of each vertex in the complete bipartite graph K3,4.
Question 4: Find the number of spanning trees in K4.
Explore
Maths
4 min read
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice