Pathfinder Optimization Algorithm
Last Updated :
06 Oct, 2021
Nature is full of social behaviours for performing different tasks. Although the ultimate goal of all individuals and collective behaviours is survival, creatures cooperate and interact in groups, herds, schools, colonies, and flocks for several reasons: hunting, defending, navigating, and foraging. In order to mimic these characteristics of animals, swarm-intelligence based optimization algorithms are introduced.
For example – Ant Colony optimization, Cat Swarm Optimization, Particle Swarm optimization
Inspiration
A pathfinder simply is the individual which leads a swarm. This entity leads the swarm and this entity leads various acts. In addition, this entity takes the swarm to destinations including pastures, water and feeding areas. The group of animals frequently decide the movement between members via social order. Such animals may either have to decide with the leader or with no leader. Leadership however is temporary, with few people knowing the place, hunting area, route, etc.
Mathematical Model
The population basically follows the pathfinder for various activities. However, in order to do so, we need to specify the position of both the pathfinder and any arbitrary population member. The position of a member says Xi is defined as:

Where Xi is the position vector of ith follower at k iteration, r1 and r2 are random variables uniformly generated in the range of [0,1], α is the coefficient for interaction and β is the coefficient of attraction. The value of α, ß are set in such a way that there is the perfect balance between interaction (i.e. the magnitude of movement of any member together with its neighbour) and attraction (i.e. the random distance for keeping the herd roughly with the leader). The optimum values for α, ß should be around 1. ε is the vector of vibration and it is defined as follows:

where,  , u1 is random variable in range [-1,1]
, u1 is random variable in range [-1,1]
The position of pathfinder is defined as:
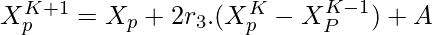
Xp is the position vector of the pathfinder, K is the current iteration, r3 if a random variable in the range of [0,1], A is the vector of fluctuation rate. A is defined as follows:

where u2 is a random variable in the range [-1,1], Kmax is the maximum iteration.
ε, A can provide random movement (walk) for all members. Therefore setting different values for them ensures exploration and exploitation. The term  in ε, A ensures exploration and exploitation phases of a metaheuristic technique. At first
in ε, A ensures exploration and exploitation phases of a metaheuristic technique. At first  is very small, thereby resulting in rapid change constituting to exploration. Then at later stages, its value becomes eventually small or even zero, constituting exploitation.
is very small, thereby resulting in rapid change constituting to exploration. Then at later stages, its value becomes eventually small or even zero, constituting exploitation.
Algorithm
- Define the parameters such as r1, r2, ε, A
- Initialize the population and calculate fitness for each member
- Set the best fitness value as the pathfinder
- while iteration condition is not met or till max iteration do
- Generate α, ß in range [0, 1]
- Using the pathfinder equation update the position of pathfinder
- If fitness of current pathfinder is better than old pathfinder Then
- Update fitness of the pathfinder
- For i=1 to population size
- Update position of followers using followers equation.
- Update fitness values of each member
- Find the best fitness
- If best fitness is better than old pathfinder Then
- Update fitness of the pathfinder
- For i=1 to population size
- If new fitness of the member is better than old fitness Then
- Update fitness of member
- Generate ε, A
- End
The best position and fitness is returned and can be used to solve optimization problems.
References: https://www.sciencedirect.com/science/article/pii/S1568494619301309
Similar Reads
Whale Optimization Algorithm (WOA)
The step-by-step procedure to obtain an optimum value (maximum or minimum) of an objective function is called an Optimization Algorithm. Meta-heuristic optimization algorithms are becoming more and more popular in engineering applications because they: rely on rather simple concepts and are easy to
3 min read
Brain storm optimization
Optimization is usually tasked to identify the best solution(s) for some specific problem. A problem with optimization in Rn or simply a problem with optimization is [Tex]f: R_n \rightarrow R_m [/Tex] , whereby Rn and Rm represent decision space and objective space respectively. The fitness value or
5 min read
Implementation of Whale Optimization Algorithm
Previous article Whale optimization algorithm (WOA) talked about the inspiration of whale optimization, its mathematical modeling and algorithm. In this article we will implement a whale optimization algorithm (WOA) for two fitness functions 1) Rastrigin function   2) Sphere function  The algorithm
6 min read
Introduction to Optimization with Genetic Algorithm
Optimization is the process of finding the best solution after evaluating all possible combinations. When dealing with complex problems, finding the optimal solution becomes crucial. One powerful tool in machine learning for solving such optimization problems is the genetic algorithm. Inspired by th
10 min read
AO* algorithm in Artificial intelligence (AI)
The AO* algorithm is an advanced search algorithm utilized in artificial intelligence, particularly in problem-solving and decision-making contexts. It is an extension of the A* algorithm, designed to handle more complex problems that require handling multiple paths and making decisions at each node
15+ min read
Optimization Algorithms in Machine Learning
Optimization algorithms are the backbone of machine learning models as they enable the modeling process to learn from a given data set. These algorithms are used in order to find the minimum or maximum of an objective function which in machine learning context stands for error or loss. In this artic
15+ min read
Second-Order Optimization Methods
Second-order optimization methods are a powerful class of algorithms that can help us achieve faster convergence to the optimal solution. In this article, we will explore second-order optimization methods like Newton's optimization method, Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, and the C
13 min read
Artificial Intelligence (AI) Algorithms
Artificial Intelligence (AI) is transforming industries and revolutionizing how we interact with technology. With a rising interest in Artificial Intelligence (AI) Algorithms, we’ve created a comprehensive tutorial that covers core AI techniques, aimed at both beginners and experts in the field. The
9 min read
Dragon fly Optimization
Due to its simplicity, easy operation, capacity to protect against local optima, and the problem of derivatives free, Metaheuristic was frequently employed throughout the previous three decades. Exploration and exploitation are two fundamental metaheuristic features. The first one shows how the algo
4 min read
Uni-variate Optimization - Data Science
Optimization is an important part of any data science project, with the help of optimization we try to find the best parameters for our machine learning model which will give the minimum loss value. There can be several ways of minimizing the loss function, However, generally, we use variations of t
6 min read