Ambiguity in Context free Grammar and Languages

Context-Free Grammars (CFGs) are essential in formal language theory and play a crucial role in programming language design, compiler construction, and automata theory. One key challenge in CFGs is ambiguity, which can lead to multiple derivations for the same string.

Understanding Derivation in Context-Free Grammars

Suppose we have a context free grammar G with production rules:

S \rightarrow aSb \ | \ bSa \ | \ SS \ | \ \varepsilon

1. Left most derivation (LMD) and Derivation Tree

A leftmost derivation (LMD) is a sequence where the leftmost non-terminal is replaced first at every step.

Example: Leftmost Derivation of "abab"

S \Rightarrow aSb \Rightarrow abSab \Rightarrow abab

In this derivation, the underlined symbols indicate replacements based on the production rules.

Derivation tree: It tells how string is derived using production rules from S and has been shown in Figure below. 

2. Right most derivation (RMD)

A rightmost derivation (RMD) follows the same principle as LMD but replaces the rightmost non-terminal first at each step. 

Example: Rightmost Derivation of "abab"

S \Rightarrow SS \Rightarrow SaSb \Rightarrow Sab \Rightarrow aSbab \Rightarrow abab

Again, the underlined symbols indicate the replaced non-terminals. The derivation tree for RMD is shown in Figure below.

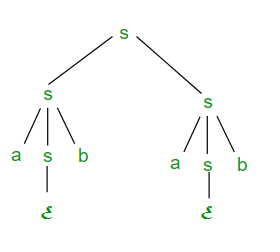
3. Comparing LMD and RMD

A derivation can be LMD, RMD, both, or neither.

Example of both LMD and RMD:

S \Rightarrow aSb \Rightarrow abSab \Rightarrow abab

Example of only RMD:

S \Rightarrow SS \Rightarrow SaSb \Rightarrow Sab \Rightarrow aSbab \Rightarrow abab

Ambiguity in Context-Free Grammars

A context-free grammar (CFG) is ambiguous if there exists more than one leftmost or rightmost derivation for the same string. As a result, ambiguous grammars lead to multiple derivation trees for a single string.

Example: For the grammar G, the string abab has multiple derivations:

1. Derivation 1 (RMD):

S \Rightarrow SS \Rightarrow SaSb \Rightarrow Sab \Rightarrow aSbab \Rightarrow abab

2. Derivation 2 (LMD & RMD):

S \Rightarrow aSb \Rightarrow abSab \Rightarrow abab

Since the grammar generates more than one derivation tree for abab, it is ambiguous.

Ambiguous Context-Free Languages (CFLs)

A context-free language (CFL) is called ambiguous if no unambiguous CFG can describe it. Such languages are also known as inherently ambiguous CFLs.

Key Observations:

• If a CFG is ambiguous, the corresponding language L(G) may or may not be ambiguous.
• It is not always possible to convert an ambiguous CFG into an unambiguous CFG.
• There exists no general algorithm to convert an ambiguous CFG into an unambiguous CFG.
• Every unambiguous CFL has at least one unambiguous CFG.
• Deterministic CFLs are always unambiguous.

Question: 

Consider the following context-free grammar:

G = \{ S \to SS, S \to ab, S \to ba, S \to \varepsilon \}

Which of the following statements about G are true?

I. G is ambiguous
II. G generates all strings with an equal number of "a" and "b"
III. G can be accepted by a deterministic PDA

Which option correctly identifies the true statements?

A) I only
B) I and III only
C) II and III only
D) I, II, and III

Solution:

Statement I is true: There are multiple leftmost derivations for the string abab, proving that G is ambiguous.
Statement II is false: G cannot generate strings like aabb, meaning it does not produce all strings with equal "a" and "b".
Statement III is true: G can be accepted by a deterministic PDA.

Correct Answer:

B) I and III only