What is Context-Free Grammar?
Last Updated :
23 Jul, 2025
A grammar consists of one or more variables that represent classes of strings (i.e., languages) . There are rules that say how the strings in each class are constructed. The construction can use :
- Symbols of the alphabet
- Strings that are already known to be in one of the classes
- Or both
Context-Free Grammar
A context-free grammar (CFG) is a formal system used to describe a class of languages known as context-free languages (CFLs). Purpose of context-free grammar is:
- To list all strings in a language using a set of rules (production rules).
- It extends the capabilities of regular expressions and finite automata.
A GFG (or just a grammar) G is a tuple G = (V, T, P, S) where
- V is the (finite) set of variables (or non terminals or syntactic categories). Each variable represents a language, i.e., a set of strings
- T is a finite set of terminals, i.e., the symbols that form the strings of the language being defined
- P is a set of production rules that represent the recursive definition of the language.
- S is the start symbol that represents the language being defined. Other variables represent auxiliary classes of strings that are used to define the language of the start symbol.
A grammar is said to be the Context-free grammar if every production is in the form of:
G -> (V∪T)* , where G ∊ V
- V (Variables/Non-terminals): These are symbols that can be replaced using production rules. They help in defining the structure of the grammar. Typically, non-terminals are represented by uppercase letters (e.g., S, A, B).
- T (Terminals): These are symbols that appear in the final strings of the language and cannot be replaced further. They are usually represented by lowercase letters (e.g., a, b, c) or specific symbols.
- The left-hand side can only be a Variable, it cannot be a terminal.
- But on the right-hand side here it can be a Variable or Terminal or both combination of Variable and Terminal.
The above equation states that every production which contains any combination of the 'V' variable or 'T' terminal is said to be a context-free grammar.
Core Concepts of CFGs
A CFG is defined by:
- Nonterminal symbols (variables): Represent abstract categories or placeholders
(e.g., E,SE,S).
- Terminal symbols (alphabet): The actual characters or tokens in the language
(e.g., a, b,+,∗,(,)a, b, +, *, (, )a, b,+,∗,(,)).
- Production rules: Specify how non terminals can be replaced with other non terminals or terminals
(e.g., E→E+EE → E + EE→E+E).
- Start symbol: A special nonterminal from which derivations begin.
CFG vs. Other Models
| Model | Description |
|---|
| Finite Automata | Accept strings via computation (accept/reject). |
| Regular Expressions | Match strings by describing their structure. |
| CFG | Generate strings via recursive replacement. |
Example: Arithmetic Expressions
Suppose we want to describe all legal arithmetic expressions using addition, subtraction, multiplication, and division.
Here is one possible :
Production Rules:
CFG:
E → int
E → E Op E
E → (E)
Op → +
Op → -
Op → *
Op → /
Example Derivation:
E
⇒ E Op E
⇒ E Op int
⇒ int Op int
⇒ int / int
Designing a CFG
When creating CFGs:
- Base case: Define the simplest valid strings.
- Recursive rules: Combine smaller components into larger ones.
Examples:
1. Palindromes over {a, b}:
S → ε | a | b | aSa | bSb
2. Balanced Parentheses:
S → ε | (S) | SS
Languages Defined by CFGs
The language L(G) generated by a CFG G is: L(G)={ ω∈Σ*∣S⇒∗ω}
- ω: Strings made of terminals.
- S⇒∗ω: S derives ω via zero or more production applications.
Regular Languages vs. Context-Free Languages
| Property | Regular Languages | Context-Free Languages |
|---|
| Power | Limited | More expressive |
| Memory Requirements | Finite | Unbounded recursion |
| Definable Structures | Simple patterns (e.g., repetition) | Nested structures (e.g., palindromes, balanced parentheses) |
Non-CFG Example
Productions such as:
a->bSa, or
a->ba is not a CFG as on the left-hand side there is a terminal which does not follow the CFGs rule.
But we can construct it by :
Lets consider the string "aba" and and try to derive the given grammar from the productions given. We start with symbol S, apply production rule S->bSa and then (S->a) to get the string "aba".
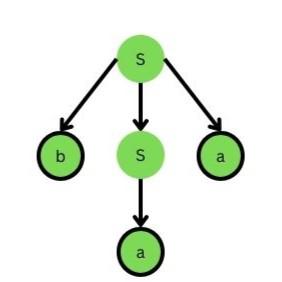 Parse tree of string "aba"
Parse tree of string "aba"In the computer science field, context-free grammars are frequently used, especially in the areas of formal language theory, compiler development, and natural language processing. It is also used for explaining the syntax of programming languages and other formal languages.
Limitations of Context-Free Grammar
- Cannot Handle Everything :
- CFGs are good for defining basic rules of a language, but they can’t handle everything.
- Some rules in English or programming languages are too complex for CFG.
- Can Be Confusing (Ambiguity)
- Sometimes, CFG can allow more than one meaning for the same sentence or code.
- This is called ambiguity, and it makes it hard for the computer to understand the correct meaning.
- Can’t Check Meaning
- CFGs only look at the structure, not the meaning.
- They can’t check if the types match, if variables are used properly, or if functions are called correctly.
21. Introduction to Context Free Grammars in TOC
Visit Course

Explore
Automata _ Introduction
Regular Expression and Finite Automata
CFG
PDA (Pushdown Automata)
Introduction of Pushdown Automata
5 min read
Pushdown Automata Acceptance by Final State
4 min read
Construct Pushdown Automata for given languages
4 min read
Construct Pushdown Automata for all length palindrome
6 min read
Detailed Study of PushDown Automata
3 min read
NPDA for accepting the language L = {anbm cn | m,n>=1}
2 min read
NPDA for accepting the language L = {an bn cm | m,n>=1}
2 min read
NPDA for accepting the language L = {anbn | n>=1}
2 min read
NPDA for accepting the language L = {amb2m| m>=1}
2 min read
NPDA for accepting the language L = {am bn cp dq | m+n=p+q ; m,n,p,q>=1}
2 min read
Construct Pushdown automata for L = {0n1m2m3n | m,n ≥ 0}
3 min read
Construct Pushdown automata for L = {0n1m2n+m | m, n ≥ 0}
2 min read
NPDA for accepting the language L = {ambncm+n | m,n ≥ 1}
2 min read
NPDA for accepting the language L = {amb(m+n)cn| m,n ≥ 1}
3 min read
NPDA for accepting the language L = {a2mb3m|m>=1}
2 min read
NPDA for accepting the language L = {amb2m+1 | m ≥ 1}
2 min read
NPDA for accepting the language L = {aibjckdl | i==k or j==l,i>=1,j>=1}
3 min read
Construct Pushdown automata for L = {a2mc4ndnbm | m,n ≥ 0}
3 min read
NPDA for L = {0i1j2k | i==j or j==k ; i , j , k >= 1}
2 min read
NPDA for accepting the language L = {anb2n| n>=1} U {anbn| n>=1}
2 min read
NPDA for the language L ={wЄ{a,b}* | w contains equal no. of a's and b's}
3 min read
Turing Machine
Decidability
TOC Interview preparation
TOC Quiz and PYQ's in TOC