Count Pairs from Two BSTs Whose Sum is Equal to a Given Value X in C++

We are given two binary search trees as input and a variable x. The goal is to find pairs of nodes from each tree such that the sum of value of nodes is equal to x. Take node 1 from BST_1 and node 2 from BST_2 and add data part of both. If sum=x. Increment count.

Let us understand with examples.

Input 

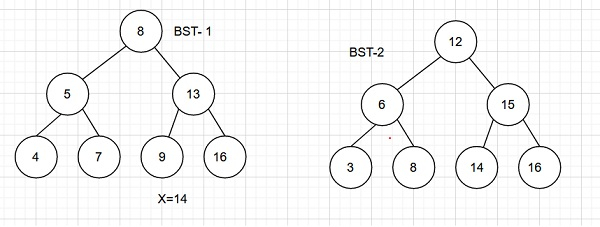
Output − Count of pairs from two BSTs whose sum is equal to a given value x are − 1

Explanation − The pair is (8,6)

Input 

Output −Count of pairs from two BSTs whose sum is equal to a given value x are − 2

Explanation − The pairs are (5,15) and (4,16)

Approach used in the below program is as follows

In this approach we will traverse the BST’s using an iterative inorder method. Traverse BST 1 from smallest node to largest using iterative inorder method and traverse BST 2 from reverse of iterative inorder method. Take the sum of current nodes of both BST’s. If sum is x increment count. If sum>x then move to the inorder predecessor of the current node in BST 2. If sum<x then move to the inorder predecessor of the current node in BST 1.

• Take two trees BST_1 and BST_2 having integer data part and left, right pointers to child nodes.

• Function insert_node(int data) inserts a new node to the Tree with data and returns a pointer to it.

• Create both BSTs using inser_node() and pass to BST_sum_x(Tree* BST_1, Tree* BST_2, int x).

• Function BST_sum_x(Tree* BST_1, Tree* BST_2, int x) takes root nodes of both trees and returns the count of pairs of nodes with sum of data part as x.

• Take the initial count as 0 for the number of pairs with sum x.

• For iterative inorder traversals take two variables Tree* stack_top_1, *stack_top_2;

• Create two stacks stack stack_1, stack_2;

• Now start outer while loop.

• Go to leftmost (smallest) node of BST_1 using while loop and push all nodes to stack_1

• Go to rightmost (greatest) node of BST_2 using while loop and push all nodes to stack_2

• If any of the stacks is empty break the outer while loop.

• Take the top nodes of both stacks and add their data parts and store in temp.

• If temp ( sum) == x then increment count. Remove top elements from both stack_1 and stack_2 using pop operation.

• Set BST_1=stack_1->right and BST_2=stack_2->left ( next successor in BST_1 and predecessor in BST_2 )

• If temp<x then only remove top from stack_1 and move to the next successor in BST_1.

• IF temp>x then only remove top from stack_2 and move to the next predecessor in BST_1.

• At the end of outer while, count has a number of pairs with node’s of both BSTs having sum x.

• Return count as result.

Example

 Live Demo

#include <bits/stdc++.h>
using namespace std;
struct Tree{
   int data;
   Tree* left, *right;
};
Tree* insert_node(int data){
   Tree* newNode = (Tree*)malloc(sizeof(Tree));
   newNode->data = data;
   newNode->left = NULL;
   newNode->right = NULL;
}
int BST_sum_x(Tree* BST_1, Tree* BST_2, int x){
   int count = 0;
   Tree* stack_top_1, *stack_top_2;
   stack<Tree*> stack_1, stack_2;
   if (BST_1 == NULL || BST_2 == NULL){
      return 0;
   }
   while (1){
      while (BST_1 != NULL){
         stack_1.push(BST_1);
         BST_1 = BST_1->left;
      }
      while (BST_2 != NULL){
         stack_2.push(BST_2);
         BST_2 = BST_2->right;
      }
      if (stack_1.empty() || stack_2.empty()){
         break;
      }
      stack_top_1 = stack_1.top();
      stack_top_2 = stack_2.top();
      int temp = stack_top_1->data + stack_top_2->data;
      if (temp == x){
         count++;
         stack_1.pop();
         stack_2.pop();
         BST_1 = stack_top_1->right;
         BST_2 = stack_top_2->left;
      }
      else if (temp < x){
         stack_1.pop();
         BST_1 = stack_top_1->right;
      }
      else{
         stack_2.pop();
         BST_2 = stack_top_2->left;
      }
   }
   return count;
}
int main(){
   //BST 1
   Tree* BST_1 = insert_node(15);
   BST_1->left = insert_node(10);
   BST_1->right = insert_node(8);
   BST_1->left->left = insert_node(12);
   BST_1->left->right = insert_node(24);
   BST_1->right->left = insert_node(16);
   //BST 2
   Tree* BST_2 = insert_node(20);
   BST_2->left = insert_node(16);
   BST_2->right = insert_node(4);
   BST_2->left->left = insert_node(18);
   BST_2->left->right = insert_node(28);
   BST_2->right->left = insert_node(22);
   int x = 28;
   cout<<"Count of pairs from two BSTs whose sum is equal to a given value x ar: "<<BST_sum_x(BST_1, BST_2, x);
   return 0;
}

Output

If we run the above code it will generate the following output −

Count of pairs from two BSTs whose sum is equal to a given value x ar: 1