What Is the Dummy Variable Trap? (With Pandas Code Examples)

Handling categorical variables forms an essential component of a machine learning pipeline. While machine learning algorithms can handle the numerical variables, the same is not true for their categorical counterparts. Although there are algorithms like LightGBM and Catboost that can inherently handle the categorical variables, this isn’t the case with most other algorithms. You have to first convert these categorical variables into numerical quantities to be fed into the machine learning algorithms. 

There are many ways to encode categorical variables, such as one-hot encoding, ordinal encoding and label encoding. In this article, I’ll look at Pandas’ dummy variable encoding and expose its potential limitations. 

What Is the Dummy Variable Trap?

The dummy variable trap is a multicollinearity problem that introduces redundant information when indicator variables are created. These variables, often called “dummy” variables, represent categorical data in regression analysis. However if used broadly, they can introduce linear dependency and make it difficult to interpret the individual effect of a summary variable on a prediction model.  

Let’s say we want to use the given data to build a machine learning model that can predict employees’ monthly salaries. This is a classic example of a regression problem where the target variable is MonthlyIncome. If we were to use pandas.get_dummies() to encode the categorical variables, we might run into the dummy variable trap. 

For example, if a Gender variable is used, the column would be split into Gender_Female and Gender_male. Because they are perfectly inversely related, including both violates the assumption of independence among the predictor variables. This multicollinearity can distort the model’s coefficient estimates and make interpretation unreliable.

Understanding Categorical Variables

Categorical variables are variables that have value ranges over categories, such as gender, hair color, ethnicity or zip codes. Since most algorithms can’t process non-numeric categories, dummy variables in turn translate their value into 0s and 1s so the model can interpret them. For example, when analyzing zip codes, per say, the sum of two zip codes is not meaningful. Similarly, nobody is asking for the average of a list of zip codes; that doesn’t make sense. Instead, categorical variables can be divided into two subcategories based on the kind of elements they group:

Nominal variables

are those whose categories do not have a natural order or ranking. For example, we could use 1 for the red color and 2 for blue. But these numbers don’t have a mathematical meaning. That is, we can’t add them together or take the average. Examples that fit in this category include gender, postal codes and hair color.

Ordinal variables

have an inherent order which is somehow significant. An example would be tracking student grades where Grade 1 > Grade 2 > Grade 3. Another example would be the socio-economic status of people where “high income” > “low income”.

How pandas.get_dummies Works

The Pandas library contains the function get_dummies() which converts categorical variables into dummy variables. The function uses one-hot encoding to transform each category into a new column with a binary value. 

Encoding Categorical Variables With pandas.get_dummies()

To use categorical variables directly in machine learning models they have to be converted into meaningful numerical representations; this process is called encoding. There are a lot of techniques for encoding categorical variables, but we’ll look at the one provided by the Pandas library called get_dummies().

As the name suggests, the pandas.get_dummies() function converts categorical variables into dummy or indicator variables. Let’s see it working through an elementary example. We first define a hypothetical data set consisting of employee attributes at a company and use it to predict employees’ salaries.

df = pd.DataFrame({
   'Gender' : ['Female', 'Male', 'Male', 'Male', 'Male', 'Female', 'Male', 'Male','Male', 'Female','Male', 'Female'],
   'Age' : [41, 49, 37, 33, 27, 32, 59, 30, 38, 36, 35, 29],
   'EducationField': ['Life Sciences', 'Engineering', 'Life Sciences', 'Life Sciences', 'Medical', 'Life Sciences', 'Life Sciences', 'Life Sciences', 'Engineering', 'Medical', 'Life Sciences', 'Life Sciences'],
   'MonthlyIncome': [5993, 5130, 2090, 2909, 3468, 3068, 2670, 2693, 9526, 5237, 2426, 4193]

 Our data set looks like this:

df

We can see that there are two categorical columns in the above data set (i.e., Gender and EducationField. Let’s encode them into numerical quantities using pandas.get_dummies() which returns a dummy-encoded data frame.

pd.get_dummies(df)

The column Gender gets converted into two columns: Gender_Female and Gender_Male having values as either zero or one. For instance, Gender_Female has a value = 1 at places where the concerned employee is female and value = 0 when not. The inverse is true for the column Gender_Male.

Similarly, the column EducationField also gets separated into three different columns based on the field of education. Things are pretty self-explanatory up until now. However, the issue begins when we use this encoded data set to train a machine learning model.

Common Dummy Variable Traps in Pandas

Trap 1: Multicollinearity

One of the assumptions of a regression model is that the observations must be independent of each other. Multicollinearity occurs when independent variables in a regression model are correlated. So why is correlation a problem? To help you understand the concept in detail and avoid reinventing the wheel, I’ll point you to a great piece by Jim Frost, where he explains it very succinctly. As Frost states,  “a key goal of regression analysis is to isolate the relationship between each independent variable and the dependent variable. The interpretation of a regression coefficient is that it represents the mean change in the dependent variable for each one unit change in an independent variable when you hold all of the other independent variables constant.”

If all the variables are correlated, it will become difficult for the model to tell how strongly a particular variable affects the target since all the variables are related. In such a case, the coefficient of a regression model will not convey the correct information.

The Help You Need From Built In ExpertsHow to Find Variance Using Python

Multicollinearity With pandas.get_dummies

Consider the employee example above. Let’s isolate the Gender column from the data set and encode it.

# Original categorical Gender data
Gender = ['Female', 'Male', 'Male', 'Male', 'Male', 'Male', 'Female',
          'Male', 'Male', 'Female', 'Male', 'Female']

# Dummy variable encoding for Gender
Gender_Female = [1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1]
Gender_Male   = [0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0]

If we look closely, Gender_Female and Gender_Male columns are multicollinear. This is because a value of 1 in one column automatically implies 0 in the other. We call this issue a dummy variable trap, which we  represent as:

Gender_Female = 1 - Gender_Male

Trap 2: Mismatched Columns Between Train and Test Sets

To train a model with the given employee data, we’ll first split the data set into train and test sets, keeping the test set aside so our model never sees it.

from sklearn.model_selection import train_test_split
X = df.drop('MonthlyIncome', axis=1)
y = df['MonthlyIncome']
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=1)

Encoding the Training Set

pd.get_dummies(X_train)

As expected, both the Gender and the EducationField attributes have been encoded into numerical quantities. Now we’ll apply the same process to the test data set.

Encoding the Test Set

pd.get_dummies(X_test)

Wait! There is a column mismatch in the training and test set. This means the number of columns in the training set is not equal to the ones in the test set, and this will introduce an error in the modeling process.

 

How to Avoid the Dummy Variable Trap

Below are a few common methods to avoid the dummy variable trap. 

Drop the First Column

Multicollinearity is undesirable, and every time we encode variables with pandas.get_dummies(), we’ll encounter this issue. One way to overcome this problem is by dropping one of the generated columns. So, we can drop either Gender_Female or Gender_Male without potentially losing any information. Fortunately, pandas.get_dummies() has a parameter called drop_first which, when set to True, does precisely that.

pd.get_dummies(df, drop_first=True

We’ve resolved multicollinearity, but another issue lurks when we use dummy_encoding.

Handle Unknown by Using .reindex and .fillna()

One way of addressing this categorical mismatch is to save the columns obtained after dummy encoding the training set in a list. Then, encode the test set as usual and use the columns of the encoded training set to align both the datas set. Let’s understand it through code:

# Dummy encoding Training set
X_train_encoded = pd.get_dummies(X_train)
# Saving the columns in a list
cols = X_train_encoded.columns.tolist()
# Viewing the first three rows of the encoded dataframe
X_train_encoded[:3]

Now, we’ll encode the test set followed by realigning the training and test columns and filling in all missing values with zero.

X_test_encoded = pd.get_dummies(X_test)
X_test_encoded = X_test_encoded.reindex(columns=cols).fillna(0)
X_test_encoded

As you can see, both data sets now have the same number of columns.

Use One-Hot Encoding

Another more preferable solution is to use sklearn.preprocessing.OneHotEncoder(). Additionally, one can use handle_unknown=“ignore” to solve the potential issues due to rare categories.

#One hot encoding the categorical columns in training set
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder(sparse=False, handle_unknown='ignore')
train_enc = ohe.fit_transform(X_train[['Gender','EducationField']])
#Converting back to a dataframe
pd.DataFrame(train_enc, columns=ohe.get_feature_names())[:3]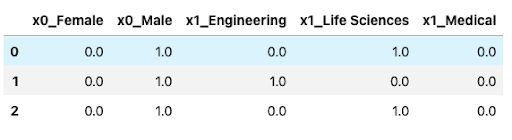

# Transforming the test set
test_enc = ohe.fit_transform(X_test[['Gender','EducationField']])
#Converting back to a dataframe
pd.DataFrame(test_enc,columns=ohe.get_feature_names())

Note, you can also drop one of the categories per feature in one- hot encoder by setting the parameter drop=’if_binary’. Refer to the documentation for more details.

OneHotEncoder vs get_dummies: Which Should You Use?

Both OneHotEncoder and get_dummies convert categorical features into numeric features that can be processed by an algorithm. However, they each take a unique approach. Most notably, get_dummies does not handle unknown categories, which can cause mismatches between training and test data, potentially leading to errors of broken pipelines during model inference. In contrast, OneHotEncoder handles unknown categories by assigning them all-zero vectors, thereby retaining consistent columns between training and test datasets. 

Because of their differences, data scientists often use get_dummies for fast prototyping or exploratory data analysis, whereas OneHotEncoder is better suited for production-ready machine learning pipelines. 

Frequently Asked Questions