Rotate an Array - Clockwise or Right
Rotations in the array is defined as the process of rearranging the elements in an array by shifting each element to a new position. This is mostly done by rotating the elements of the array clockwise or counterclockwise.
Table of Content
Types of Rotations in Array
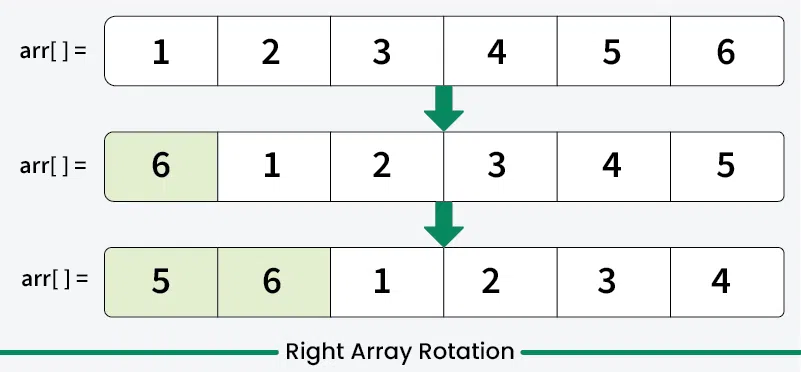
1. Right Rotation (or Clockwise)
Here, The array elements are shifted towards the right.
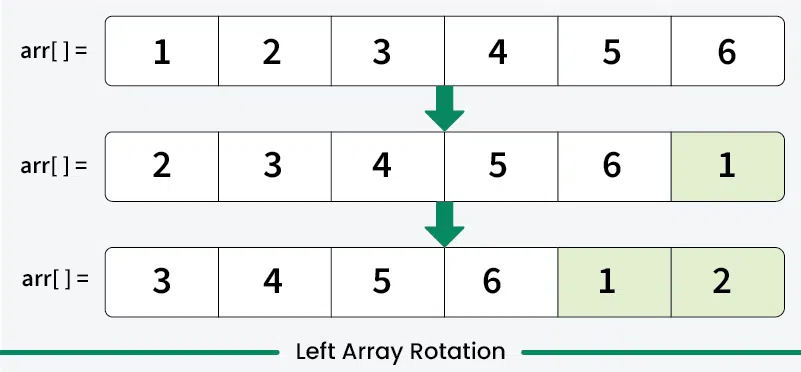
2. Left Rotation (Or Counter Clockwise)
Here, The array elements are shifted towards the left.
In this article, we will discuss about right rotation of the array. You can refer to Left rotate an array by d positions to know about the left rotation of the array.
How to implement rotations in an array?
There are several ways to implement array rotations. Some of the approaches are mentioned below. Here we are considering right rotation. The movements will be just the opposite for left rotation.
Input: arr[] = {1, 2, 3, 4, 5, 6}, d = 2
Output: {5, 6, 1, 2, 3, 4}
Explanation: After first right rotation, arr[] becomes {6, 1, 2, 3, 4, 5} and after the second rotation, arr[] becomes {5, 6, 1, 2, 3, 4}Input: arr[] = {1, 2, 3}, d = 4
Output: {3, 1, 2}
Explanation: The array is rotated as follows:
- After first left rotation, arr[] = {3, 1, 2}
- After second left rotation, arr[] = {2, 3, 1}
- After third left rotation, arr[] = {1, 2, 3}
- After fourth left rotation, arr[] = {3, 1, 2}
1. Rotate one by one
At each iteration, shift the elements by one position to the right in a circular fashion (the last element becomes the first). Perform this operation d times to rotate the elements to the right by d positions.
Illustration:
Let us take arr[] = {1, 2, 3, 4, 5, 6}, d = 2.
First Step:
=> Rotate to right by one position.
=> arr[] = {6, 1, 2, 3, 4, 5}
Second Step:
=> Rotate again to right by one position
=> arr[] = {5, 6, 1, 2, 3, 4}
Rotation is done 2 times.
So the array becomes arr[] = {5, 6, 1, 2, 3, 4}
// C++ Program to right rotate the array by d positions
// by rotating one element at a time
#include <bits/stdc++.h>
using namespace std;
// Function to right rotate array by d positions
void rotateArr(vector<int>& arr, int d) {
int n = arr.size();
// Repeat the rotation d times
for (int i = 0; i < d; i++) {
// Right rotate the array by one position
int last = arr[n - 1];
for (int j = n - 1; j > 0; j--) {
arr[j] = arr[j - 1];
}
arr[0] = last;
}
}
int main() {
vector<int> arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
return 0;
}
// C Program to right rotate the array by d positions
// by rotating one element at a time
#include <stdio.h>
// Function to right rotate array by d positions
void rotateArr(int arr[], int n, int d) {
// Repeat the rotation d times
for (int i = 0; i < d; i++) {
// Right rotate the array by one position
int last = arr[n - 1];
for (int j = n - 1; j > 0; j--) {
arr[j] = arr[j - 1];
}
arr[0] = last;
}
}
int main() {
int arr[] = { 1, 2, 3, 4, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
int d = 2;
rotateArr(arr, n, d);
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}
// Java Program to right rotate the array by d positions
// by rotating one element at a time
import java.util.Arrays;
class GfG {
// Function to right rotate array by d positions
static void rotateArr(int[] arr, int d) {
int n = arr.length;
// Repeat the rotation d times
for (int i = 0; i < d; i++) {
// Right rotate the array by one position
int last = arr[n - 1];
for (int j = n - 1; j > 0; j--) {
arr[j] = arr[j - 1];
}
arr[0] = last;
}
}
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
# Python Program to right rotate the array by d positions
# by rotating one element at a time
# Function to right rotate array by d positions
def rotateArr(arr, d):
n = len(arr)
# Repeat the rotation d times
for _ in range(d):
# Right rotate the array by one position
last = arr[n - 1]
for i in range(n - 1, 0, -1):
arr[i] = arr[i - 1]
arr[0] = last
if __name__ == "__main__":
arr = [1, 2, 3, 4, 5, 6]
d = 2
rotateArr(arr, d)
# Print the rotated array
for i in range(len(arr)):
print(arr[i], end=" ")
// C# Program to right rotate the array by d positions
// by rotating one element at a time
using System;
class GfG {
// Function to right rotate array by d positions
static void rotateArr(int[] arr, int d) {
int n = arr.Length;
// Repeat the rotation d times
for (int i = 0; i < d; i++) {
// Right rotate the array by one position
int last = arr[n - 1];
for (int j = n - 1; j > 0; j--)
arr[j] = arr[j - 1];
arr[0] = last;
}
}
static void Main() {
int[] arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
// Print the rotated array
for (int i = 0; i < arr.Length; i++) {
Console.Write(arr[i] + " ");
}
Console.WriteLine();
}
}
// JavaScript Program to right rotate the array by d positions
// by rotating one element at a time
// Function to right rotate array by d positions
function rotateArr(arr, d) {
let n = arr.length;
// Repeat the rotation d times
for (let i = 0; i < d; i++) {
// Right rotate the array by one position
let last = arr[n - 1];
for (let j = n - 1; j > 0; j--)
arr[j] = arr[j - 1];
arr[0] = last;
}
}
let arr = [1, 2, 3, 4, 5, 6];
let d = 2;
rotateArr(arr, d);
console.log(arr.join(' '));
Output
5 6 1 2 3 4
Time Complexity: O(n * d)
Auxiliary Space: O(1)
2. Using Temporary Array
The idea is to use a temporary array of size n, where n is the length of the original array. If we right rotate the array by d positions, the last d elements will be in the beginning and the first (n - d) elements will be at the end.
- Copy the last d elements of the original array into the first d positions of the temporary array
- Then copy the first n - d elements of the original array to the end of temporary array.
- Finally, copy all the elements of temporary array back into the original array.
Illustration for Right Rotation by 2 positions:








Below is the implementation of the above approach
// C++ Program to right rotate the array by d positions
// using temporary array
#include <bits/stdc++.h>
using namespace std;
// Function to rotate vector
void rotateArr(vector<int>& arr, int d) {
int n = arr.size();
// Handle case when d > n
d %= n;
// Storing rotated version of array
vector<int> temp(n);
// Copy last d elements to the front of temp
for (int i = 0; i < d; i++)
temp[i] = arr[n - d + i];
// Copy the first n - d elements to the back of temp
for (int i = 0; i < n - d; i++)
temp[i + d] = arr[i];
// Copying the elements of temp in arr
// to get the final rotated vector
for (int i = 0; i < n; i++)
arr[i] = temp[i];
}
int main() {
vector<int> arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
// Print the rotated vector
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
return 0;
}
// C Program to right rotate the array by d positions
// using temporary array
#include <stdio.h>
#include <stdlib.h>
// Function to rotate array by d positions using a temporary array
void rotateArr(int arr[], int n, int d) {
// Handle case when d > n
d %= n;
// Storing rotated version of array
int temp[n];
// Copy last d elements to the front of temp
for (int i = 0; i < d; i++)
temp[i] = arr[n - d + i];
// Copy the first n - d elements to the back of temp
for (int i = 0; i < n - d; i++)
temp[i + d] = arr[i];
// Copying the elements of temp in arr to get the
// final rotated array
for (int i = 0; i < n; i++)
arr[i] = temp[i];
}
int main() {
int arr[] = { 1, 2, 3, 4, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
int d = 2;
rotateArr(arr, n, d);
// Print the rotated array
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}
// Java Program to right rotate the array by d positions
// using temporary array
import java.util.Arrays;
class GfG {
// Function to rotate array by d positions using a temporary array
static void rotateArr(int[] arr, int d) {
int n = arr.length;
// Handle case when d > n
d %= n;
// Storing rotated version of array
int[] temp = new int[n];
// Copy last d elements to the front of temp
for (int i = 0; i < d; i++)
temp[i] = arr[n - d + i];
// Copy the first n - d elements to the back of temp
for (int i = 0; i < n - d; i++)
temp[i + d] = arr[i];
// Copying the elements of temp in arr to get the
// final rotated array
for (int i = 0; i < n; i++)
arr[i] = temp[i];
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6};
int d = 2;
rotateArr(arr, d);
// Print the rotated array
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
# Python Program to right rotate the array by d positions
# using temporary array
def rotateArr(arr, d):
n = len(arr)
# Handle case when d > n
d %= n
# Storing rotated version of array
temp = [0] * n
# Copy last d elements to the front of temp
for i in range(d):
temp[i] = arr[n - d + i]
# Copy the first n - d elements to the back of temp
for i in range(n - d):
temp[i + d] = arr[i]
# Copying the elements of temp in arr
# to get the final rotated array
for i in range(n):
arr[i] = temp[i]
if __name__ == "__main__":
arr = [1, 2, 3, 4, 5, 6]
d = 2
rotateArr(arr, d)
# Print the rotated array
print(' '.join(map(str, arr)))
// C# Program to right rotate the array by d positions
// using temporary array
using System;
class GfG {
// Function to rotate array
static void rotateArr(int[] arr, int d) {
int n = arr.Length;
// Handle case when d > n
d %= n;
// Storing rotated version of array
int[] temp = new int[n];
// Copy last d elements to the front of temp
for (int i = 0; i < d; i++)
temp[i] = arr[n - d + i];
// Copy the first n - d elements to the back of temp
for (int i = 0; i < n - d; i++)
temp[i + d] = arr[i];
// Copying the elements of temp in arr
// to get the final rotated array
for (int i = 0; i < n; i++)
arr[i] = temp[i];
}
static void Main() {
int[] arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
// Print the rotated array
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
}
// JavaScript Program to right rotate the array by d positions
// using temporary array
// Function to rotate array
function rotateArr(arr, d) {
let n = arr.length;
// Handle case when d > n
d %= n;
// Storing rotated version of array
let temp = new Array(n);
// Copy last d elements to the front of temp
for (let i = 0; i < d; i++) {
temp[i] = arr[n - d + i];
}
// Copy the first n - d elements to the back of temp
for (let i = 0; i < n - d; i++) {
temp[i + d] = arr[i];
}
// Copying the elements of temp in arr
// to get the final rotated array
for (let i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
let arr = [1, 2, 3, 4, 5, 6];
let d = 2;
rotateArr(arr, d);
// Print the rotated array
console.log(arr.join(' '));
Output
5 6 1 2 3 4
Time complexity: O(n), where n is the size of input array arr[].
Auxiliary Space: O(n)
3. Juggling Algorithm
The idea behind Juggling Algorithm is that instead of moving one by one, we can use the concept of cycles. Each cycle is independent and represents a group of elements that will shift among themselves during the rotation. If the starting index of a cycle is i, then the next elements will be present at indices (i + d) % n, (i + 2d) % n, (i + 3d) % n ... and so on till we reach back to index i.
So for any index i, we know that element at index i will move to index (i + d) % n. Now, we can simply rotate all elements in the same cycle without interfering with any other cycle.
Working of the above algorithm:
















Below is the implementation of the algorithm:
// C++ Program to right rotate the array by d positions
// using Juggling Algorithm
#include <bits/stdc++.h>
using namespace std;
// Function to rotate vector
void rotateArr(vector<int> &arr, int d) {
int n = arr.size();
// Handle the case where d > size of array
d %= n;
// Calculate the number of cycles in the rotation
int cycles = __gcd(n, d);
// Process each cycle
for (int i = 0; i < cycles; i++) {
// Start index of current cycle
int currIdx = i;
int currEle = arr[currIdx];
// Rotate elements till we reach the start of cycle
do {
int nextIdx = (currIdx + d) % n;
int nextEle = arr[nextIdx];
// Update the element at next index with the current element
arr[nextIdx] = currEle;
// Update the current element to next element
currEle = nextEle;
// Move to the next index
currIdx = nextIdx;
} while (currIdx != i);
}
}
int main()
{
vector<int> arr = {1, 2, 3, 4, 5, 6};
int d = 2;
rotateArr(arr, d);
// Print the rotated vector
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
return 0;
}
// C Program to right rotate the array by d positions
// using Juggling Algorithm
#include <stdio.h>
#include <stdlib.h>
// Function to rotate array
void rotateArr(int *arr, int n, int d) {
// Handle the case where d > size of array
d %= n;
// Calculate the number of cycles in the rotation
int cycles = gcd(n, d);
// Process each cycle
for (int i = 0; i < cycles; i++) {
// Start index of current cycle
int currIdx = i;
int currEle = arr[currIdx];
// Rotate elements till we reach the start of cycle
do {
int nextIdx = (currIdx + d) % n;
int nextEle = arr[nextIdx];
// Update the element at next index with the current element
arr[nextIdx] = currEle;
// Update the current element to next element
currEle = nextEle;
// Move to the next index
currIdx = nextIdx;
} while (currIdx != i);
}
}
// function to compute GCD
int gcd(int a, int b) {
while (b) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
int main() {
int arr[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
int d = 2;
rotateArr(arr, n, d);
// Print the rotated array
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}
// Java Program to right rotate the array by d positions
// using Juggling Algorithm
import java.util.Arrays;
class GfG {
// Function to rotate array
static void rotateArr(int[] arr, int d) {
int n = arr.length;
// Handle the case where d > size of array
d %= n;
// Calculate the number of cycles in the rotation
int cycles = gcd(n, d);
// Process each cycle
for (int i = 0; i < cycles; i++) {
// Start index of current cycle
int currIdx = i;
int currEle = arr[currIdx];
// Rotate elements till we reach the start of cycle
do {
int nextIdx = (currIdx + d) % n;
int nextEle = arr[nextIdx];
// Update the element at next index with the current element
arr[nextIdx] = currEle;
// Update the current element to next element
currEle = nextEle;
// Move to the next index
currIdx = nextIdx;
} while (currIdx != i);
}
}
// function to compute GCD
public static int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6};
int d = 2;
rotateArr(arr, d);
// Print the rotated array
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " ");
}
}
# Java Program to right rotate the array by d positions
# using Juggling Algorithm
from math import gcd
# Function to rotate list
def rotateArr(arr, d):
n = len(arr)
# Handle the case where d > size of array
d %= n
# Calculate the number of cycles in the rotation
cycles = gcd(n, d)
# Process each cycle
for i in range(cycles):
# Start index of current cycle
currIdx = i
currEle = arr[currIdx]
# Rotate elements till we reach the start of cycle
while True:
nextIdx = (currIdx + d) % n
nextEle = arr[nextIdx]
# Update the element at next index with the current element
arr[nextIdx] = currEle
# Update the current element to next element
currEle = nextEle
# Move to the next index
currIdx = nextIdx
if currIdx == i:
break
if __name__ == "__main__":
arr = [1, 2, 3, 4, 5, 6]
d = 2
rotateArr(arr, d)
# Print the rotated list
for i in range(len(arr)):
print(arr[i], end=" ")
// C# Program to right rotate the array by d positions
// using Juggling Algorithm
using System;
class GfG {
// Function to rotate array
static void RotateArr(int[] arr, int d) {
int n = arr.Length;
// Handle the case where d > size of array
d %= n;
// Calculate the number of cycles in the rotation
int cycles = Gcd(n, d);
// Process each cycle
for (int i = 0; i < cycles; i++) {
// Start index of current cycle
int currIdx = i;
int currEle = arr[currIdx];
// Rotate elements till we reach the start of cycle
do {
int nextIdx = (currIdx + d) % n;
int nextEle = arr[nextIdx];
// Update the element at next index with the current element
arr[nextIdx] = currEle;
// Update the current element to next element
currEle = nextEle;
// Move to the next index
currIdx = nextIdx;
} while (currIdx != i);
}
}
// function to compute GCD
static int Gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
static void Main(string[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
RotateArr(arr, d);
// Print the rotated array
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
}
}
// JavaScript Program to right rotate the array by d positions
// using Juggling Algorithm
// Function to rotate array
function rotateArr(arr, d) {
const n = arr.length;
// Handle the case where d > size of array
d %= n;
// Calculate the number of cycles in the rotation
const cycles = gcd(n, d);
// Process each cycle
for (let i = 0; i < cycles; i++) {
// Start index of current cycle
let currIdx = i;
let currEle = arr[currIdx];
// Rotate elements till we reach the start of cycle
do {
let nextIdx = (currIdx + d) % n;
let nextEle = arr[nextIdx];
// Update the element at next index with the current element
arr[nextIdx] = currEle;
// Update the current element to next element
currEle = nextEle;
// Move to the next index
currIdx = nextIdx;
} while (currIdx !== i);
}
}
// function to compute GCD
function gcd(a, b) {
while (b !== 0) {
const temp = b;
b = a % b;
a = temp;
}
return a;
}
const arr = [1, 2, 3, 4, 5, 6];
const d = 2;
rotateArr(arr, d);
// Print the rotated array
console.log(arr.join(" "));
Output
5 6 1 2 3 4
4. The Reversal Algorithm
The idea is based on the observation that if we right rotate the array by d positions, the last d elements will be in the front and first (n - d) elements will be at the end.
- First reverse all the elements of the array.
- Then reverse first d elements.
- Finally, reverse last (n - d) elements to get the final rotated array.
Illustration:








Below is the implementation of the above approach:
// C++ Code to right rotate an array using Reversal Algorithm
#include <bits/stdc++.h>
using namespace std;
// Function to rotate an array by d elements to the right
void rotateArr(vector<int>& arr, int d) {
int n = arr.size();
// Handle the case where d > size of array
d %= n;
// Reverse the entire array
reverse(arr.begin(), arr.end());
// Reverse the first d elements
reverse(arr.begin(), arr.begin() + d);
// Reverse the remaining n-d elements
reverse(arr.begin() + d, arr.end());
}
int main() {
vector<int> arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
return 0;
}
// C Code to right rotate an array using Reversal Algorithm
#include <stdio.h>
// Function to reverse a portion of the array from start to end
void reverse(int arr[], int start, int end) {
while (start < end) {
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
// Function to rotate an array by d elements to the right
void rotateArr(int arr[], int n, int d) {
// Handle the case where d > size of array
d %= n;
// Reverse the entire array
reverse(arr, 0, n - 1);
// Reverse the first d elements
reverse(arr, 0, d - 1);
// Reverse the remaining n-d elements
reverse(arr, d, n - 1);
}
int main() {
int arr[] = { 1, 2, 3, 4, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
int d = 2;
rotateArr(arr, n, d);
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}
// Java Code to right rotate an array using Reversal Algorithm
import java.util.*;
class GfG {
// Function to rotate an array by d elements to the right
static void rotateArr(int[] arr, int d) {
int n = arr.length;
// Handle the case where d > size of array
d %= n;
// Reverse the entire array
reverse(arr, 0, n - 1);
// Reverse the first d elements
reverse(arr, 0, d - 1);
// Reverse the remaining n-d elements
reverse(arr, d, n - 1);
}
// function to reverse a portion of the array
static void reverse(int[] arr, int start, int end) {
while (start < end) {
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " ");
}
}
# Python Code to right rotate an array using Reversal Algorithm
# Function to rotate an array by d elements to the right
def rotateArr(arr, d):
n = len(arr)
# Handle the case where d > size of array
d %= n
# Reverse the entire array
arr.reverse()
# Reverse the first d elements
arr[:d] = reversed(arr[:d])
# Reverse the remaining n-d elements
arr[d:] = reversed(arr[d:])
if __name__ == "__main__":
arr = [1, 2, 3, 4, 5, 6]
d = 2
rotateArr(arr, d)
for i in range(len(arr)):
print(arr[i], end=" ")
// C# Code to right rotate an array using Reversal Algorithm
using System;
class GfG {
// Function to rotate an array by d elements to the right
static void rotateArr(int[] arr, int d) {
int n = arr.Length;
// Handle the case where d > size of array
d %= n;
// Reverse the entire array
Array.Reverse(arr);
// Reverse the first d elements
Array.Reverse(arr, 0, d);
// Reverse the remaining n-d elements
Array.Reverse(arr, d, n - d);
}
static void Main() {
int[] arr = { 1, 2, 3, 4, 5, 6 };
int d = 2;
rotateArr(arr, d);
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
}
}
// JavaScript Code to right rotate an array using Reversal Algorithm
// Function to rotate an array by d elements to the right
function rotateArr(arr, d) {
let n = arr.length;
// Handle the case where d > size of array
d %= n;
// Reverse the entire array
arr.reverse();
// Reverse the first d elements
reverse(arr, 0, d - 1);
// Reverse the remaining n-d elements
reverse(arr, d, n - 1);
}
// function to reverse a portion of the array
function reverse(arr, start, end) {
while (start < end) {
let temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
let arr = [1, 2, 3, 4, 5, 6];
let d = 2;
rotateArr(arr, d);
console.log(arr.join(" "));
Output
5 6 1 2 3 4
Time Complexity: O(n)
Auxiliary Space: O(1)
- Program for array left rotation by d positions
- Find the Rotation Count in Rotated Sorted array
- Maximum sum of i*arr[i] among all rotations of a given array
- Find the Minimum element in a Sorted and Rotated Array
- Quickly find multiple left rotations of an array