Top MCQs on Queue Data Structure with Answers
Question 2
Consider the following statements:
i. First-in-first out types of computations are efficiently supported by STACKS.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
Which of the following is correct?
(ii) is true
(i) and (ii) are true
(iii) is true
(ii) and (iv) are true
Question 3
A queue is implemented using a non-circular singly linked list. The queue has a head pointer and a tail pointer, as shown in the figure. Let n denote the number of nodes in the queue. Let 'enqueue' be implemented by inserting a new node at the head, and 'dequeue' be implemented by deletion of a node from the tail.
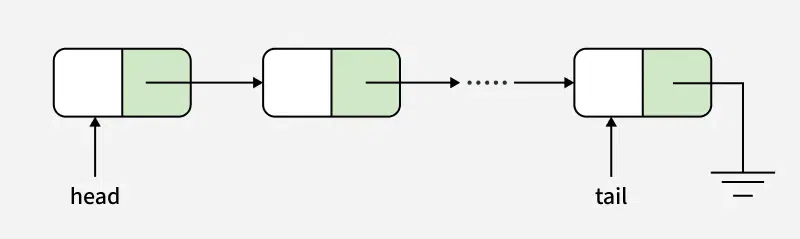
Which one of the following is the time complexity of the most time-efficient implementation of 'enqueue' and 'dequeue, respectively, for this data structure?
Θ(1), Θ(1)
Θ(1), Θ(n)
Θ(n), Θ(1)
Θ(n), Θ(n)
Question 4
Circular queue is also called -----.
Ring Buffer
Rectangular Buffer
Square Buffer
None
Question 5
Given a queue with a linked list implementation. the Rear pointer points to the rear node of the queue. and the front node of the queue points to the front node of the queue, Which of the following operations is impossible to do in O(1) time?
Delete the front item from the list.
Delete the rear from the list.
insert at the front of the list.
None
Question 6
What is wrong in the below code of printing Right View of a binary tree using the Queue data structure?
#include <iostream>
#include <queue>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int val) : data(val), left(nullptr), right(nullptr) {}
};
void printRightView(Node* root) {
if (root == nullptr) return;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int n = q.size();
for (int i = 0; i < n; i++) {
Node* x = q.front();
q.pop();
if (i == n - 1) {
cout << x->data << " ";
}
if (x->left) {
q.push(x->left);
}
if (x->right) {
q.push(x->right);
}
}
}
}
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* left;
struct Node* right;
};
void printRightView(struct Node* root) {
if (root == NULL) return;
struct Node** queue = (struct Node**)malloc(100 * sizeof(struct Node*));
int front = 0, rear = 0;
queue[rear++] = root;
while (front < rear) {
int n = rear - front;
for (int i = 0; i < n; i++) {
struct Node* x = queue[front++];
if (i == n - 1) {
printf("%d ", x->data);
}
if (x->left) {
queue[rear++] = x->left;
}
if (x->right) {
queue[rear++] = x->right;
}
}
}
free(queue);
}
import java.util.LinkedList;
import java.util.Queue;
class Node {
int data;
Node left, right;
Node(int val) {
data = val;
left = right = null;
}
}
public class Main {
public static void printRightView(Node root) {
if (root == null) return;
Queue<Node> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
int n = q.size();
for (int i = 0; i < n; i++) {
Node x = q.poll();
if (i == n - 1) {
System.out.print(x.data + " ");
}
if (x.left != null) {
q.add(x.left);
}
if (x.right != null) {
q.add(x.right);
}
}
}
}
}
from collections import deque
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def printRightView(root):
if root is None:
return
q = deque([root])
while q:
n = len(q)
for i in range(n):
x = q.popleft()
if i == n - 1:
print(x.data, end=' ')
if x.left:
q.append(x.left)
if x.right:
q.append(x.right)
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function printRightView(root) {
if (root === null) return;
let q = [root];
while (q.length) {
let n = q.length;
for (let i = 0; i < n; i++) {
let x = q.shift();
if (i === n - 1) {
process.stdout.write(x.data + ' ');
}
if (x.left) q.push(x.left);
if (x.right) q.push(x.right);
}
}
}
We have not initialized anything in the Queue
Queue will never be empty.
left and right nodes of the tree are null.
None
Question 7
Which of the following is the type of priority Queue?
Ascending Order Priority Queue
Descending order Priority Queue
Deque
Both A and B.
Question 8
which data structure is used to implement deque?
Stack
Doubly linked list
circular array
Both B and C
Question 9
Which of the following is/are advantages of circular Queue?
Memory Management
Traffic system
CPU Scheduling
All of the above
Question 10
Consider the below program, and identify what the function is doing.
#include <iostream>
#include <queue>
class Node {
public:
int data;
Node* left;
Node* right;
Node(int item) {
data = item;
left = right = nullptr;
}
};
void function(Node* root) {
if (root == nullptr)
return;
std::queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* node = q.front();
q.pop();
std::cout << node->data << " ";
if (node->left != nullptr)
q.push(node->left);
if (node->right != nullptr)
q.push(node->right);
}
}
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int item) {
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->data = item;
node->left = node->right = NULL;
return node;
}
void function(struct Node* root) {
if (root == NULL)
return;
struct Node** q = (struct Node**)malloc(100 * sizeof(struct Node*));
int front = 0, rear = 0;
q[rear++] = root;
while (front < rear) {
struct Node* node = q[front++];
printf("%d ", node->data);
if (node->left != NULL)
q[rear++] = node->left;
if (node->right != NULL)
q[rear++] = node->right;
}
free(q);
}
import java.util.LinkedList;
import java.util.Queue;
class Node {
int data;
Node left, right;
Node(int item) {
data = item;
left = right = null;
}
}
void function(Node root) {
if (root == null)
return;
Queue<Node> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
Node node = q.poll();
System.out.print(node.data + " ");
if (node.left != null)
q.add(node.left);
if (node.right != null)
q.add(node.right);
}
}
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
from collections import deque
def function(root):
if root is None:
return
q = deque()
q.append(root)
while q:
node = q.popleft()
print(node.data, end=' ')
if node.left is not None:
q.append(node.left)
if node.right is not None:
q.append(node.right)
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function function(root) {
if (root === null)
return;
let q = [];
q.push(root);
while (q.length > 0) {
let node = q.shift();
console.log(node.data);
if (node.left !== null)
q.push(node.left);
if (node.right !== null)
q.push(node.right);
}
}
In order traversal of a tree
Normal traversal of a tree
Level order traversal of a tree
None
There are 30 questions to complete.