Difference between NP hard and NP complete problem
Last Updated :
25 Feb, 2025
All NP Complete Problems are NP-Hard but vice versa is not true. NP-Complete problems are subset of NP Problems.
NP Problems : NP problems are a class of computational problems that can be solved in polynomial time by a non-deterministic machine and can be verified in polynomial time by a deterministic Machine (our CPUs are deterministic machines). As we can see in the below diagram, NP set also includes P problems (Problems that solvable in polynomial time by a deterministic machine).
NP Complete Problems : A decision problem is NP-complete if it is in NP (Any solution to NP-complete problems can be checked quickly, but no efficient solution is known) and every problem in NP is reducible to it in polynomial time
NP Hard : A problem is NP-Hard if it obeys Property 2 (all NP problems can be reduced to it) of NP Complete and need not obey Property 1 (It is in NP).
Therefore, a problem is NP-complete if it is both NP and NP-hard.
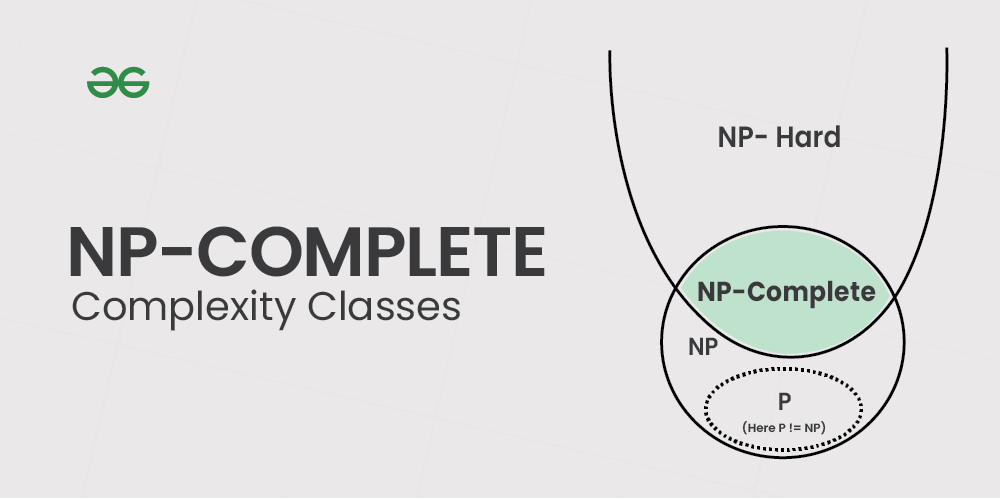
Difference between NP-Hard and NP-Complete:
| NP-hard | NP-Complete |
|---|
| Polynomial time verification by a deterministic machine is not necessary. | Can be verified in Polynomial time by a deterministic machine. |
| NP-hard is not a decision problem. | NP-Complete is exclusively a decision problem. |
| Not all NP-hard problems are NP-complete. | All NP-complete problems are NP-hard |
| Do not have to be a Decision problem. | It is exclusively a Decision problem. |
Need not to be a NP problem | Must be NP |
| Example: Halting problem, Vertex cover problem, etc. | Example: Determine whether a graph has a Hamiltonian cycle, Determine whether a Boolean formula is satisfiable or not, Circuit-satisfiability problem and problems that are NP hard. |
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem