Introduction to Binary Tree

Binary Tree is a non-linear and hierarchical data structure where each node has at most two children referred to as the left child and the right child.  The topmost node in a binary tree is called the root, and the bottom-most nodes(having no children) are called leaves.

Representation of Binary Tree

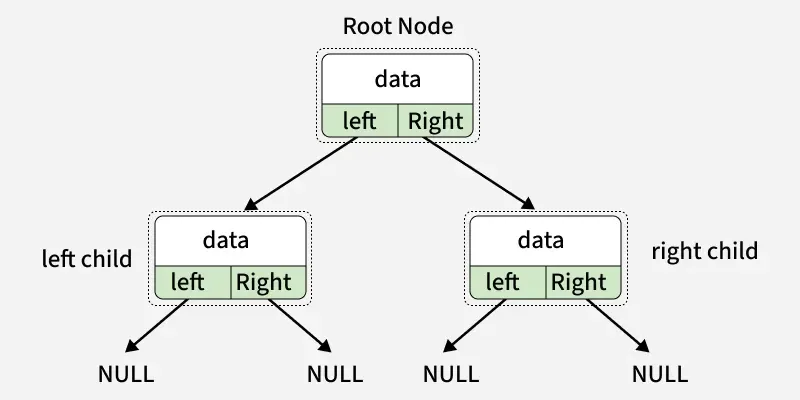
Each node in a Binary Tree has three parts:

• Data
• Pointer to the left child
• Pointer to the right child

Terminologies in Binary Tree

• Parent Node: A node that is the direct ancestor of a node(its child node).
• Child Node: A node that is the direct descendant of another node (its parent).
• Ancestors of a node: All nodes on the path from the root to that node (including the node itself).
• Descendants of a node: All nodes that lie in the subtree rooted at that node (including the node itself).
• Subtree of a node: A tree consisting of that node as root and all its descendants.
• Edge: The link/connection between a parent node and its child node.
• Path in a binary tree: A sequence of nodes connected by edges from one node to another.
• Leaf Node: A node that does not have any children or both children are null.
• Internal Node: A node that has at least one child.
• Depth/Level of a Node: The number of edges in the path from root to that node. The depth/level of the root node is zero.
• Height of a Binary Tree: The number of edges on the longest path from root to a leaf.

The diagram below shows all these terms in a binary tree.

Create/Declare a Node of a Binary Tree

Syntax to declare a Node of Binary Tree in different languages:

// Node structure
class Node {
public:
    int data;
    Node* left, * right;

    Node(int key) {
        data = key;
        left = nullptr;
        right = nullptr;
    }
};

// Structure of each node of the tree. 
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

// Note : Unlike other languages, C does not support 
// Object Oriented Programming. So we need to write 
// a separat method for create and instance of tree node
struct Node* newNode(int item) {
    struct Node* temp = 
       (struct Node*)malloc(sizeof(struct Node));
    temp->key = item;
    temp->left = temp->right = NULL;
    return temp;
}

// Node structure
class Node {
    int key;
    Node left, right;
    public Node(int item)
    {
        key = item;
        left = right = null;
    }
}

# Node structure
class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key

// Node structure
class Node {
    int key;
    Node left, right;

    public Node(int item)
    {
        key = item;
        left = right = null;
    }
}

// Node structure
class Node
{
    constructor(item)
    {
        this.data = item;
        this.left = this.right = null;
    }
}

Creating a Binary Tree

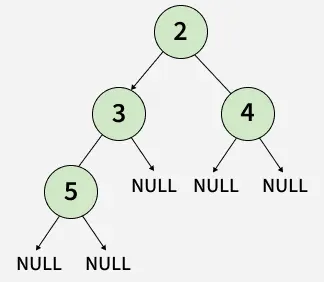
In this example, we will explore how to create a Binary Tree with four nodes 2, 3, 4, 5.

#include <iostream>
using namespace std;

// Node structure
class Node {
public:
    int data;
    Node* left, * right;

    Node(int key) {
        data = key;
        left = nullptr;
        right = nullptr;
    }
};

int main(){
    // Initilize and allocate memory for tree nodes
    Node* firstNode = new Node(2);
    Node* secondNode = new Node(3);
    Node* thirdNode = new Node(4);
    Node* fourthNode = new Node(5);

    // Connect binary tree nodes
    firstNode->left = secondNode;
    firstNode->right = thirdNode;
    secondNode->left = fourthNode;
    return 0;
}

#include <stdio.h>
#include <stdlib.h>

// Node structure
struct Node {
    int data;
    struct Node *left;
    struct Node *right;
};

struct Node* createNode(int d) {
    struct Node* newNode =
      (struct Node*)malloc(sizeof(struct Node));
    newNode->data = d;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

int main() {
    // Initialize and allocate memory for tree nodes
    struct Node* firstNode = createNode(2);
    struct Node* secondNode = createNode(3);
    struct Node* thirdNode = createNode(4);
    struct Node* fourthNode = createNode(5);

    // Connect binary tree nodes
    firstNode->left = secondNode;
    firstNode->right = thirdNode;
    secondNode->left = fourthNode;

    return 0;
}

// Node structure
class Node {
    int data;
    Node left, right;
    Node(int d) {
        data = d;
        left = null;
        right = null;
    }
}

class GfG {
    public static void main(String[] args) {
        // Initialize and allocate memory for tree nodes
        Node firstNode = new Node(2);
        Node secondNode = new Node(3);
        Node thirdNode = new Node(4);
        Node fourthNode = new Node(5);

        // Connect binary tree nodes
        firstNode.left = secondNode;
        firstNode.right = thirdNode;
        secondNode.left = fourthNode;

    }
}

# Node structure
class Node:
    def __init__(self, d):
        self.data = d
        self.left = None
        self.right = None

# Initialize and allocate memory for tree nodes
firstNode = Node(2)
secondNode = Node(3)
thirdNode = Node(4)
fourthNode = Node(5)

# Connect binary tree nodes
firstNode.left = secondNode
firstNode.right = thirdNode
secondNode.left = fourthNode

using System;

// Node structure
class Node {
    public int data;
    public Node left, right;

    public Node(int d) {
        this.data = d;
        left = null;
        right = null;
    }
}

class GfG {
    static void Main() {
        // Initialize and allocate memory for tree nodes
        Node firstNode = new Node(2);
        Node secondNode = new Node(3);
        Node thirdNode = new Node(4);
        Node fourthNode = new Node(5);

        // Connect binary tree nodes
        firstNode.left = secondNode;
        firstNode.right = thirdNode;
        secondNode.left = fourthNode;
    }
}

// Node structure
class Node {
    constructor(d) {
        this.data = d;
        this.left = null;
        this.right = null;
    }
}

// Initialize and allocate memory for tree nodes
let firstNode = new Node(2);
let secondNode = new Node(3);
let thirdNode = new Node(4);
let fourthNode = new Node(5);

// Connect binary tree nodes
firstNode.left = secondNode;
firstNode.right = thirdNode;
secondNode.left = fourthNode;

In the above code, we have created four tree nodes firstNode, secondNode, thirdNode and fourthNode with values 2, 3, 4 and 5 respectively, and then established links between those nodes wrt the given tree structure.

Properties of Binary Tree

• The maximum number of nodes at level L of a binary tree is 2^L.
• The maximum number of nodes in a binary tree of height H is 2^H+1 – 1.
• Total number of leaf nodes in a binary tree = total number of nodes with 2 children + 1.
• In a Binary Tree with N nodes, the minimum possible height or the minimum number of levels is ⌊log₂N⌋.
• A Binary Tree with L leaves has at least ⌈log₂L⌉+ 1 levels.

Please refer Properties of Binary Tree for more details.

Operations On Binary Tree

Following is a list of common operations that can be performed on a binary tree:

1. Traversal: Depth-First Search (DFS) Traversal and Breadth-First Search (BFS) Traversal
2. Search: Search a node in Binary Tree
3. Insertion and Deletion: Prerequisite: Level Order Traversal, Insert in a Binary Tree and Delete from a Binary Tree

Advantages of Binary Tree

• Efficient Search: Binary Search Trees (a variation of Binary Tree) are efficient when searching for a specific element, as each node has at most two child nodes when compared to linked list and arrays
• Memory Efficient: Binary trees require lesser memory as compared to other tree data structures, therefore memory-efficient.
• Binary trees are relatively easy to implement and understand as each node has at most two children, left child and right child.

Disadvantages of Binary Tree

• Limited structure: Binary trees are limited to two child nodes per node, which can limit their usefulness in certain applications. For example, if a tree requires more than two child nodes per node, a different tree structure may be more suitable.
• Space inefficiency: Binary trees can be space inefficient when compared to other data structures like arrays and linked list. This is because each node requires two child references or pointers, which can be a significant amount of memory overhead for large trees.

Applications of Binary Tree

• Binary Tree can be used to represent hierarchical data.
• Huffman Coding trees are used in data compression algorithms.
• Useful for indexing segmented at the database is useful in storing cache in the system,
• Binary trees can be used to implement decision trees, a type of machine learning algorithm used for classification and regression analysis.