Introduction to Min-Heap – Data Structure and Algorithm Tutorials
Last Updated :
23 Jul, 2025
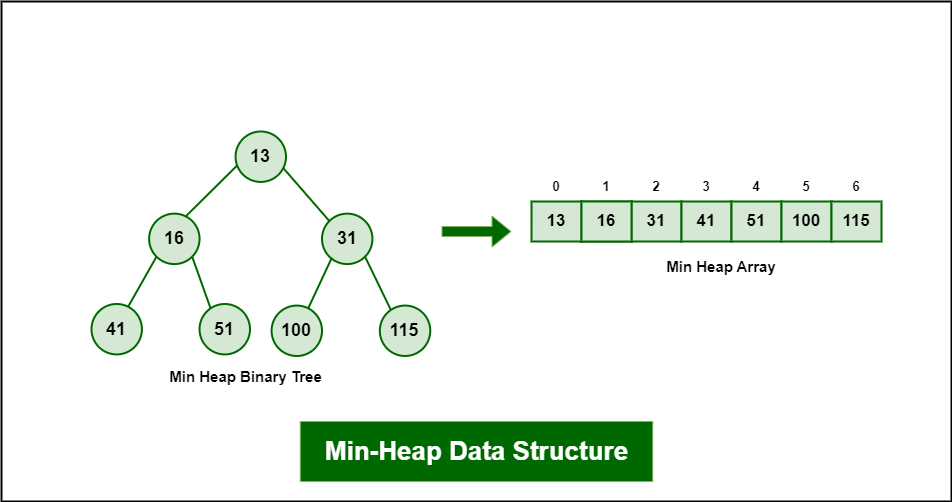
A Min-Heap is a Data Structure with the following properties.
- It is a complete Complete Binary Tree.
- The value of the root node must be the smallest among all its descendant nodes and the same thing must be done for its left and right sub-tree also.
Use Cases of Min-Heap:
- Implementing Priority Queue: One of the primary uses of the heap data structure is for implementing priority queues.
- Huffman Coding : Lossless compression algorithm.
- Dijkstra's Algorithm: Dijkstra's algorithm is a shortest path algorithm that finds the shortest path between two nodes in a graph. A min heap can be used to keep track of the unvisited nodes with the smallest distance from the source node.
- Sorting: A min heap can be used as a sorting algorithm to efficiently sort a collection of elements in ascending order.
- Median finding: A min heap can be used to efficiently find the median of a stream of numbers. We can use one min heap to store the larger half of the numbers and one max heap to store the smaller half. The median will be the root of the min heap.
Min-Heap Data structure in Different languages:
C++
priority_queue < int, vector<int>, greater<int> > minH;
PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
var minHeap = new PriorityQueue<int>();
Internal Implementation of Min-Heap Data Structure
Mapping the elements of a heap into an array is trivial: if a node is stored an index k, then its left child is stored at index 2i + 1 and its right child at index 2i + 2.
.png)
A Min heap is typically represented as an array.
- The root element will be at arr[0].
- For any ith node arr[i]:
- arr[(i -1) / 2] returns its parent node.
- arr[(2 * i) + 1] returns its left child node.
- arr[(2 * i) + 2] returns its right child node.
The Internal Implementation of the Min-Heap requires 3 major steps:
- Insertion: To insert an element into the min heap, we first append the element to the end of the array and then adjust the heap property by repeatedly swapping the element with its parent until it is in the correct position.
- Deletion: To remove the minimum element from the min heap, we first swap the root node with the last element in the array, remove the last element, and then adjust the heap property by repeatedly swapping the element with its smallest child until it is in the correct position.
- Heapify: A heapify operation can be used to create a min heap from an unsorted array.
Operations on Min-heap Data Structure and their Implementation:
Here are some common operations that can be performed on a Heap Data Structure,
Insertion in Min-Heap Data Structure
Elements can be inserted into the heap following a similar approach as discussed above for deletion. The idea is to:
- The insertion operation in a min-heap involves the following steps:
- Add the new element to the end of the heap, in the next available position in the last level of the tree.
- Compare the new element with its parent. If the parent is greater than the new element, swap them.
- Repeat step 2 until the parent is smaller than or equal to the new element, or until the new element reaches the root of the tree.
- The new element is now in its correct position in the min heap, and the heap property is satisfied.
Illustration:
Suppose the Heap is a Min-Heap as:
Insertion in Min-Heap
Implementation of Insertion Operation in Min-Heap:
C++
#include <iostream>
#include <vector>
using namespace std;
// Function to insert a new element into the min-heap
void insert_min_heap(vector<int>& heap, int value)
{
// Add the new element to the end of the heap
heap.push_back(value);
// Get the index of the last element
int index = heap.size() - 1;
// Compare the new element with its parent and swap if
// necessary
while (index > 0
&& heap[(index - 1) / 2] > heap[index]) {
swap(heap[index], heap[(index - 1) / 2]);
// Move up the tree to the parent of the current
// element
index = (index - 1) / 2;
}
}
// Main function to test the insert_min_heap function
int main()
{
vector<int> heap;
int values[] = { 10, 7, 11, 5, 4, 13 };
int n = sizeof(values) / sizeof(values[0]);
for (int i = 0; i < n; i++) {
insert_min_heap(heap, values[i]);
cout << "Inserted " << values[i]
<< " into the min-heap: ";
for (int j = 0; j < heap.size(); j++) {
cout << heap[j] << " ";
}
cout << endl;
}
return 0;
}
import java.util.*;
public class GFG {
// Function to insert a new element into the min-heap
public static void insertMinHeap(int[] heap, int size,
int value)
{
// Add the new element to the end of the heap
heap[size] = value;
// Get the index of the last element
int index = size;
// Compare the new element with its parent and swap
// if necessary
while (index > 0
&& heap[(index - 1) / 2] > heap[index]) {
swap(heap, index, (index - 1) / 2);
// Move up the tree to the parent of the current
// element
index = (index - 1) / 2;
}
}
// Function to swap two elements in an array
public static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// Main function to test the insertMinHeap function
public static void main(String[] args)
{
int[] heap = new int[6];
int[] values = { 10, 7, 11, 5, 4, 13 };
int size = 0;
for (int i = 0; i < values.length; i++) {
insertMinHeap(heap, size, values[i]);
size++;
System.out.print("Inserted " + values[i]
+ " into the min-heap: ");
for (int j = 0; j < size; j++) {
System.out.print(heap[j] + " ");
}
System.out.println();
}
}
}
def insert_min_heap(heap, value):
# Add the new element to the end of the heap
heap.append(value)
# Get the index of the last element
index = len(heap) - 1
# Compare the new element with its parent and swap if necessary
while index > 0 and heap[(index - 1) // 2] > heap[index]:
heap[index], heap[(index - 1) //
2] = heap[(index - 1) // 2], heap[index]
# Move up the tree to the parent of the current element
index = (index - 1) // 2
heap = []
values = [10, 7, 11, 5, 4, 13]
for value in values:
insert_min_heap(heap, value)
print(f"Inserted {value} into the min-heap: {heap}")
using System;
using System.Collections.Generic;
public class Program {
// Function to insert a new element into the min-heap
static void InsertMinHeap(List<int> heap, int value)
{
// Add the new element to the end of the heap
heap.Add(value);
// Get the index of the last element
int index = heap.Count - 1;
// Compare the new element with its parent and swap
// if necessary
while (index > 0
&& heap[(index - 1) / 2] > heap[index]) {
int temp = heap[index];
heap[index] = heap[(index - 1) / 2];
heap[(index - 1) / 2] = temp;
// Move up the tree to the parent of the current
// element
index = (index - 1) / 2;
}
}
// Main function to test the InsertMinHeap function
public static void Main()
{
List<int> heap = new List<int>();
int[] values = { 10, 7, 11, 5, 4, 13 };
foreach(int value in values)
{
InsertMinHeap(heap, value);
Console.Write("Inserted " + value
+ " into the min-heap: ");
foreach(int element in heap)
{
Console.Write(element + " ");
}
Console.WriteLine();
}
}
}
function insertMinHeap(heap, value) {
heap.push(value);
let index = heap.length - 1;
let parentIndex = Math.floor((index - 1) / 2);
while (index > 0 && heap[parentIndex] > heap[index]) {
[heap[index], heap[parentIndex]] = [heap[parentIndex], heap[index]];
index = parentIndex;
parentIndex = Math.floor((index - 1) / 2);
}
}
// Example usage
const heap = [];
const values = [10, 7, 11, 5, 4, 13];
for (const value of values) {
insertMinHeap(heap, value);
console.log(`Inserted ${value} into the min-heap: ${heap}`);
}
OutputInserted 10 into the min-heap: 10
Inserted 7 into the min-heap: 7 10
Inserted 11 into the min-heap: 7 10 11
Inserted 5 into the min-heap: 5 7 11 10
Inserted 4 into the min-heap: 4 5 11 10 7
Inser...
Time Complexity: O(log(n)) (where n is no of elements in the heap)
Auxiliary Space: O(n)
Deletion in Min-Heap Data Structure
Removing the smallest element (the root) from the min heap. The root is replaced by the last element in the heap, and then the heap property is restored by swapping the new root with its smallest child until the parent is smaller than both children or until the new root reaches a leaf node.
- Replace the root or element to be deleted with the last element.
- Delete the last element from the Heap.
- Since the last element is now placed at the position of the root node. So, it may not follow the heap property. Therefore, heapify the last node placed at the position of the root.
Illustration:
Implementation of Deletion operation in Min-Heap:
C++
#include <iostream>
#include <vector>
using namespace std;
// Function to insert a new element into the min-heap
void insert_min_heap(vector<int>& heap, int value)
{
// Add the new element to the end of the heap
heap.push_back(value);
// Get the index of the last element
int index = heap.size() - 1;
// Compare the new element with its parent and swap if
// necessary
while (index > 0
&& heap[(index - 1) / 2] > heap[index]) {
swap(heap[index], heap[(index - 1) / 2]);
// Move up the tree to the parent of the current
// element
index = (index - 1) / 2;
}
}
// Function to delete a node from the min-heap
void delete_min_heap(vector<int>& heap, int value)
{
// Find the index of the element to be deleted
int index = -1;
for (int i = 0; i < heap.size(); i++) {
if (heap[i] == value) {
index = i;
break;
}
}
// If the element is not found, return
if (index == -1) {
return;
}
// Replace the element to be deleted with the last
// element
heap[index] = heap[heap.size() - 1];
// Remove the last element
heap.pop_back();
// Heapify the tree starting from the element at the
// deleted index
while (true) {
int left_child = 2 * index + 1;
int right_child = 2 * index + 2;
int smallest = index;
if (left_child < heap.size()
&& heap[left_child] < heap[smallest]) {
smallest = left_child;
}
if (right_child < heap.size()
&& heap[right_child] < heap[smallest]) {
smallest = right_child;
}
if (smallest != index) {
swap(heap[index], heap[smallest]);
index = smallest;
}
else {
break;
}
}
}
// Main function to test the insert_min_heap and
// delete_min_heap functions
int main()
{
vector<int> heap;
int values[] = { 13, 16, 31, 41, 51, 100 };
int n = sizeof(values) / sizeof(values[0]);
for (int i = 0; i < n; i++) {
insert_min_heap(heap, values[i]);
}
cout << "Initial heap: ";
for (int j = 0; j < heap.size(); j++) {
cout << heap[j] << " ";
}
cout << endl;
delete_min_heap(heap, 13);
cout << "Heap after deleting 13: ";
for (int j = 0; j < heap.size(); j++) {
cout << heap[j] << " ";
}
cout << endl;
return 0;
}
import java.util.*;
public class GFG {
// Function to insert a new element into the min-heap
public static void insertMinHeap(List<Integer> heap,
int value)
{
// Add the new element to the end of the heap
heap.add(value);
// Get the index of the last element
int index = heap.size() - 1;
// Compare the new element with its parent and swap
// if necessary
while (index > 0
&& heap.get((index - 1) / 2)
> heap.get(index)) {
Collections.swap(heap, index, (index - 1) / 2);
// Move up the tree to the parent of the current
// element
index = (index - 1) / 2;
}
}
// Function to delete a node from the min-heap
public static void deleteMinHeap(List<Integer> heap,
int value)
{
// Find the index of the element to be deleted
int index = -1;
for (int i = 0; i < heap.size(); i++) {
if (heap.get(i) == value) {
index = i;
break;
}
}
// If the element is not found, return
if (index == -1) {
return;
}
// Replace the element to be deleted with the last
// element
heap.set(index, heap.get(heap.size() - 1));
// Remove the last element
heap.remove(heap.size() - 1);
// Heapify the tree starting from the element at the
// deleted index
while (true) {
int leftChild = 2 * index + 1;
int rightChild = 2 * index + 2;
int smallest = index;
if (leftChild < heap.size()
&& heap.get(leftChild)
< heap.get(smallest)) {
smallest = leftChild;
}
if (rightChild < heap.size()
&& heap.get(rightChild)
< heap.get(smallest)) {
smallest = rightChild;
}
if (smallest != index) {
Collections.swap(heap, index, smallest);
index = smallest;
}
else {
break;
}
}
}
// Main function to test the insertMinHeap and
// deleteMinHeap functions
public static void main(String[] args)
{
List<Integer> heap = new ArrayList<Integer>();
int[] values = { 13, 16, 31, 41, 51, 100 };
int n = values.length;
for (int i = 0; i < n; i++) {
insertMinHeap(heap, values[i]);
}
System.out.print("Initial heap: ");
for (int j = 0; j < heap.size(); j++) {
System.out.print(heap.get(j) + " ");
}
System.out.println();
deleteMinHeap(heap, 13);
System.out.print("Heap after deleting 13: ");
for (int j = 0; j < heap.size(); j++) {
System.out.print(heap.get(j) + " ");
}
System.out.println();
}
}
def insert_min_heap(heap, value):
heap.append(value)
index = len(heap) - 1
while index > 0 and heap[(index - 1) // 2] > heap[index]:
heap[index], heap[(index - 1) //
2] = heap[(index - 1) // 2], heap[index]
index = (index - 1) // 2
def delete_min_heap(heap, value):
index = -1
for i in range(len(heap)):
if heap[i] == value:
index = i
break
if index == -1:
return
heap[index] = heap[-1]
heap.pop()
while True:
left_child = 2 * index + 1
right_child = 2 * index + 2
smallest = index
if left_child < len(heap) and heap[left_child] < heap[smallest]:
smallest = left_child
if right_child < len(heap) and heap[right_child] < heap[smallest]:
smallest = right_child
if smallest != index:
heap[index], heap[smallest] = heap[smallest], heap[index]
index = smallest
else:
break
heap = []
values = [13, 16, 31, 41, 51, 100]
for value in values:
insert_min_heap(heap, value)
print("Initial heap:", heap)
delete_min_heap(heap, 13)
print("Heap after deleting 13:", heap)
using System;
using System.Collections.Generic;
class MinHeap {
private List<int> heap = new List<int>();
public void Insert(int value)
{
heap.Add(value);
int index = heap.Count - 1;
while (index > 0
&& heap[(index - 1) / 2] > heap[index]) {
Swap(index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
public void Delete(int value)
{
int index = heap.IndexOf(value);
if (index == -1) {
return;
}
heap[index] = heap[heap.Count - 1];
heap.RemoveAt(heap.Count - 1);
while (true) {
int leftChild = 2 * index + 1;
int rightChild = 2 * index + 2;
int smallest = index;
if (leftChild < heap.Count
&& heap[leftChild] < heap[smallest]) {
smallest = leftChild;
}
if (rightChild < heap.Count
&& heap[rightChild] < heap[smallest]) {
smallest = rightChild;
}
if (smallest != index) {
Swap(index, smallest);
index = smallest;
}
else {
break;
}
}
}
private void Swap(int i, int j)
{
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
public void Print()
{
for (int i = 0; i < heap.Count; i++) {
Console.Write(heap[i] + " ");
}
Console.WriteLine();
}
}
class Program {
static void Main(string[] args)
{
MinHeap heap = new MinHeap();
int[] values = { 13, 16, 31, 41, 51, 100 };
for (int i = 0; i < values.Length; i++) {
heap.Insert(values[i]);
}
Console.Write("Initial heap: ");
heap.Print();
heap.Delete(13);
Console.Write("Heap after deleting 13: ");
heap.Print();
}
}
function insertMinHeap(heap, value) {
// Add the new element to the end of the heap
heap.push(value);
// Get the index of the last element
let index = heap.length - 1;
// Compare the new element with its parent and swap if necessary
for (let flr = Math.floor((index - 1) / 2); index > 0 && heap[flr] > heap[index]; flr = Math.floor((index - 1) / 2)) {
[heap[index], heap[flr]] = [
heap[flr],
heap[index],
];
// Move up the tree to the parent of the current element
index = Math.floor((index - 1) / 2);
}
}
function deleteMinHeap(heap, value) {
// Find the index of the element to be deleted
let index = -1;
for (let i = 0; i < heap.length; i++) {
if (heap[i] == value) {
index = i;
break;
}
}
// If the element is not found, return
if (index == -1) {
return;
}
// Replace the element to be deleted with the last element
heap[index] = heap[heap.length - 1];
// Remove the last element
heap.pop();
// Heapify the tree starting from the element at the deleted index
while (true) {
let left_child = 2 * index + 1;
let right_child = 2 * index + 2;
let smallest = index;
if (left_child < heap.length && heap[left_child] < heap[smallest]) {
smallest = left_child;
}
if (right_child < heap.length && heap[right_child] < heap[smallest]) {
smallest = right_child;
}
if (smallest != index) {
[heap[index], heap[smallest]] = [heap[smallest], heap[index]];
index = smallest;
} else {
break;
}
}
}
// Main function to test the insertMinHeap and deleteMinHeap functions
let heap = [];
let values = [13, 16, 31, 41, 51, 100];
for (let i = 0; i < values.length; i++) {
insertMinHeap(heap, values[i]);
}
console.log("Initial heap: " + heap.join(" "));
deleteMinHeap(heap, 13);
console.log("Heap after deleting 13: " + heap.join(" "));
OutputInitial heap: 13 16 31 41 51 100
Heap after deleting 13: 16 41 31 100 51
Time complexity: O(log n) where n is no of elements in the heap
Auxiliary Space: O(n)
for more detail refer - Insertion and Deletion in Heaps
Peek operation on Min-Heap Data Structure
To access the minimum element (i.e., the root of the heap), the value of the root node is returned. The time complexity of peek in a min-heap is O(1).
Min Heap Data StructureImplementation of Peek operation in Min-Heap:
C++
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main()
{
// Create a max heap with some elements using a
// priority_queue
priority_queue<int, vector<int>, greater<int> > minHeap;
minHeap.push(9);
minHeap.push(8);
minHeap.push(7);
minHeap.push(6);
minHeap.push(5);
minHeap.push(4);
minHeap.push(3);
minHeap.push(2);
minHeap.push(1);
// Get the peak element (i.e., the largest element)
int peakElement = minHeap.top();
// Print the peak element
cout << "Peak element: " << peakElement << std::endl;
return 0;
}
import java.util.PriorityQueue;
public class GFG {
public static void main(String[] args)
{
// Create a max heap with some elements using a
// PriorityQueue
PriorityQueue<Integer> minHeap
= new PriorityQueue<>();
minHeap.add(9);
minHeap.add(8);
minHeap.add(7);
minHeap.add(6);
minHeap.add(5);
minHeap.add(4);
minHeap.add(3);
minHeap.add(2);
minHeap.add(1);
// Get the peak element (i.e., the largest element)
int peakElement = minHeap.peek();
// Print the peak element
System.out.println("Peak element: " + peakElement);
}
}
import heapq
# Create a min heap with some elements using a list
min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1]
heapq.heapify(min_heap)
# Get the peak element (i.e., the smallest element)
peak_element = heapq.nsmallest(1, min_heap)[0]
# Print the peak element
print("Peak element:", peak_element)
using System;
using System.Collections.Generic;
public class GFG {
public static void Main()
{
// Create a min heap with some elements using a
// PriorityQueue
var minHeap = new PriorityQueue<int>();
minHeap.Enqueue(9);
minHeap.Enqueue(8);
minHeap.Enqueue(7);
minHeap.Enqueue(6);
minHeap.Enqueue(5);
minHeap.Enqueue(4);
minHeap.Enqueue(3);
minHeap.Enqueue(2);
minHeap.Enqueue(1);
// Get the peak element (i.e., the smallest element)
int peakElement = minHeap.Peek();
// Print the peak element
Console.WriteLine("Peak element: " + peakElement);
}
}
const PriorityQueue = require('fast-priority-queue');
// Create a min heap with some elements using a PriorityQueue
const minHeap = new PriorityQueue((a, b) => a - b);
minHeap.add(9);
minHeap.add(8);
minHeap.add(7);
minHeap.add(6);
minHeap.add(5);
minHeap.add(4);
minHeap.add(3);
minHeap.add(2);
minHeap.add(1);
// Get the peak element (i.e., the smallest element)
const peakElement = minHeap.peek();
// Print the peak element
console.log(`Peak element: ${peakElement}`);
Time complexity: In a min heap implemented using an array or a list, the peak element can be accessed in constant time, O(1), as it is always located at the root of the heap.
In a min heap implemented using a binary tree, the peak element can also be accessed in O(1) time, as it is always located at the root of the tree.
Auxiliary Space: O(n)
Heapify operation on Min-Heap Data Structure
A heapify operation can be used to create a min heap from an unsorted array. This is done by starting at the last non-leaf node and repeatedly performing the "bubble down" operation until all nodes satisfy the heap property.
Heapify operation in Min HeapImplementation of Heapify operation in Min-Heap:
C++
#include <iostream>
#include <vector>
using namespace std;
void minHeapify(vector<int> &arr, int i, int n) {
int smallest = i;
int l = 2*i + 1;
int r = 2*i + 2;
if (l < n && arr[l] < arr[smallest])
smallest = l;
if (r < n && arr[r] < arr[smallest])
smallest = r;
if (smallest != i) {
swap(arr[i], arr[smallest]);
minHeapify(arr, smallest, n);
}
}
int main() {
vector<int> arr = {10, 5, 15, 2, 20, 30};
cout << "Original array: ";
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
// Perform heapify operation on min-heap
for (int i = arr.size()/2 - 1; i >= 0; i--)
minHeapify(arr, i, arr.size());
cout << "\nMin-Heap after heapify operation: ";
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
return 0;
}
// Java code of Heapify operation in Min-Heap
import java.util.Arrays;
import java.util.List;
public class Main {
// Function to maintain the min-heap property of the heap rooted at index 'i'
public static void minHeapify(List<Integer> arr, int i, int n) {
// Assume the root is the smallest element initially
int smallest = i;
// Calculate the indices of the left and right child of the current node
int l = 2 * i + 1;
int r = 2 * i + 2;
// Compare the left child with the current smallest
if (l < n && arr.get(l) < arr.get(smallest))
smallest = l;
// Compare the right child with the current smallest
if (r < n && arr.get(r) < arr.get(smallest))
smallest = r;
// If the current node is not the smallest, swap it with the smallest child
if (smallest != i) {
int temp = arr.get(i);
arr.set(i, arr.get(smallest));
arr.set(smallest, temp);
// Recursively heapify the subtree rooted at the smallest child
minHeapify(arr, smallest, n);
}
}
public static void main(String[] args) {
// Create a list representing the array
List<Integer> arr = Arrays.asList(10, 5, 15, 2, 20, 30);
System.out.print("Original array: ");
// Print the original array
for (int i = 0; i < arr.size(); i++)
System.out.print(arr.get(i) + " ");
// Perform heapify operation on the min-heap
// Start from the last non-leaf node and go up to the root of the tree
for (int i = arr.size() / 2 - 1; i >= 0; i--)
minHeapify(arr, i, arr.size());
System.out.print("\nMin-Heap after heapify operation: ");
// Print the min-heap after heapify operation
for (int i = 0; i < arr.size(); i++)
System.out.print(arr.get(i) + " ");
}
}
def minHeapify(arr, i, n):
smallest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and arr[left] < arr[smallest]:
smallest = left
if right < n and arr[right] < arr[smallest]:
smallest = right
if smallest != i:
arr[i], arr[smallest] = arr[smallest], arr[i]
minHeapify(arr, smallest, n)
if __name__ == "__main__":
arr = [10, 5, 15, 2, 20, 30]
print("Original array:", arr)
# Perform heapify operation on a min-heap
for i in range(len(arr) // 2 - 1, -1, -1):
minHeapify(arr, i, len(arr))
print("Min-Heap after heapify operation:", arr)
using System;
using System.Collections.Generic;
class GFG
{
// Function to perform the minHeapify operation on a min-heap.
static void MinHeapify(List<int> arr, int i, int n)
{
int smallest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Compare the left child with the current smallest node.
if (left < n && arr[left] < arr[smallest])
smallest = left;
// Compare the right child with the current smallest node.
if (right < n && arr[right] < arr[smallest])
smallest = right;
// If the current node is not the smallest
// swap it with the smallest child.
if (smallest != i)
{
int temp = arr[i];
arr[i] = arr[smallest];
arr[smallest] = temp;
// Recursively call minHeapify on the affected subtree.
MinHeapify(arr, smallest, n);
}
}
static void Main(string[] args)
{
List<int> arr = new List<int> { 10, 5, 15, 2, 20, 30 };
Console.Write("Original array: ");
foreach (int num in arr)
Console.Write(num + " ");
// Perform heapify operation on the min-heap.
for (int i = arr.Count / 2 - 1; i >= 0; i--)
MinHeapify(arr, i, arr.Count);
Console.Write("\nMin-Heap after heapify operation: ");
foreach (int num in arr)
Console.Write(num + " ");
}
}
// Define a function to perform min-heapify operation on an array
function minHeapify(arr, i, n) {
let smallest = i;
let l = 2 * i + 1;
let r = 2 * i + 2;
// Check if left child is smaller than the current smallest element
if (l < n && arr[l] < arr[smallest])
smallest = l;
// Check if right child is smaller than the current smallest element
if (r < n && arr[r] < arr[smallest])
smallest = r;
// If the smallest element is not the current element, swap them
if (smallest !== i) {
[arr[i], arr[smallest]] = [arr[smallest], arr[i]];
minHeapify(arr, smallest, n);
}
}
// Main function
function main() {
const arr = [10, 5, 15, 2, 20, 30];
// Print the original array
console.log("Original array: " + arr.join(" "));
// Perform heapify operation on the min-heap
for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--)
minHeapify(arr, i, arr.length);
// Print the min-heap after heapify operation
console.log("Min-Heap after heapify operation: " + arr.join(" "));
}
// Call the main function to start the process
main();
OutputOriginal array: 10 5 15 2 20 30
Min-Heap after heapify operation: 2 5 15 10 20 30
The time complexity of heapify in a min-heap is O(n).
Search operation on Min-Heap Data Structure
To search for an element in the min heap, a linear search can be performed over the array that represents the heap. However, the time complexity of a linear search is O(n), which is not efficient. Therefore, searching is not a commonly used operation in a min heap.
Here's an example code that shows how to search for an element in a min heap using std::find():
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
priority_queue<int, vector<int>, greater<int> >
min_heap;
// example max heap
min_heap.push(10);
min_heap.push(9);
min_heap.push(8);
min_heap.push(6);
min_heap.push(4);
int element = 6; // element to search for
bool found = false;
// Copy the min heap to a temporary queue and search for
// the element
std::priority_queue<int, vector<int>, greater<int> >
temp = min_heap;
while (!temp.empty()) {
if (temp.top() == element) {
found = true;
break;
}
temp.pop();
}
if (found) {
std::cout << "Element found in the min heap."
<< std::endl;
}
else {
std::cout << "Element not found in the min heap."
<< std::endl;
}
return 0;
}
import java.util.PriorityQueue;
public class GFG {
public static void main(String[] args)
{
PriorityQueue<Integer> min_heap
= new PriorityQueue<>();
min_heap.add(
3); // insert elements into the priority queue
min_heap.offer(1);
min_heap.offer(4);
min_heap.offer(1);
min_heap.offer(6);
int element = 6; // element to search for
boolean found = false;
// Copy the min heap to a temporary queue and search
// for the element
PriorityQueue<Integer> temp
= new PriorityQueue<>(min_heap);
while (!temp.isEmpty()) {
if (temp.poll() == element) {
found = true;
break;
}
}
if (found) {
System.out.println(
"Element found in the min heap.");
}
else {
System.out.println(
"Element not found in the min heap.");
}
}
}
import heapq
min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap
heapq.heapify(min_heap)
element = 6 # element to search for
found = False
# Copy the min heap to a temporary list and search for the element
temp = list(min_heap)
while temp:
if heapq.heappop(temp) == element:
found = True
break
if found:
print("Element found in the min heap.")
else:
print("Element not found in the min heap.")
using System;
using System.Collections.Generic;
public class GFG {
public static void Main()
{
var minHeap = new PriorityQueue<int>();
// example min heap
minHeap.Enqueue(4);
minHeap.Enqueue(6);
minHeap.Enqueue(8);
minHeap.Enqueue(9);
minHeap.Enqueue(10);
int element = 6; // element to search for
bool found = false;
// Copy the min heap to a temporary queue and search
// for the element
var temp = new PriorityQueue<int>(minHeap);
while (temp.Count > 0) {
if (temp.Peek() == element) {
found = true;
break;
}
temp.Dequeue();
}
if (found) {
Console.WriteLine(
"Element found in the min heap.");
}
else {
Console.WriteLine(
"Element not found in the min heap.");
}
}
}
// Example min heap
let minHeap = new PriorityQueue();
minHeap.enqueue(4);
minHeap.enqueue(6);
minHeap.enqueue(8);
minHeap.enqueue(9);
minHeap.enqueue(10);
let element = 6; // Element to search for
let found = false;
// Copy the min heap to a temporary queue and search for the element
let temp = new PriorityQueue(minHeap);
while (temp.size() > 0) {
if (temp.peek() == element) {
found = true;
break;
}
temp.dequeue();
}
if (found) {
console.log("Element found in the min heap.");
} else {
console.log("Element not found in the min heap.");
}
OutputElement found in the min heap.
Complexity Analysis
The time complexity of this program is O(n log n), where n is the number of elements in the priority queue.
The insertion operation has a time complexity of O(log n) in the worst case because the heap property needs to be maintained. The search operation involves copying the priority queue to a temporary queue and then traversing the temporary queue, which takes O(n log n) time in the worst case because each element needs to be copied and popped from the queue, and the priority queue needs to be rebuilt for each operation.
The space complexity of the program is O(n) because it stores n elements in the priority queue and creates a temporary queue with n elements.
Applications of Min-Heap Data Structure
- Heap sort: Min heap is used as a key component in heap sort algorithm which is an efficient sorting algorithm with a time complexity of O(nlogn).
- Priority Queue: A priority queue can be implemented using a min heap data structure where the element with the minimum value is always at the root.
- Dijkstra’s algorithm: In Dijkstra’s algorithm, a min heap is used to store the vertices of the graph with the minimum distance from the starting vertex. The vertex with the minimum distance is always at the root of the heap.
- Huffman coding: In Huffman coding, a min heap is used to implement a priority queue to build an optimal prefix code for a given set of characters.
- Merge K sorted arrays: Given K sorted arrays, we can merge them into a single sorted array efficiently using a min heap data structure.
Advantages of Min-heap Data Structure
- Efficient insertion and deletion: Min heap allows fast insertion and deletion of elements with a time complexity of O(log n), where n is the number of elements in the heap.
- Efficient retrieval of minimum element: The minimum element in a min heap is always at the root of the heap, which can be retrieved in O(1) time.
- Space efficient: Min heap is a compact data structure that can be implemented using an array or a binary tree, which makes it space efficient.
- Sorting: Min heap can be used to implement an efficient sorting algorithm such as heap sort with a time complexity of O(n log n).
- Priority Queue: Min heap can be used to implement a priority queue, where the element with the minimum priority can be retrieved efficiently in O(1) time.
- Versatility: Min heap has several applications in computer science, including graph algorithms, data compression, and database systems.
Overall, min heap is a useful and versatile data structure that offers efficient operations, space efficiency, and has several applications in computer science.
Similar Reads
DSA Tutorial - Learn Data Structures and Algorithms DSA (Data Structures and Algorithms) is the study of organizing data efficiently using data structures like arrays, stacks, and trees, paired with step-by-step procedures (or algorithms) to solve problems effectively. Data structures manage how data is stored and accessed, while algorithms focus on
7 min read
Basics & Prerequisites
Data Structures
Getting Started with Array Data StructureArray is a collection of items of the same variable type that are stored at contiguous memory locations. It is one of the most popular and simple data structures used in programming. Basic terminologies of ArrayArray Index: In an array, elements are identified by their indexes. Array index starts fr
14 min read
String in Data StructureA string is a sequence of characters. The following facts make string an interesting data structure.Small set of elements. Unlike normal array, strings typically have smaller set of items. For example, lowercase English alphabet has only 26 characters. ASCII has only 256 characters.Strings are immut
2 min read
Hashing in Data StructureHashing is a technique used in data structures that efficiently stores and retrieves data in a way that allows for quick access. Hashing involves mapping data to a specific index in a hash table (an array of items) using a hash function. It enables fast retrieval of information based on its key. The
2 min read
Linked List Data StructureA linked list is a fundamental data structure in computer science. It mainly allows efficient insertion and deletion operations compared to arrays. Like arrays, it is also used to implement other data structures like stack, queue and deque. Here’s the comparison of Linked List vs Arrays Linked List:
2 min read
Stack Data StructureA Stack is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out). LIFO implies that the element that is inserted last, comes out first and FILO implies that the element that is inserted first
2 min read
Queue Data StructureA Queue Data Structure is a fundamental concept in computer science used for storing and managing data in a specific order. It follows the principle of "First in, First out" (FIFO), where the first element added to the queue is the first one to be removed. It is used as a buffer in computer systems
2 min read
Tree Data StructureTree Data Structure is a non-linear data structure in which a collection of elements known as nodes are connected to each other via edges such that there exists exactly one path between any two nodes. Types of TreeBinary Tree : Every node has at most two childrenTernary Tree : Every node has at most
4 min read
Graph Data StructureGraph Data Structure is a collection of nodes connected by edges. It's used to represent relationships between different entities. If you are looking for topic-wise list of problems on different topics like DFS, BFS, Topological Sort, Shortest Path, etc., please refer to Graph Algorithms. Basics of
3 min read
Trie Data StructureThe Trie data structure is a tree-like structure used for storing a dynamic set of strings. It allows for efficient retrieval and storage of keys, making it highly effective in handling large datasets. Trie supports operations such as insertion, search, deletion of keys, and prefix searches. In this
15+ min read
Algorithms
Searching AlgorithmsSearching algorithms are essential tools in computer science used to locate specific items within a collection of data. In this tutorial, we are mainly going to focus upon searching in an array. When we search an item in an array, there are two most common algorithms used based on the type of input
2 min read
Sorting AlgorithmsA Sorting Algorithm is used to rearrange a given array or list of elements in an order. For example, a given array [10, 20, 5, 2] becomes [2, 5, 10, 20] after sorting in increasing order and becomes [20, 10, 5, 2] after sorting in decreasing order. There exist different sorting algorithms for differ
3 min read
Introduction to RecursionThe process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. A recursive algorithm takes one step toward solution and then recursively call itself to further move. The algorithm stops once we reach the solution
14 min read
Greedy AlgorithmsGreedy algorithms are a class of algorithms that make locally optimal choices at each step with the hope of finding a global optimum solution. At every step of the algorithm, we make a choice that looks the best at the moment. To make the choice, we sometimes sort the array so that we can always get
3 min read
Graph AlgorithmsGraph is a non-linear data structure like tree data structure. The limitation of tree is, it can only represent hierarchical data. For situations where nodes or vertices are randomly connected with each other other, we use Graph. Example situations where we use graph data structure are, a social net
3 min read
Dynamic Programming or DPDynamic Programming is an algorithmic technique with the following properties.It is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of
3 min read
Bitwise AlgorithmsBitwise algorithms in Data Structures and Algorithms (DSA) involve manipulating individual bits of binary representations of numbers to perform operations efficiently. These algorithms utilize bitwise operators like AND, OR, XOR, NOT, Left Shift, and Right Shift.BasicsIntroduction to Bitwise Algorit
4 min read
Advanced
Segment TreeSegment Tree is a data structure that allows efficient querying and updating of intervals or segments of an array. It is particularly useful for problems involving range queries, such as finding the sum, minimum, maximum, or any other operation over a specific range of elements in an array. The tree
3 min read
Pattern SearchingPattern searching algorithms are essential tools in computer science and data processing. These algorithms are designed to efficiently find a particular pattern within a larger set of data. Patten SearchingImportant Pattern Searching Algorithms:Naive String Matching : A Simple Algorithm that works i
2 min read
GeometryGeometry is a branch of mathematics that studies the properties, measurements, and relationships of points, lines, angles, surfaces, and solids. From basic lines and angles to complex structures, it helps us understand the world around us.Geometry for Students and BeginnersThis section covers key br
2 min read
Interview Preparation
Practice Problem