Painting Fence Algorithm

Try it on GfG Practice

Given a fence with n posts and k colors, the task is to find out the number of ways of painting the fence so that not more than two consecutive posts have the same color.

Examples:

Input: n = 2, k = 4
Output: 16
Explanation: We have 4 colors and 2 posts.
Ways when both posts have same color: 4 
Ways when both posts have diff color: 4(choices for 1st post) * 3(choices for 2nd post) = 12

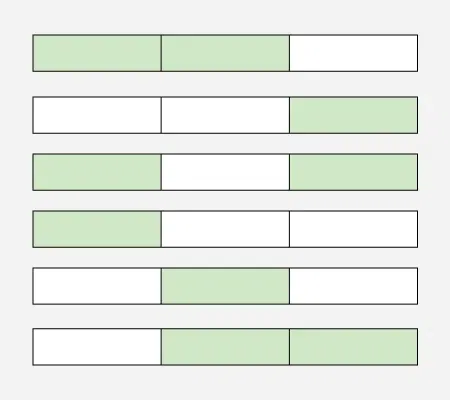
Input: n = 3, k = 2
Output: 6
Explanation: The following image depicts the 6 possible ways of painting 3 posts with 2 colors:

Using Recursion - O(2^n) Time and O(n) Space

The idea is to define our solution in terms of two choices: painting the last post a different color from the previous one or painting the last two posts the same color. This gives us the recurrence relation:

countWays(n) = countWays(n-1)*(k-1) + countWays(n-2)*(k-1)

Case 1: Different Color for the Last Post
If we paint the last post a different color from the one before it, we have k-1 choices (all colors except the previous post’s color). This means the number of ways to paint the first n-1 posts is multiplied by k-1.

Case 2: Same Color for the Last Two Posts
If the last two posts are the same color, they must differ from the post before them (the third-last post). Thus, we have k-1 choices for the last two posts, and the number of ways to paint the first n-2 posts is given by countWays(n-2).

Consider the following image, in which c, c' and c'' are the respective colors of posts i, i-1, and i-2.

// C++ program for Painting Fence Algorithm
// using recursion
#include <bits/stdc++.h>
using namespace std;

// Returns count of ways to color k posts
int countWays(int n, int k) {
    
    // base cases
    if (n == 1) return k;
    if (n == 2) return k*k;
    
    // Ways in which last fence 
    // is of different color.
    int cnt1 = countWays(n-1,k)*(k-1);
    
    // Ways in which last 2 fences
    // are of same color.
    int cnt2 = countWays(n-2,k)*(k-1);
    
    return cnt1 + cnt2;
}

int main() {
  
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

// Java program for Painting Fence Algorithm
// using recursion

class GfG {

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        // Ways in which last fence 
        // is of different color.
        int cnt1 = countWays(n - 1, k) * (k - 1);
        
        // Ways in which last 2 fences
        // are of same color.
        int cnt2 = countWays(n - 2, k) * (k - 1);
        
        return cnt1 + cnt2;
    }

    public static void main(String[] args) {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}

# Python program for Painting Fence Algorithm
# using recursion

# Returns count of ways to color k posts
def countWays(n, k):
    
    # base cases
    if n == 1:
        return k
    if n == 2:
        return k * k
    
    # Ways in which last fence 
    # is of different color.
    cnt1 = countWays(n - 1, k) * (k - 1)
    
    # Ways in which last 2 fences
    # are of same color.
    cnt2 = countWays(n - 2, k) * (k - 1)
    
    return cnt1 + cnt2

if __name__ == "__main__":
    n = 3
    k = 2
    print(countWays(n, k))

// C# program for Painting Fence
// using recursion

using System;

class GfG {

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        // Ways in which last fence 
        // is of different color.
        int cnt1 = countWays(n - 1, k) * (k - 1);
        
        // Ways in which last 2 fences
        // are of same color.
        int cnt2 = countWays(n - 2, k) * (k - 1);
        
        return cnt1 + cnt2;
    }

    static void Main(string[] args) {
        int n = 3, k = 2;
        Console.WriteLine(countWays(n, k));
    }
}

// JavaScript program for Painting
// Fence using recursion

// Returns count of ways to color k posts
function countWays(n, k) {
    
    // base cases
    if (n === 1) return k;
    if (n === 2) return k * k;
    
    // Ways in which last fence 
    // is of different color.
    let cnt1 = countWays(n - 1, k) * (k - 1);
    
    // Ways in which last 2 fences
    // are of same color.
    let cnt2 = countWays(n - 2, k) * (k - 1);
    
    return cnt1 + cnt2;
}

let n = 3, k = 2;
console.log(countWays(n, k));

6

Using Top-Down DP (Memoization) – O(n) Time and O(n) Space

If we notice carefully, we can observe that the above recursive solution holds the following two properties of Dynamic Programming:

1. Optimal Substructure:

Number of ways to paint the nth fence, i.e., countWays(n), depends on the solutions of the subproblems countWays(n-1) , and countWays(n-2). By adding these optimal substructures, we can efficiently calculate the total number of ways to reach the nth fence.

2. Overlapping Subproblems:

While applying a recursive approach in this problem, we notice that certain subproblems are computed multiple times. For example, when calculating countWays(4), we recursively calculate countWays(3) and countWays(2) which in turn will recursively compute countWays(2) again. This redundancy leads to overlapping subproblems.

• There is only one parameter that changes in the recursive solution and it can go from 1 to n. So we create a 1D array of size n+1 for memoization.
• We initialize this array as -1 to indicate nothing is computed initially.
• Now we modify our recursive solution to first check if the value is -1, then only make recursive calls. This way, we avoid re-computations of the same subproblems.

// C++ program for Painting Fence Algorithm
// using memoization
#include <bits/stdc++.h>
using namespace std;

int countWaysRecur(int n, int k, vector<int> &memo) {
    
    // base cases
    if (n == 1) return k;
    if (n == 2) return k*k;
    
    if (memo[n] != -1) return memo[n];
    
    // Ways in which last fence 
    // is of different color.
    int cnt1 = countWaysRecur(n-1, k, memo)*(k-1);
    
    // Ways in which last 2 fences
    // are of same color.
    int cnt2 = countWaysRecur(n-2, k, memo)*(k-1);
    
    return memo[n] = cnt1+cnt2;
}

// Returns count of ways to color k posts
int countWays(int n, int k) {
    
    vector<int> memo(n + 1, -1);
    return countWaysRecur(n, k, memo);
}

int main() {
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

// Java program for Painting Fence Algorithm
// using memoization
import java.util.Arrays;

class GfG {

    static int countWaysRecur(int n, int k, int[] memo) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        if (memo[n] != -1) return memo[n];
        
        // Ways in which last fence 
        // is of different color.
        int cnt1 = countWaysRecur(n - 1, k, memo) * (k - 1);
        
        // Ways in which last 2 fences
        // are of same color.
        int cnt2 = countWaysRecur(n - 2, k, memo) * (k - 1);
        
        return memo[n] = cnt1 + cnt2;
    }

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        int[] memo = new int[n + 1];
        Arrays.fill(memo, -1);
        return countWaysRecur(n, k, memo);
    }

    public static void main(String[] args) {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}

# Python program for Painting Fence Algorithm
# using memoization

def countWaysRecur(n, k, memo):
    
    # base cases
    if n == 1:
        return k
    if n == 2:
        return k * k
    
    if memo[n] != -1:
        return memo[n]
    
    # Ways in which last fence 
    # is of different color.
    cnt1 = countWaysRecur(n - 1, k, memo) * (k - 1)
    
    # Ways in which last 2 fences
    # are of same color.
    cnt2 = countWaysRecur(n - 2, k, memo) * (k - 1)
    
    memo[n] = cnt1 + cnt2
    return memo[n]

# Returns count of ways to color k posts
def countWays(n, k):
    
    memo = [-1] * (n + 1)
    return countWaysRecur(n, k, memo)

if __name__ == "__main__":
    n = 3
    k = 2
    print(countWays(n, k))

// C# program for Painting Fence Algorithm
// using memoization

using System;

class GfG {

    static int countWaysRecur(int n, int k, int[] memo) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        if (memo[n] != -1) return memo[n];
        
        // Ways in which last fence 
        // is of different color.
        int cnt1 = countWaysRecur(n - 1, k, memo) * (k - 1);
        
        // Ways in which last 2 fences
        // are of same color.
        int cnt2 = countWaysRecur(n - 2, k, memo) * (k - 1);
        
        return memo[n] = cnt1 + cnt2;
    }

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        int[] memo = new int[n + 1];
        Array.Fill(memo, -1);
        return countWaysRecur(n, k, memo);
    }

    static void Main(string[] args) {
        int n = 3, k = 2;
        Console.WriteLine(countWays(n, k));
    }
}

// JavaScript program for Painting Fence Algorithm
// using memoization

function countWaysRecur(n, k, memo) {
    
    // base cases
    if (n === 1) return k;
    if (n === 2) return k * k;
    
    if (memo[n] !== -1) return memo[n];
    
    // Ways in which last fence 
    // is of different color.
    let cnt1 = countWaysRecur(n - 1, k, memo) * (k - 1);
    
    // Ways in which last 2 fences
    // are of same color.
    let cnt2 = countWaysRecur(n - 2, k, memo) * (k - 1);
    
    memo[n] = cnt1 + cnt2;
    return memo[n];
}

// Returns count of ways to color k posts
function countWays(n, k) {
    
    let memo = new Array(n + 1).fill(-1);
    return countWaysRecur(n, k, memo);
}

let n = 3, k = 2;
console.log(countWays(n, k));

6

Using Bottom-Up DP (Tabulation) – O(n) Time and O(n) Space

The idea is to create a 1-D array, fill values for first two fences and compute the values from 3 to n using the previous two results. For i = 3 to n, do dp[i] = dp[i-1]*(k-1) + dp[i-2]*(k-1).

// C++ program for Painting Fence Algorithm
// using tabulation
#include <bits/stdc++.h>
using namespace std;

// Returns count of ways to color k posts
int countWays(int n, int k) {
    
    // base cases
    if (n == 1) return k;
    if (n == 2) return k*k;
    
    vector<int> dp(n+1);
    
    // Fill value for 1 and 2 fences
    dp[1] = k;
    dp[2] = k*k;
    
    for (int i=3; i<=n; i++) {
        dp[i] = dp[i-1]*(k-1) + dp[i-2]*(k-1);
    }
    
    return dp[n];
}

int main() {
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

// Java program for Painting Fence Algorithm
// using tabulation

import java.util.Arrays;

class GfG {

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        int[] dp = new int[n + 1];
        
        // Fill value for 1 and 2 fences
        dp[1] = k;
        dp[2] = k * k;
        
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] * (k - 1) + dp[i - 2] * (k - 1);
        }
        
        return dp[n];
    }

    public static void main(String[] args) {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}

# Python program for Painting Fence Algorithm
# using tabulation

def countWays(n, k):
    
    # base cases
    if n == 1:
        return k
    if n == 2:
        return k * k
    
    dp = [0] * (n + 1)
    
    # Fill value for 1 and 2 fences
    dp[1] = k
    dp[2] = k * k
    
    for i in range(3, n + 1):
        dp[i] = dp[i - 1] * (k - 1) + dp[i - 2] * (k - 1)
    
    return dp[n]

if __name__ == "__main__":
    n = 3
    k = 2
    print(countWays(n, k))

// C# program for Painting Fence Algorithm
// using tabulation
using System;

class GfG {

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        int[] dp = new int[n + 1];
        
        // Fill value for 1 and 2 fences
        dp[1] = k;
        dp[2] = k * k;
        
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] * (k - 1) + dp[i - 2] * (k - 1);
        }
        
        return dp[n];
    }

    static void Main(string[] args) {
        int n = 3, k = 2;
        Console.WriteLine(countWays(n, k));
    }
}

// JavaScript program for Painting Fence Algorithm
// using tabulation

function countWays(n, k) {
    
    // base cases
    if (n === 1) return k;
    if (n === 2) return k * k;
    
    let dp = new Array(n + 1).fill(0);
    
    // Fill value for 1 and 2 fences
    dp[1] = k;
    dp[2] = k * k;
    
    for (let i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] * (k - 1) + dp[i - 2] * (k - 1);
    }
    
    return dp[n];
}

let n = 3, k = 2;
console.log(countWays(n, k));

6

Using Space Optimized DP – O(n) Time and O(1) Space

The idea is to store only the previous two computed values. We can observe that for a given fence, only the result of last three fences are needed. So only store these three values and update them after each step.

// C++ program for Painting Fence Algorithm
// using space optimised

#include <bits/stdc++.h>
using namespace std;

// Returns count of ways to color k posts
int countWays(int n, int k) {
    
    // base cases
    if (n == 1) return k;
    if (n == 2) return k*k;
    
    // Fill value for 1 and 2 fences
    int prev2 = k;
    int prev1 = k*k;
    
    for (int i = 3; i <= n; i++) {
        int curr = prev1*(k-1) + prev2*(k-1);
        
        // update the values
        prev2 = prev1;
        prev1 = curr;
    }
    
    return prev1;
}

int main() {
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

// Java program for Painting Fence Algorithm
// using space optimised

class GfG {

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        // Fill value for 1 and 2 fences
        int prev2 = k;
        int prev1 = k * k;
        
        for (int i = 3; i <= n; i++) {
            int curr = prev1 * (k - 1) + prev2 * (k - 1);
            
            // update the values
            prev2 = prev1;
            prev1 = curr;
        }
        
        return prev1;
    }

    public static void main(String[] args) {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}

# Python program for Painting Fence Algorithm
# using space optimised

def countWays(n, k):
    
    # base cases
    if n == 1:
        return k
    if n == 2:
        return k * k
    
    # Fill value for 1 and 2 fences
    prev2 = k
    prev1 = k * k
    
    for i in range(3, n + 1):
        curr = prev1 * (k - 1) + prev2 * (k - 1)
        
        # update the values
        prev2 = prev1
        prev1 = curr
    
    return prev1

if __name__ == "__main__":
    n = 3
    k = 2
    print(countWays(n, k))

// C# program for Painting Fence Algorithm
// using space optimised

using System;

class GfG {

    // Returns count of ways to color k posts
    static int countWays(int n, int k) {
        
        // base cases
        if (n == 1) return k;
        if (n == 2) return k * k;
        
        // Fill value for 1 and 2 fences
        int prev2 = k;
        int prev1 = k * k;
        
        for (int i = 3; i <= n; i++) {
            int curr = prev1 * (k - 1) + prev2 * (k - 1);
            
            // update the values
            prev2 = prev1;
            prev1 = curr;
        }
        
        return prev1;
    }

    static void Main(string[] args) {
        int n = 3, k = 2;
        Console.WriteLine(countWays(n, k));
    }
}

// JavaScript program for Painting Fence Algorithm
// using space optimised

function countWays(n, k) {
    
    // base cases
    if (n === 1) return k;
    if (n === 2) return k * k;
    
    // Fill value for 1 and 2 fences
    let prev2 = k;
    let prev1 = k * k;
    
    for (let i = 3; i <= n; i++) {
        let curr = prev1 * (k - 1) + prev2 * (k - 1);
        
        // update the values
        prev2 = prev1;
        prev1 = curr;
    }
    
    return prev1;
}

let n = 3, k = 2;
console.log(countWays(n, k));

6