Given n items where each item has some weight and profit associated with it and also given a bag with capacity W, [i.e., the bag can hold at most W weight in it]. The task is to put the items into the bag such that the sum of profits associated with them is the maximum possible.
Note: The constraint here is we can either put an item completely into the bag or cannot put it at all [It is not possible to put a part of an item into the bag].
Input: W = 4, profit[] = [1, 2, 3], weight[] = [4, 5, 1]
Output: 3
Explanation: There are two items which have weight less than or equal to 4. If we select the item with weight 4, the possible profit is 1. And if we select the item with weight 1, the possible profit is 3. So the maximum possible profit is 3. Note that we cannot put both the items with weight 4 and 1 together as the capacity of the bag is 4.
Input: W = 3, profit[] = [1, 2, 3], weight[] = [4, 5, 6]
Output: 0
[Naive Approach] Using Recursion O(2^n) Time and O(n) Space
A simple solution is to consider all subsets of items and calculate the total weight and value of all subsets. Consider the only subsets whose total weight is smaller than W. From all such subsets, pick the subset with maximum value.
Optimal Substructure: To consider all subsets of items, there can be two cases for every item.
- Case 1: The item is included in the optimal subset.
- Case 2: The item is not included in the optimal set.
Follow the below steps to solve the problem:
The maximum value obtained from ‘n’ items is the max of the following two values.
- Case 1 (pick the nth item): Value of the nth item + maximum value obtained by remaining (n-1) items and remaining weight i.e. (W-weight of the nth item).
- Case 2 (don’t pick the nth item): Maximum value obtained by (n-1) items and W weight.
- If the weight of the ‘nth‘ item is greater than ‘W’, then the nth item cannot be included and Case 2 is the only possibility.
C++
#include <bits/stdc++.h>
using namespace std;
// Returns the maximum value that
// can be put in a knapsack of capacity W
int knapsackRec(int W, vector<int> &val, vector<int> &wt, int n) {
// Base Case
if (n == 0 || W == 0)
return 0;
int pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1);
// Don't pick the nth item
int notPick = knapsackRec(W, val, wt, n - 1);
return max(pick, notPick);
}
int knapsack(int W, vector<int> &val, vector<int> &wt) {
int n = val.size();
return knapsackRec(W, val, wt, n);
}
int main() {
vector<int> val = {1, 2, 3};
vector<int> wt = {4, 5, 1};
int W = 4;
cout << knapsack(W, val, wt) << endl;
return 0;
}
import java.util.*;
class GfG {
// Returns the maximum value that
// can be put in a knapsack of capacity W
static int knapsackRec(int W, int[] val, int[] wt, int n) {
// Base Case
if (n == 0 || W == 0)
return 0;
int pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1);
// Don't pick the nth item
int notPick = knapsackRec(W, val, wt, n - 1);
return Math.max(pick, notPick);
}
static int knapsack(int W, int[] val, int[] wt) {
int n = val.length;
return knapsackRec(W, val, wt, n);
}
public static void main(String[] args) {
int[] val = {1, 2, 3};
int[] wt = {4, 5, 1};
int W = 4;
System.out.println(knapsack(W, val, wt));
}
}
# Returns the maximum value that
# can be put in a knapsack of capacity W
def knapsackRec(W, val, wt, n):
# Base Case
if n == 0 or W == 0:
return 0
pick = 0
# Pick nth item if it does not exceed the capacity of knapsack
if wt[n - 1] <= W:
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1)
# Don't pick the nth item
notPick = knapsackRec(W, val, wt, n - 1)
return max(pick, notPick)
def knapsack(W, val, wt):
n = len(val)
return knapsackRec(W, val, wt, n)
if __name__ == "__main__":
val = [1, 2, 3]
wt = [4, 5, 1]
W = 4
print(knapsack(W, val, wt))
using System;
class GfG {
// Returns the maximum value that
// can be put in a knapsack of capacity W
static int knapsackRec(int W, int[] val, int[] wt, int n) {
// Base Case
if (n == 0 || W == 0)
return 0;
int pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1);
// Don't pick the nth item
int notPick = knapsackRec(W, val, wt, n - 1);
return Math.Max(pick, notPick);
}
static int knapsack(int W, int[] val, int[] wt) {
int n = val.Length;
return knapsackRec(W, val, wt, n);
}
static void Main() {
int[] val = { 1, 2, 3 };
int[] wt = { 4, 5, 1 };
int W = 4;
Console.WriteLine(knapsack(W, val, wt));
}
}
// Returns the maximum value that
// can be put in a knapsack of capacity W
function knapsackRec(W, val, wt, n) {
// Base Case
if (n === 0 || W === 0)
return 0;
let pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1);
// Don't pick the nth item
let notPick = knapsackRec(W, val, wt, n - 1);
return Math.max(pick, notPick);
}
function knapsack(W, val, wt) {
let n = val.length;
return knapsackRec(W, val, wt, n);
}
// Driver Code
let val = [1, 2, 3];
let wt = [4, 5, 1];
let W = 4;
console.log(knapsack(W, val, wt));
Below is an example run of the above implementation.

[Better Approach 1] Using Top-Down DP (Memoization)- O(n x W) Time and Space
Note: The above function using recursion computes the same subproblems again and again. See the following recursion tree, K(1, 1) is being evaluated twice.
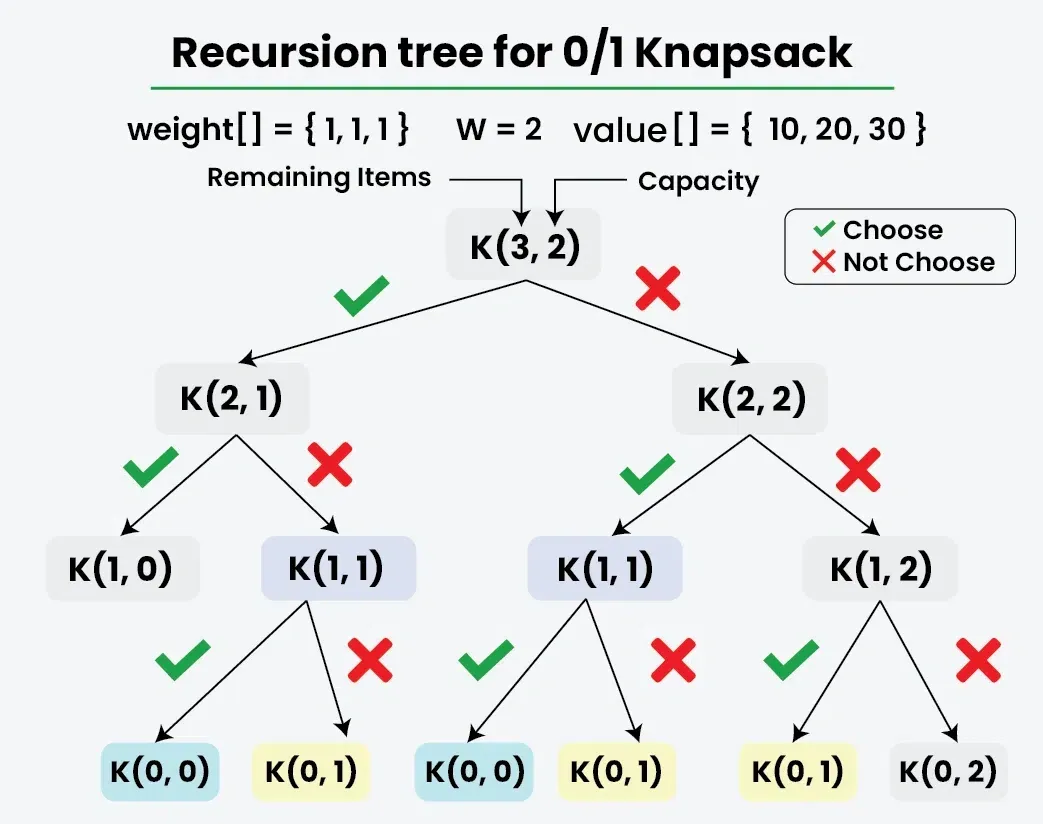
As there are repetitions of the same subproblem again and again we can implement the following idea to solve the problem.
If we get a subproblem the first time, we can solve this problem by creating a 2-D array that can store a particular state (n, w). Now if we come across the same state (n, w) again instead of calculating it i again we can directly return its result stored in the table in constant time.
C++
#include <bits/stdc++.h>
using namespace std;
// Returns the maximum value that
// can be put in a knapsack of capacity W
int knapsackRec(int W, vector<int> &val, vector<int> &wt, int n,
vector<vector<int>> &memo) {
// Base Case
if (n == 0 || W == 0)
return 0;
// Check if we have previously calculated the same subproblem
if(memo[n][W] != -1)
return memo[n][W];
int pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1, memo);
// Don't pick the nth item
int notPick = knapsackRec(W, val, wt, n - 1, memo);
// Store the result in memo[n][W] and return it
return memo[n][W] = max(pick, notPick);
}
int knapsack(int W, vector<int> &val, vector<int> &wt) {
int n = val.size();
// Memoization table to store the results
vector<vector<int>> memo(n + 1, vector<int>(W + 1, -1));
return knapsackRec(W, val, wt, n, memo);
}
int main() {
vector<int> val = {1, 2, 3};
vector<int> wt = {4, 5, 1};
int W = 4;
cout << knapsack(W, val, wt) << endl;
return 0;
}
import java.util.*;
class GfG {
// Returns the maximum value that
// can be put in a knapsack of capacity W
static int knapsackRec(int W, int[] val, int[] wt, int n, int[][] memo) {
// Base Case
if (n == 0 || W == 0)
return 0;
// Check if we have previously calculated the same subproblem
if (memo[n][W] != -1)
return memo[n][W];
int pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1, memo);
// Don't pick the nth item
int notPick = knapsackRec(W, val, wt, n - 1, memo);
// Store the result in memo[n][W] and return it
return memo[n][W] = Math.max(pick, notPick);
}
static int knapsack(int W, int[] val, int[] wt) {
int n = val.length;
// Memoization table to store the results
int[][] memo = new int[n + 1][W + 1];
// Initialize memoization table with -1
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= W; j++)
memo[i][j] = -1;
}
return knapsackRec(W, val, wt, n, memo);
}
public static void main(String[] args) {
int[] val = { 1, 2, 3 };
int[] wt = { 4, 5, 1 };
int W = 4;
System.out.println(knapsack(W, val, wt));
}
}
# Returns the maximum value that
# can be put in a knapsack of capacity W
def knapsackRec(W, val, wt, n, memo):
# Base Case
if n == 0 or W == 0:
return 0
# Check if we have previously calculated the same subproblem
if memo[n][W] != -1:
return memo[n][W]
pick = 0
# Pick nth item if it does not exceed the capacity of knapsack
if wt[n - 1] <= W:
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1, memo)
# Don't pick the nth item
notPick = knapsackRec(W, val, wt, n - 1, memo)
# Store the result in memo[n][W] and return it
memo[n][W] = max(pick, notPick)
return memo[n][W]
def knapsack(W, val, wt):
n = len(val)
# Memoization table to store the results
memo = [[-1] * (W + 1) for _ in range(n + 1)]
return knapsackRec(W, val, wt, n, memo)
if __name__ == "__main__":
val = [1, 2, 3]
wt = [4, 5, 1]
W = 4
print(knapsack(W, val, wt))
using System;
class GfG {
// Returns the maximum value that
// can be put in a knapsack of capacity W
static int KnapsackRec(int W, int[] val, int[] wt, int n, ref int[,] memo) {
// Base Case
if (n == 0 || W == 0)
return 0;
// Check if we have previously calculated the same subproblem
if (memo[n, W] != -1)
return memo[n, W];
int pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + KnapsackRec(W - wt[n - 1], val, wt, n - 1, ref memo);
// Don't pick the nth item
int notPick = KnapsackRec(W, val, wt, n - 1, ref memo);
// Store the result in memo[n, W] and return it
return memo[n, W] = Math.Max(pick, notPick);
}
static int Knapsack(int W, int[] val, int[] wt) {
int n = val.Length;
// Memoization table to store the results
int[,] memo = new int[n + 1, W + 1];
// Initialize memo table with -1
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= W; j++)
{
memo[i, j] = -1;
}
}
return KnapsackRec(W, val, wt, n, ref memo);
}
static void Main() {
int[] val = { 1, 2, 3 };
int[] wt = { 4, 5, 1 };
int W = 4;
Console.WriteLine(Knapsack(W, val, wt));
}
}
// Returns the maximum value that
// can be put in a knapsack of capacity W
function knapsackRec(W, val, wt, n, memo) {
// Base Case
if (n === 0 || W === 0)
return 0;
// Check if we have previously calculated the same subproblem
if (memo[n][W] !== -1)
return memo[n][W];
let pick = 0;
// Pick nth item if it does not exceed the capacity of knapsack
if (wt[n - 1] <= W)
pick = val[n - 1] + knapsackRec(W - wt[n - 1], val, wt, n - 1, memo);
// Don't pick the nth item
let notPick = knapsackRec(W, val, wt, n - 1, memo);
// Store the result in memo[n][W] and return it
memo[n][W] = Math.max(pick, notPick);
return memo[n][W];
}
function knapsack(W, val, wt) {
const n = val.length;
// Memoization table to store the results
const memo = Array.from({ length: n + 1 }, () => Array(W + 1).fill(-1));
return knapsackRec(W, val, wt, n, memo);
}
// Driver Code
const val = [1, 2, 3];
const wt = [4, 5, 1];
const W = 4;
console.log(knapsack(W, val, wt));
[Better Approach 2] Using Bottom-Up DP (Tabulation) – O(n x W) Time and Space
There are two parameters that change in the recursive solution and these parameters go from 0 to n and 0 to W. So we create a 2D dp[][] array of size (n+1) x (W+1), such that dp[i][j] stores the maximum value we can get using i items such that the knapsack capacity is j.
- We first fill the known entries when m is 0 or n is 0.
- Then we fill the remaining entries using the recursive formula.
For each item i and knapsack capacity j, we decide whether to pick the item or not.
- If we don’t pick the item: dp[i][j] remains same as the previous item, that is dp[i – 1][j].
- If we pick the item: dp[i][j] is updated to val[i] + dp[i – 1][j – wt[i]].
C++
#include <bits/stdc++.h>
using namespace std;
// Returns the maximum value that
// can be put in a knapsack of capacity W
int knapsack(int W, vector<int> &val, vector<int> &wt) {
int n = wt.size();
vector<vector<int>> dp(n + 1, vector<int>(W + 1));
// Build table dp[][] in bottom-up manner
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= W; j++) {
// If there is no item or the knapsack's capacity is 0
if (i == 0 || j == 0)
dp[i][j] = 0;
else {
int pick = 0;
// Pick ith item if it does not exceed the capacity of knapsack
if(wt[i - 1] <= j)
pick = val[i - 1] + dp[i - 1][j - wt[i - 1]];
// Don't pick the ith item
int notPick = dp[i - 1][j];
dp[i][j] = max(pick, notPick);
}
}
}
return dp[n][W];
}
int main() {
vector<int> val = {1, 2, 3};
vector<int> wt = {4, 5, 1};
int W = 4;
cout << knapsack(W, val, wt) << endl;
return 0;
}
import java.util.*;
class GfG {
// Returns the maximum value that
// can be put in a knapsack of capacity W
static int knapsack(int W, int[] val, int[] wt) {
int n = wt.length;
int[][] dp = new int[n + 1][W + 1];
// Build table dp[][] in bottom-up manner
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= W; j++) {
// If there is no item or the knapsack's capacity is 0
if (i == 0 || j == 0)
dp[i][j] = 0;
else {
int pick = 0;
// Pick ith item if it does not exceed the capacity of knapsack
if (wt[i - 1] <= j)
pick = val[i - 1] + dp[i - 1][j - wt[i - 1]];
// Don't pick the ith item
int notPick = dp[i - 1][j];
dp[i][j] = Math.max(pick, notPick);
}
}
}
return dp[n][W];
}
public static void main(String[] args) {
int[] val = {1, 2, 3};
int[] wt = {4, 5, 1};
int W = 4;
System.out.println(knapsack(W, val, wt));
}
}
def knapsack(W, val, wt):
n = len(wt)
dp = [[0 for _ in range(W + 1)] for _ in range(n + 1)]
# Build table dp[][] in bottom-up manner
for i in range(n + 1):
for j in range(W + 1):
# If there is no item or the knapsack's capacity is 0
if i == 0 or j == 0:
dp[i][j] = 0
else:
pick = 0
# Pick ith item if it does not exceed the capacity of knapsack
if wt[i - 1] <= j:
pick = val[i - 1] + dp[i - 1][j - wt[i - 1]]
# Don't pick the ith item
notPick = dp[i - 1][j]
dp[i][j] = max(pick, notPick)
return dp[n][W]
if __name__ == "__main__":
val = [1, 2, 3]
wt = [4, 5, 1]
W = 4
print(knapsack(W, val, wt))
using System;
using System.Linq;
class GfG {
// Returns the maximum value that
// can be put in a knapsack of capacity W
static int Knapsack(int W, int[] val, int[] wt) {
int n = wt.Length;
int[,] dp = new int[n + 1, W + 1];
// Build table dp[][] in bottom-up manner
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= W; j++) {
// If there is no item or the knapsack's capacity is 0
if (i == 0 || j == 0)
dp[i, j] = 0;
else {
int pick = 0;
// Pick ith item if it does not exceed the capacity of knapsack
if (wt[i - 1] <= j)
pick = val[i - 1] + dp[i - 1, j - wt[i - 1]];
// Don't pick the ith item
int notPick = dp[i - 1, j];
dp[i, j] = Math.Max(pick, notPick);
}
}
}
return dp[n, W];
}
static void Main() {
int[] val = { 1, 2, 3 };
int[] wt = { 4, 5, 1 };
int W = 4;
Console.WriteLine(Knapsack(W, val, wt));
}
}
// Returns the maximum value that
// can be put in a knapsack of capacity W
function knapsack(W, val, wt) {
let n = wt.length;
let dp = Array.from({ length: n + 1 }, () => Array(W + 1).fill(0));
// Build table dp[][] in bottom-up manner
for (let i = 0; i <= n; i++) {
for (let j = 0; j <= W; j++) {
// If there is no item or the knapsack's capacity is 0
if (i === 0 || j === 0)
dp[i][j] = 0;
else {
let pick = 0;
// Pick ith item if it does not exceed the capacity of knapsack
if (wt[i - 1] <= j)
pick = val[i - 1] + dp[i - 1][j - wt[i - 1]];
// Don't pick the ith item
let notPick = dp[i - 1][j];
dp[i][j] = Math.max(pick, notPick);
}
}
}
return dp[n][W];
}
// Driver code
let val = [1, 2, 3];
let wt = [4, 5, 1];
let W = 4;
console.log(knapsack(W, val, wt));
[Expected Approach] Using Bottom-Up DP (Space-Optimized) – O(n x W) Time and O(W) Space
For calculating the current row of the dp[] array we require only previous row, but if we start traversing the rows from right to left then it can be done with a single row only
C++
#include <bits/stdc++.h>
using namespace std;
// Function to find the maximum profit
int knapsack(int W, vector<int> &val, vector<int> &wt) {
// Initializing dp vector
vector<int> dp(W + 1, 0);
// Taking first i elements
for (int i = 1; i <= wt.size(); i++) {
// Starting from back, so that we also have data of
// previous computation of i-1 items
for (int j = W; j >= wt[i - 1]; j--) {
dp[j] = max(dp[j], dp[j - wt[i - 1]] + val[i - 1]);
}
}
return dp[W];
}
int main() {
vector<int> val = {1, 2, 3};
vector<int> wt = {4, 5, 1};
int W = 4;
cout << knapsack(W, val, wt) << endl;
return 0;
}
import java.util.*;
class GfG {
// Function to find the maximum profit
static int knapsack(int W, int[] val, int[] wt) {
// Initializing dp array
int[] dp = new int[W + 1];
// Taking first i elements
for (int i = 1; i <= wt.length; i++) {
// Starting from back, so that we also have data of
// previous computation of i-1 items
for (int j = W; j >= wt[i - 1]; j--) {
dp[j] = Math.max(dp[j], dp[j - wt[i - 1]] + val[i - 1]);
}
}
return dp[W];
}
public static void main(String[] args) {
int[] val = {1, 2, 3};
int[] wt = {4, 5, 1};
int W = 4;
System.out.println(knapsack(W, val, wt));
}
}
# Function to find the maximum profit
def knapsack(W, val, wt):
# Initializing dp list
dp = [0] * (W + 1)
# Taking first i elements
for i in range(1, len(wt) + 1):
# Starting from back, so that we also have data of
# previous computation of i-1 items
for j in range(W, wt[i - 1] - 1, -1):
dp[j] = max(dp[j], dp[j - wt[i - 1]] + val[i - 1])
return dp[W]
if __name__ == "__main__":
val = [1, 2, 3]
wt = [4, 5, 1]
W = 4
print(knapsack(W, val, wt))
using System;
class GfG {
// Function to find the maximum profit
static int Knapsack(int W, int[] val, int[] wt) {
// Initializing dp array
int[] dp = new int[W + 1];
// Taking first i elements
for (int i = 1; i <= wt.Length; i++) {
// Starting from back, so that we also have data of
// previous computation of i-1 items
for (int j = W; j >= wt[i - 1]; j--) {
dp[j] = Math.Max(dp[j], dp[j - wt[i - 1]] + val[i - 1]);
}
}
return dp[W];
}
static void Main() {
int[] val = { 1, 2, 3 };
int[] wt = { 4, 5, 1 };
int W = 4;
Console.WriteLine(Knapsack(W, val, wt));
}
}
// Function to find the maximum profit
function knapsack(W, val, wt) {
// Initializing dp array
let dp = new Array(W + 1).fill(0);
// Taking first i elements
for (let i = 1; i <= wt.length; i++) {
// Starting from back, so that we also have data of
// previous computation of i-1 items
for (let j = W; j >= wt[i - 1]; j--) {
dp[j] = Math.max(dp[j], dp[j - wt[i - 1]] + val[i - 1]);
}
}
return dp[W];
}
// Driver Code
let val = [1, 2, 3];
let wt = [4, 5, 1];
let W = 4;
console.log(knapsack(W, val, wt));
Problems based on 0-1 Knapsack
Similar Reads
Introduction to Knapsack Problem, its Types and How to solve them
The Knapsack problem is an example of the combinational optimization problem. This problem is also commonly known as the "Rucksack Problem". The name of the problem is defined from the maximization problem as mentioned below: Given a bag with maximum weight capacity of W and a set of items, each hav
6 min read
0/1 Knapsack
0/1 Knapsack Problem
Given n items where each item has some weight and profit associated with it and also given a bag with capacity W, [i.e., the bag can hold at most W weight in it]. The task is to put the items into the bag such that the sum of profits associated with them is the maximum possible. Note: The constraint
15+ min read
Printing Items in 0/1 Knapsack
Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays, val[0..n-1] and wt[0..n-1] represent values and weights associated with n items respectively. Also given an integer W which repre
12 min read
0/1 Knapsack Problem to print all possible solutions
Given weights and profits of N items, put these items in a knapsack of capacity W. The task is to print all possible solutions to the problem in such a way that there are no remaining items left whose weight is less than the remaining capacity of the knapsack. Also, compute the maximum profit.Exampl
10 min read
0-1 knapsack queries
Given an integer array W[] consisting of weights of the items and some queries consisting of capacity C of knapsack, for each query find maximum weight we can put in the knapsack. Value of C doesn't exceed a certain integer C_MAX. Examples: Input: W[] = {3, 8, 9} q = {11, 10, 4} Output: 11 9 3 If C
12 min read
0/1 Knapsack using Branch and Bound
Given two arrays v[] and w[] that represent values and weights associated with n items respectively. Find out the maximum value subset(Maximum Profit) of v[] such that the sum of the weights of this subset is smaller than or equal to Knapsack capacity W. Note: The constraint here is we can either pu
15+ min read
0/1 Knapsack using Least Cost Branch and Bound
Given N items with weights W[0..n-1], values V[0..n-1] and a knapsack with capacity C, select the items such that:Â Â The sum of weights taken into the knapsack is less than or equal to C.The sum of values of the items in the knapsack is maximum among all the possible combinations.Examples:Â Â Input:
15+ min read
Unbounded Fractional Knapsack
Given the weights and values of n items, the task is to put these items in a knapsack of capacity W to get the maximum total value in the knapsack, we can repeatedly put the same item and we can also put a fraction of an item. Examples: Input: val[] = {14, 27, 44, 19}, wt[] = {6, 7, 9, 8}, W = 50 Ou
5 min read
Unbounded Knapsack (Repetition of items allowed)
Given a knapsack weight, say capacity and a set of n items with certain value vali and weight wti, The task is to fill the knapsack in such a way that we can get the maximum profit. This is different from the classical Knapsack problem, here we are allowed to use an unlimited number of instances of
15+ min read
Unbounded Knapsack (Repetition of items allowed) | Efficient Approach
Given an integer W, arrays val[] and wt[], where val[i] and wt[i] are the values and weights of the ith item, the task is to calculate the maximum value that can be obtained using weights not exceeding W. Note: Each weight can be included multiple times. Examples: Input: W = 4, val[] = {6, 18}, wt[]
8 min read
Double Knapsack | Dynamic Programming
Given an array arr[] containing the weight of 'n' distinct items, and two knapsacks that can withstand capactiy1 and capacity2 weights, the task is to find the sum of the largest subset of the array 'arr', that can be fit in the two knapsacks. It's not allowed to break any items in two, i.e. an item
15+ min read
Some Problems of Knapsack problem
Partition a Set into Two Subsets of Equal Sum
Given an array arr[], the task is to check if it can be partitioned into two parts such that the sum of elements in both parts is the same.Note: Each element is present in either the first subset or the second subset, but not in both. Examples: Input: arr[] = [1, 5, 11, 5]Output: true Explanation: T
15+ min read
Count of subsets with sum equal to target
Given an array arr[] of length n and an integer target, the task is to find the number of subsets with a sum equal to target. Examples: Input: arr[] = [1, 2, 3, 3], target = 6 Output: 3 Explanation: All the possible subsets are [1, 2, 3], [1, 2, 3] and [3, 3] Input: arr[] = [1, 1, 1, 1], target = 1
15+ min read
Length of longest subset consisting of A 0s and B 1s from an array of strings
Given an array arr[] consisting of binary strings, and two integers a and b, the task is to find the length of the longest subset consisting of at most a 0s and b 1s. Examples: Input: arr[] = ["1" ,"0" ,"0001" ,"10" ,"111001"], a = 5, b = 3Output: 4Explanation: One possible way is to select the subs
15+ min read
Breaking an Integer to get Maximum Product
Given a number n, the task is to break n in such a way that multiplication of its parts is maximized. Input : n = 10Output: 36Explanation: 10 = 4 + 3 + 3 and 4 * 3 * 3 = 36 is the maximum possible product. Input: n = 8Output: 18Explanation: 8 = 2 + 3 + 3 and 2 * 3 * 3 = 18 is the maximum possible pr
15+ min read
Coin Change - Minimum Coins to Make Sum
Given an array of coins[] of size n and a target value sum, where coins[i] represent the coins of different denominations. You have an infinite supply of each of the coins. The task is to find the minimum number of coins required to make the given value sum. If it is not possible to form the sum usi
15+ min read
Coin Change - Count Ways to Make Sum
Given an integer array of coins[] of size n representing different types of denominations and an integer sum, the task is to count all combinations of coins to make a given value sum. Note: Assume that you have an infinite supply of each type of coin. Examples: Input: sum = 4, coins[] = [1, 2, 3]Out
15+ min read
Maximum sum of values of N items in 0-1 Knapsack by reducing weight of at most K items in half
Given weights and values of N items and the capacity W of the knapsack. Also given that the weight of at most K items can be changed to half of its original weight. The task is to find the maximum sum of values of N items that can be obtained such that the sum of weights of items in knapsack does no
15+ min read