Graph Measurements

A graph is defined as a set of points known as 'Vertices' and a line joining these points is known as 'Edges'. It is a set consisting of where 'V' is the vertices and 'E' is edges. 

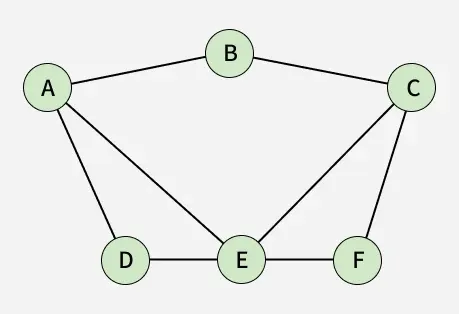
Vertices: {A, B, C, D, E, F} 
Edges: {{A, B}, {A, D}, {A, E}, {B, C}, {C, E}, {C, F}, {D, E}, {E, F}} 

Graph Measurements: There are a few graph measurement methods available: 

1. Length - 
The length of the graph is defined as the number of edges contained in the graph. 

Length of the graph: 8
AB, BC, CD, DE, EF, FA, AC, CE 

2. The distance between two Vertices - 
The distance between two vertices in a graph is the number of edges in a shortest or minimal path. It gives the available minimum distance between two edges. There can exist more than one shortest path between two vertices.  

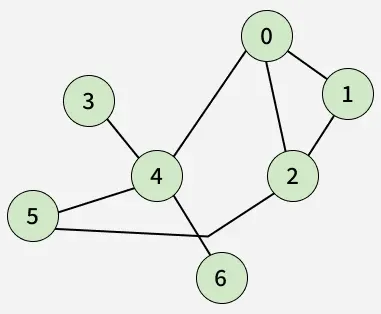
Shortest Distance between 1 - 5 is 2
1 → 2 → 5 

3. Eccentricity of graph - 
It is defined as the maximum distance of one vertex from another vertex. The maximum distance between a vertex to all other vertices is considered as the eccentricity of the vertex. It is denoted by e(V). 

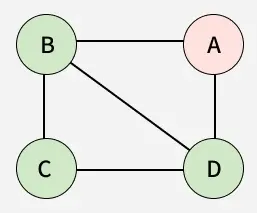
Eccentricity from:
(A, A) = 0
(A, B) = 1
(A, C) = 2
(A, D) = 1
Maximum value  is 2, So Eccentricity is 2

4. Diameter of graph - 
The diameter of a graph is the maximum distance between any pair of vertices. It can also be defined as the maximal distance between a pair of vertices. A way to solve it is to find all the paths and then find the maximum of all. It can also be found by finding the maximum value of eccentricity from all the vertices.

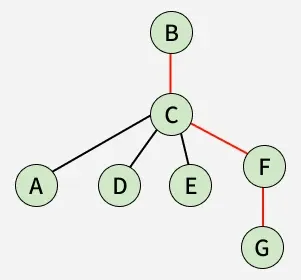
Diameter: 3
BC → CF → FG  
Here the eccentricity of the vertex B is 3 since (B,G) = 3. (Maximum Eccentricity of Graph)

5. Radius of graph -

A radius of the graph exists only if it has a diameter. The minimum among all the maximum distances between a vertex to all other vertices is considered as the radius of the Graph G. It is denoted as r(G). It can also be found by finding the minimum value of eccentricity from all the vertices.

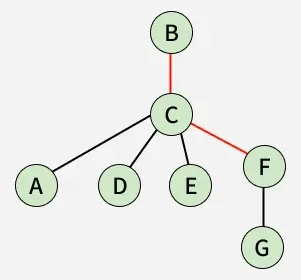
Radius: 2
All available minimum radius: 
BC → CF,
BC → CE,
BC → CD,
BC → CA

6. Centre of graph - 
It consists of all the vertices whose eccentricity is minimum. Here, the eccentricity is equal to the radius. For example, if the school is at the center of town, it will reduce the distance buses have to travel. If the eccentricity of two vertices is the same and minimum among all other both of them can be the center of the graph.

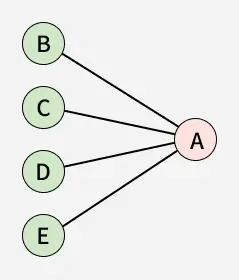
Centre: A  
Inorder to find the center of the graph, we need to find the eccentricity of each vertex and find the minimum among all of them. 
The minimum eccentricity vertex will be considered as the center.

Also Check

Understanding graph measurements is crucial for various algorithmic problems, especially in competitive exams like GATE. If you're preparing for GATE and want to dive deeper into graph theory concepts, the GATE CS Self-Paced Course offers comprehensive coverage on graph algorithms and measurements. This course is designed to simplify complex topics with clear explanations and practical examples, making graph theory easier to grasp.

Practices Problems

Question 1: Path Length Calculation:

• Given a simple undirected graph, find the length of the path between vertices A and D: A-B-C-D.
• Assume the graph has the following edges with equal weights of 1: A-B, B-C, and C-D.

Question 2: Shortest Path Distance:

In the following weighted graph, compute the shortest path distance between vertices A and E:

Question 3: Graph Diameter

For the graph below, determine its diameter. The diameter is the longest shortest path between any two vertices.

A -- B -- C -- D -- E

Question 4: Eccentricity Calculation

Find the eccentricity of vertex C in the graph below. The eccentricity of a vertex is the greatest distance from that vertex to any other vertex.

   A -- B -- C -- D -- E

Question 5: Graph Radius

Calculate the radius of the following graph. The radius is the minimum eccentricity of any vertex in the graph.

    A -- B -- C -- D -- E

Question 6: Graph Center

Identify the center of the given graph. The center consists of the vertices with eccentricity equal to the radius.

   A -- B -- C -- D -- E

Question 7: Weighted Graph Path Length

In a weighted graph, calculate the length of the path from vertex A to vertex F given the following edges with weights: A-B(2), B-C(3), C-D(1), D-E(4), and E-F(2).

Question 8: Maximal Distance Calculation

For the graph below, determine the maximum distance (longest shortest path) from vertex A to any other vertex.

Question 9: Determining Eccentricity in a Star Graph

For a star graph with a central vertex connected to 4 outer vertices, compute the eccentricity of the central vertex and one of the outer vertices.

Question 10: Graph Center and Radius for Complete Graph

For a complete graph ( K5 ) (5 vertices, each connected to every other vertex), determine the graph's radius and identify its center.

Related Articles

• Basic Properties of a Graph
• Graph Theory Tutorial
• Mathematics | Graph Theory Basics - Set 2
• Check whether a given graph is Bipartite or not