Given an unsorted array of integers, find a subarray that adds to a given number. If there is more than one subarray with the sum of the given number, print any of them.

Examples:  

Input: arr[] = {1, 4, 20, 3, 10, 5}, sum = 33
Output: Sum found between indexes 2 and 4
Explanation: Sum of elements between indices 2 and 4 is 20 + 3 + 10 = 33

Input: arr[] = {2, 12, -2, -20, 10}, sum = -10
Output: Sum found between indexes 1 to 3
Explanation: Sum of elements between indices 0 and 3 is 12 – 2 – 20 = -10

Input: arr[] = {-10, 0, 2, -2, -20, 10}, sum = 20
Output: No subarray with given sum exists
Explanation: There is no subarray with the given sum

Try it on GfG Practice

Note: We have discussed a solution that does not handle negative integers here. In this post, negative integers are also handled.

Naive Approach – O(n^2) Time and O(1) Space

A simple solution is to consider all subarrays one by one and check the sum of every subarray. The following program implements the simple solution. Run two loops: the outer loop picks a starting point I and the inner loop tries all subarrays starting from i.

Follow the given steps to solve the problem:

• Traverse the array from start to end.
• From every index start another loop from i to the end of the array to get all subarrays starting from i, and keep a variable sum to calculate the sum. For every index in the inner loop update sum = sum + array[j]If the sum is equal to the given sum then print the subarray.
• For every index in the inner loop update sum = sum + array[j]
• If the sum is equal to the given sum then print the subarray.

Below is the implementation of the above approach:

/* A simple program to print subarray
with sum as given sum */
#include <bits/stdc++.h>
using namespace std;

/* Returns true if the there is a subarray
of arr[] with sum equal to 'sum' otherwise
returns false. Also, prints the result */
int subArraySum(int arr[], int n, int sum)
{
    int curr_sum, i, j;

    // Pick a starting point
    for (i = 0; i < n; i++) {
        curr_sum = 0;

        // try all subarrays starting with 'i'
        for (j = i; j < n; j++) {
            curr_sum = curr_sum + arr[j];

            if (curr_sum == sum) {
                cout << "Sum found between indexes " << i
                     << " and " << j;
                return 1;
            }
        }
    }

    cout << "No subarray found";
    return 0;
}

// Driver Code
int main()
{
    int arr[] = { 15, 2, 4, 8, 9, 5, 10, 23 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int sum = 23;

    // Function call
    subArraySum(arr, n, sum);
    return 0;
}

// Java program for the above approach
import java.util.*;

class GFG {

    /* Returns true if the there is a subarray
    of arr[] with sum equal to 'sum' otherwise
    returns false. Also, prints the result */
    static int subArraySum(int arr[], int n, int sum)
    {
        int curr_sum, i, j;

        // Pick a starting point
        for (i = 0; i < n; i++) {
            curr_sum = 0;

            // try all subarrays starting with 'i'
            for (j = i; j < n; j++) {
                curr_sum = curr_sum + arr[j];

                if (curr_sum == sum) {
                    System.out.print(
                        "Sum found between indexes " + i
                        + " and " + j);
                    return 1;
                }
            }
        }

        System.out.print("No subarray found");
        return 0;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int arr[] = { 15, 2, 4, 8, 9, 5, 10, 23 };
        int n = arr.length;
        int sum = 23;

        // Function call
        subArraySum(arr, n, sum);
    }
}

// This code is contributed by code_hunt.

# Python3 program to print subarray
# with sum as given sum


# Returns true if the there is a subarray
# of arr[] with sum equal to 'sum' otherwise
# returns false. Also, prints the result */
def subArraySum(arr, n, sum):

    # Pick a starting point
    for i in range(n):
        curr_sum = 0
        # try all subarrays starting with 'i'
        for j in range(i, n):
            curr_sum += arr[j]
            if (curr_sum == sum):
                print("Sum found between indexes", i, "and", j)
                return

    print("No subarray found")


# Driver Code
if __name__ == "__main__":
    arr = [15, 2, 4, 8, 9, 5, 10, 23]
    n = len(arr)
    sum = 23

    # Function Call
    subArraySum(arr, n, sum)


# This code is contributed by phasing17

/* A simple program to print subarray
with sum as given sum */

using System;

public static class GFG {
    /* Returns true if the there is a subarray
    of arr[] with sum equal to 'sum' otherwise
    returns false. Also, prints the result */

    public static int subArraySum(int[] arr, int n, int sum)
    {
        int curr_sum;
        int i;
        int j;

        // Pick a starting point
        for (i = 0; i < n; i++) {
            curr_sum = 0;

            // try all subarrays starting with 'i'
            for (j = i; j < n; j++) {
                curr_sum = curr_sum + arr[j];

                if (curr_sum == sum) {
                    Console.Write(
                        "Sum found between indexes ");
                    Console.Write(i);
                    Console.Write(" and ");
                    Console.Write(j);
                    return 1;
                }
            }
        }

        Console.Write("No subarray found");
        return 0;
    }

    // Driver Code
    public static void Main()
    {
        int[] arr = { 15, 2, 4, 8, 9, 5, 10, 23 };
        int n = arr.Length;
        int sum = 23;

        // Function call
        subArraySum(arr, n, sum);
    }
}

// This code is contributed by Aarti_Rathi

/* JavaScript program to print subarray
with sum as given sum */

 
/* Returns true if the there is a subarray
of arr[] with sum equal to 'sum' otherwise
returns false. Also, prints the result */
function subArraySum(arr, n, sum)
{
    var curr_sum, i, j;
 
    // Pick a starting point
    for (i = 0; i < n; i++) {
        curr_sum = 0;
 
        // try all subarrays starting with 'i'
        for (j = i ; j < n; j++) {
           curr_sum = curr_sum + arr[j];
          
            if (curr_sum == sum) {
                console.log("Sum found between indexes " + i + " and " + j);
                return;
            }
        }
    }
 
    console.log("No subarray found");
}
 
// Driver Code
var arr = [ 15, 2, 4, 8, 9, 5, 10, 23 ];
var n = arr.length;
var sum = 23;

//Function Call
subArraySum(arr, n, sum);


//This code is contributed by phasing17

Sum found between indexes 1 and 4

Time Complexity: O(N²)
Auxiliary Space: O(1)

Expected Approach – Prefix Sum and Hash Map – O(n) time and O(n) Space

To solve the problem follow the below idea:

The idea is to store the sum of elements of every prefix of the array in a hashmap, i.e, every index stores the sum of elements up to that index hashmap. So to check if there is a subarray with a sum equal to target_sum, check for every index i, and sum up to that index as curr_sum. If there is a prefix with a sum equal to (curr_sum – target_sum), then the subarray with the given sum is found.

Follow the given steps to solve the problem:

• Create a Hashmap (hm) to store a key-value pair, i.e, key = prefix sum and value = its index, and a variable to store the current sum (curr_sum = 0).
• Traverse through the array from start to end.
• For every element update the curr_sum, i.e curr_sum = curr_sum + arr[i]
• If the sum is equal to target_sum then print that the subarray with the given sum is from 0 to i
• If there is any key in the HashMap which is equal to curr_sum – target_sum then print that the subarray with the given sum is from hm[curr_sum – target_sum] + 1 to i.
• Put the sum and index in the hashmap as a key-value pair.

Dry-run of the above approach: 

1 / 6

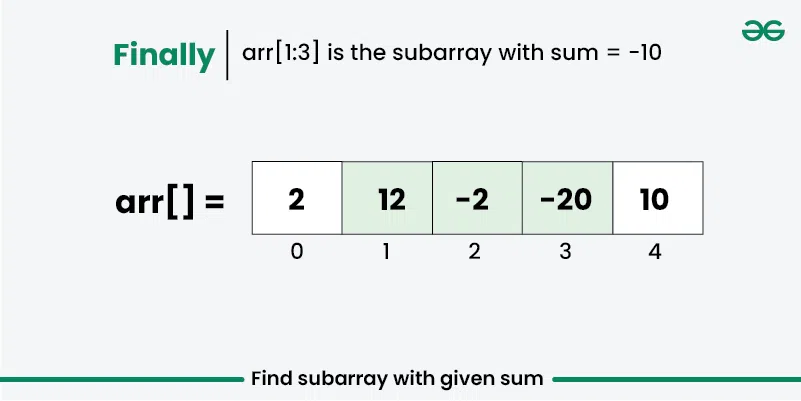
Below is the implementation of the above approach:

// C++ program to print subarray with sum as given sum
#include <bits/stdc++.h>
using namespace std;

// Function to print subarray with sum as given sum
void subArraySum(int arr[], int n, int sum)
{
    // create an empty map
    unordered_map<int, int> map;

    // Maintains sum of elements so far
    int curr_sum = 0;

    for (int i = 0; i < n; i++) {
        // add current element to curr_sum
        curr_sum = curr_sum + arr[i];

        // if curr_sum is equal to target sum
        // we found a subarray starting from index 0
        // and ending at index i
        if (curr_sum == sum) {
            cout << "Sum found between indexes " << 0
                 << " to " << i << endl;
            return;
        }

        // If curr_sum - sum already exists in map
        // we have found a subarray with target sum
        if (map.find(curr_sum - sum) != map.end()) {
            cout << "Sum found between indexes "
                 << map[curr_sum - sum] + 1 << " to " << i
                 << endl;
            return;
        }

        map[curr_sum] = i;
    }

    // If we reach here, then no subarray exists
    cout << "No subarray with given sum exists";
}

// Driver code
int main()
{
    int arr[] = { 2, 12, -2, -20, 10 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int sum = -10;

    // Function call
    subArraySum(arr, n, sum);

    return 0;
}

// Java program to print subarray with sum as given sum
import java.util.*;

class GFG {

    public static void subArraySum(int[] arr, int n,
                                   int sum)
    {
        // cur_sum to keep track of cumulative sum till that
        // point
        int cur_sum = 0;
        int start = 0;
        int end = -1;
        HashMap<Integer, Integer> hashMap = new HashMap<>();

        for (int i = 0; i < n; i++) {
            cur_sum = cur_sum + arr[i];
            // check whether cur_sum - sum = 0, if 0 it
            // means the sub array is starting from index 0-
            // so stop
            if (cur_sum - sum == 0) {
                start = 0;
                end = i;
                break;
            }
            // if hashMap already has the value, means we
            // already
            // have subarray with the sum - so stop
            if (hashMap.containsKey(cur_sum - sum)) {
                start = hashMap.get(cur_sum - sum) + 1;
                end = i;
                break;
            }
            // if value is not present then add to hashmap
            hashMap.put(cur_sum, i);
        }
        // if end is -1 : means we have reached end without
        // the sum
        if (end == -1) {
            System.out.println(
                "No subarray with given sum exists");
        }
        else {
            System.out.println("Sum found between indexes "
                               + start + " to " + end);
        }
    }

    // Driver code
    public static void main(String[] args)
    {
        int[] arr = { 2, 12, -2, -20, 10 };
        int n = arr.length;
        int sum = -10;

        // Function call
        subArraySum(arr, n, sum);
    }
}

# Python3 program to print subarray with sum as given sum

# Function to print subarray with sum as given sum
def subArraySum(arr, n, Sum):

    # create an empty map
    Map = {}

    # Maintains sum of elements so far
    curr_sum = 0

    for i in range(0, n):

        # add current element to curr_sum
        curr_sum = curr_sum + arr[i]

        # if curr_sum is equal to target sum
        # we found a subarray starting from index 0
        # and ending at index i
        if curr_sum == Sum:

            print("Sum found between indexes 0 to", i)
            return

        # If curr_sum - sum already exists in map
        # we have found a subarray with target sum
        if (curr_sum - Sum) in Map:

            print("Sum found between indexes",
                  Map[curr_sum - Sum] + 1, "to", i)

            return

        Map[curr_sum] = i

    # If we reach here, then no subarray exists
    print("No subarray with given sum exists")


# Driver code
if __name__ == "__main__":

    arr = [2, 12, -2, -20, 10]
    n = len(arr)
    Sum = -10

    # Function call
    subArraySum(arr, n, Sum)

using System;
using System.Collections.Generic;

// C# program to print subarray with sum as given sum

public class GFG {

    public static void subArraySum(int[] arr, int n,
                                   int sum)
    {
        // cur_sum to keep track of cumulative sum till that
        // point
        int cur_sum = 0;
        int start = 0;
        int end = -1;
        Dictionary<int, int> hashMap
            = new Dictionary<int, int>();

        for (int i = 0; i < n; i++) {
            cur_sum = cur_sum + arr[i];
            // check whether cur_sum - sum = 0, if 0 it
            // means the sub array is starting from index 0-
            // so stop
            if (cur_sum - sum == 0) {
                start = 0;
                end = i;
                break;
            }
            // if hashMap already has the value, means we
            // already
            // have subarray with the sum - so stop
            if (hashMap.ContainsKey(cur_sum - sum)) {
                start = hashMap[cur_sum - sum] + 1;
                end = i;
                break;
            }
            // if value is not present then add to hashmap
            hashMap[cur_sum] = i;
        }
        // if end is -1 : means we have reached end without
        // the sum
        if (end == -1) {
            Console.WriteLine(
                "No subarray with given sum exists");
        }
        else {
            Console.WriteLine("Sum found between indexes "
                              + start + " to " + end);
        }
    }

    // Driver code
    public static void Main(string[] args)
    {
        int[] arr = new int[] { 2, 12, -2, -20, 10 };
        int n = arr.Length;
        int sum = -10;

        // Function call
        subArraySum(arr, n, sum);
    }
}

// Javascript program to print subarray with sum as given sum

    function subArraySum(arr, n, sum) {
        //cur_sum to keep track of cumulative sum till that point
        let cur_sum = 0;
        let start = 0;
        let end = -1;
        let hashMap = new Map();
  
        for (let i = 0; i < n; i++) {
            cur_sum = cur_sum + arr[i];
            //check whether cur_sum - sum = 0, if 0 it means
            //the sub array is starting from index 0- so stop
            if (cur_sum - sum == 0) {
                start = 0;
                end = i;
                break;
            }
            //if hashMap already has the value, means we already 
            // have subarray with the sum - so stop
            if (hashMap.has(cur_sum - sum)) {
                start = hashMap.get(cur_sum - sum) + 1;
                end = i;
                break;
            }
            //if value is not present then add to hashmap
            hashMap.set(cur_sum, i);
  
        }
        // if end is -1 : means we have reached end without the sum
        if (end == -1) {
            console.log("No subarray with given sum exists");
        } 
        else {
            console.log("Sum found between indexes " 
                            + start + " to " + end);
        }
  
    }

// Driver program 

         let arr = [2, 12, -2, -20, 10];
        let n = arr.length;
        let sum = -10;
        subArraySum(arr, n, sum);

Sum found between indexes 1 to 3

Time complexity: O(N). If hashing is performed with the help of an array, then this is the time complexity. In case the elements cannot be hashed in an array a hash map can also be used as shown in the above code.
Auxiliary space: O(N). As a HashMap is needed, this takes linear space.