SARIMA (Seasonal Autoregressive Integrated Moving Average)
Last Updated :
22 Aug, 2025
SARIMA or Seasonal Autoregressive Integrated Moving Average is an extension of the traditional ARIMA model, specifically designed for time series data with seasonal patterns. While ARIMA is great for non-seasonal data, SARIMA introduces seasonal components to handle periodic fluctuations and provides better forecasting capabilities for seasonal data.
Understanding the Components of SARIMA
SARIMA consists of several components that help capture both short-term and long-term dependencies within a time series:
- Seasonal Component: Represents the repeating patterns or cycles in the data at regular intervals like yearly, monthly, daily, etc. This allows SARIMA to model seasonality effectively.
- Autoregressive (AR) Component: Models the relationship between current and past observations. It captures the autocorrelation of the data over time.
- Integrated (I) Component: Addresses non-stationarity by differencing the data to make it stationary which is crucial for time series analysis.
- Moving Average (MA) Component: Models the relationship between current observations and past residual errors. It helps in capturing short-term fluctuations.
SARIMA Notation
The SARIMA model is represented as:
SARIMA(p, d, q)(P, D, Q, s)
Parameters:
- p: Autoregressive order
- d: Number of non-seasonal differences
- q: Moving average order
- P: Seasonal autoregressive order
- D: Seasonal differencing order
- Q: Seasonal moving average order
- s: Length of the seasonal period (e.g., 12 for monthly data)
Before applying SARIMA, seasonal differencing is often required to make the data stationary. This process involves subtracting the current observation from one that corresponds to the same season in the previous cycle. Seasonal differencing helps remove the seasonal pattern from the data, enabling more accurate forecasting.
Understanding Mathematical Representation of SARIMA
The SARIMA model can be expressed mathematically as:
(1 - \phi_1 B) (1 - \Phi_1 B^s) (1 - B) (1 - B^s) y_t = (1 + \theta_1 B) (1 + \Theta_1 B^s) \epsilon_t
Parameters:
- y_t: The observed time series at time t
- B: The backshift operator (lag operator)
- \phi_1: Non-seasonal autoregressive coefficient
- \Phi_1: Seasonal autoregressive coefficient
- \theta_1: Non-seasonal moving average coefficient
- \Theta_1: Seasonal moving average coefficient
- s: Seasonal period
- \epsilon_t: The white noise error term
Implementing SARIMA in Time Series Forecasting
1. Importing Libraries
To begin working with SARIMA, we need to import the necessary libraries like Numpy, Pandas, Matplotlib, Statsmodels and Scikit-learn.
Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from sklearn.metrics import mean_absolute_error, mean_squared_error
2. Loading the Dataset
We will load a retail dataset to predict monthly sales for a global superstore.
- pd.read_csv(): Reads the CSV file into a DataFrame.
- df[['Order Date', 'Sales']]: Selects relevant columns ('Order Date' and 'Sales') for analysis.
- pd.to_datetime(): Converts 'Order Date' to datetime format for proper time series analysis.
Python
df = pd.read_csv("/content/Dataset- Superstore (2015-2018).csv")
sales_data = df[['Order Date', 'Sales']]
sales_data['Order Date'] = pd.to_datetime(sales_data['Order Date'])
sales_data.head()
Output:
 Dataset
DatasetWe will aggregate the data on a monthly basis to focus on trends rather than daily fluctuations.
- set_index('Order Date'): Sets 'Order Date' as the index of the DataFrame.
- resample('ME').sum(): Resamples the data to monthly frequency and calculates the total sum of sales for each month.
Python
df1 = sales_data.set_index('Order Date')
monthly_sales = df1.resample('ME').sum()
monthly_sales.head()
Output:
 Monthly Sales
Monthly Sales4. Plotting the Monthly Sales
Visualizing the sales data helps us identify seasonal patterns.
- plt.figure(figsize=(10, 6)): Sets the plot size.
- plt.plot(): Plots the data with specified line width and color.
- plt.title(), plt.xlabel(), plt.ylabel(): Adds title and labels to the plot.
- plt.show(): Displays the plot.
Python
plt.figure(figsize=(10, 6))
plt.plot(monthly_sales['Sales'], linewidth=3, c='deeppink')
plt.title("Monthly Sales")
plt.xlabel("Date")
plt.ylabel("Sales")
plt.show()
Output:
 Plotting Monthly Sales
Plotting Monthly Sales5. Stationarity Check
Before applying SARIMA, we need to check if the data is stationary. Stationary data has constant mean and variance, which is a key assumption for SARIMA. We use the Augmented Dickey-Fuller test (ADF) for this.
- adfuller(timeseries, autolag='AIC'): Performs the Augmented Dickey-Fuller test for stationarity.
- result[1]: Extracts the p-value from the ADF test to check for stationarity.
- result[0]: Displays the ADF statistic.
Python
def check_stationarity(timeseries):
result = adfuller(timeseries, autolag='AIC')
p_value = result[1]
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {p_value}')
print('Stationary' if p_value < 0.05 else 'Non-Stationary')
check_stationarity(monthly_sales['Sales'])
Output:
ADF Statistic: -4.493767844002665
p-value: 0.00020180198458237758
Stationary
6. Identifying Model Parameters
We can identify the SARIMA model parameters (p, d, q, P, D, Q, s) using Autocorrelation (ACF) and Partial Autocorrelation (PACF) plots. These plots help in determining the order of the model components.
- plot_acf(): Plots the Autocorrelation Function (ACF) to visualize correlations between lags.
- plot_pacf(): Plots the Partial AutoCorrelation Function (PACF) to visualize partial correlations between lags.
Python
plot_acf(monthly_sales)
plot_pacf(monthly_sales)
plt.show()
Output:
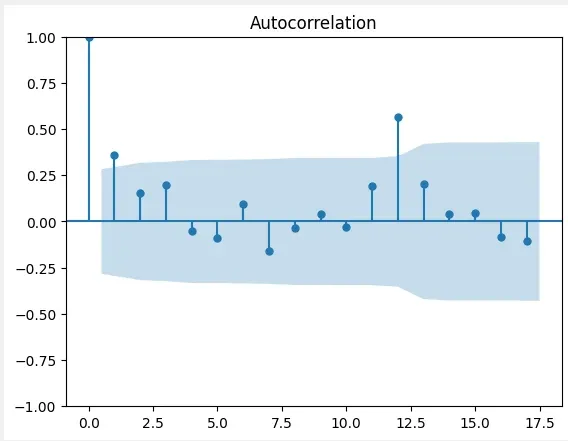 ACF
ACF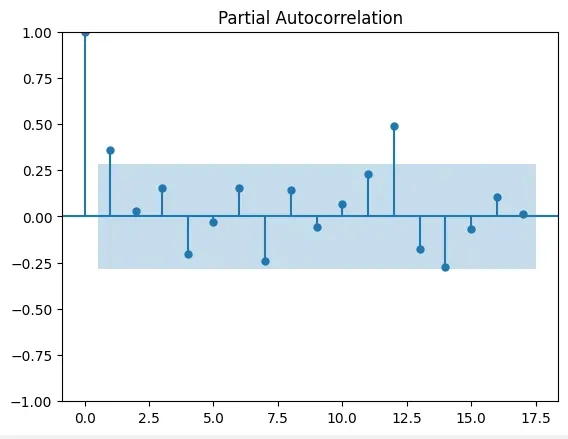 PACF
PACF7. Fitting the SARIMA Model
Once we have identified the model parameters, we can fit the SARIMA model using the SARIMAX function.
- SARIMAX(): Initializes the SARIMA model with specified non-seasonal and seasonal parameters.
- fit(): Fits the SARIMA model to the historical data.
Python
p, d, q = 1, 1, 1
P, D, Q, s = 1, 1, 1, 12
model = SARIMAX(monthly_sales, order=(p, d, q), seasonal_order=(P, D, Q, s))
results = model.fit()
8. Generating Forecasts
With the SARIMA model fitted, we can forecast future sales values. For example, forecasting the next 12 months.
- result.forecast(steps=forecast_periods): Generates the forecast for future time steps.
- plt.plot(): Plots the observed and forecasted data.
- plt.legend(): Adds a legend to the plot to label observed and forecasted data.
Python
forecast_periods = 12
forecast = results.forecast(steps=forecast_periods)
plt.figure(figsize=(10, 6))
plt.plot(monthly_sales, label='Observed')
plt.plot(forecast, label='Forecast', color='red')
plt.title("Sales Forecast")
plt.xlabel("Date")
plt.ylabel("Sales")
plt.legend()
plt.show()
Output:
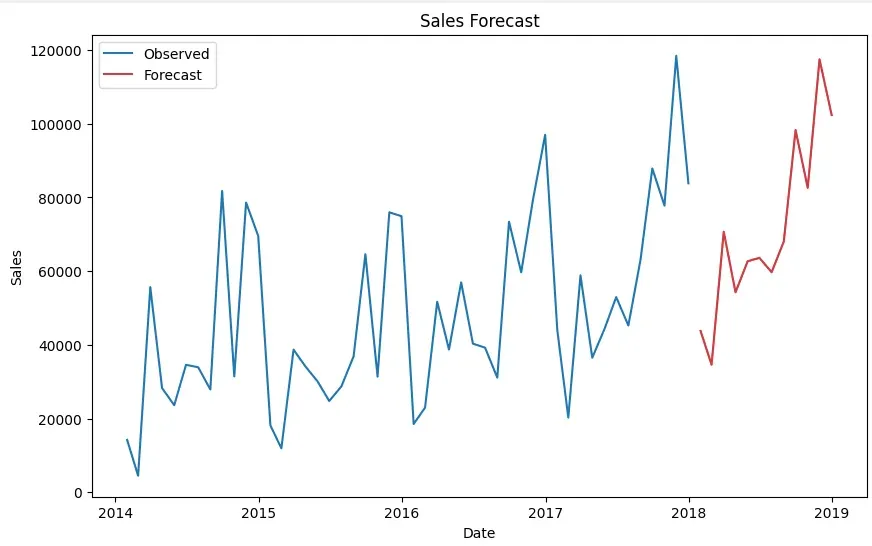 Forecasts
Forecasts9. Evaluating the Model
We evaluate the model’s forecast accuracy using Mean Absolute Error (MAE) and Mean Squared Error (MSE).
- mean_absolute_error(): Computes the Mean Absolute Error (MAE) to measure prediction accuracy.
- mean_squared_error(): Computes the Mean Squared Error (MSE) to assess model performance.
Python
observed = monthly_sales[-forecast_periods:]
mae = mean_absolute_error(observed, forecast_mean)
mse = mean_squared_error(observed, forecast_mean)
print(f'MAE: {mae}')
print(f'MSE: {mse}')
Output:
MAE: 10611.591984026598
MSE: 151953342.15188608
Explore
Machine Learning Basics
Python for Machine Learning
Feature Engineering
Supervised Learning
Unsupervised Learning
Model Evaluation and Tuning
Advanced Techniques
Machine Learning Practice