Open In App

Statistics For Machine Learning

Last Updated : 11 Sep, 2025
Comments
Improve
Suggest changes
6 Likes
Like
Report

Statistics for Machine Learning is the study of collecting, analyzing and interpreting data to help build better machine learning models. It provides the mathematical foundation to understand data patterns, make predictions and evaluate model performance.

  • It helps in understanding data distribution, variability and selecting the most useful features.
  • It is used to validate model results and make decisions under uncertainty using hypothesis tests, confidence intervals and Bayesian methods.
how_statistics_is_used_in_machine_learning
Machine Learning Statistics

Why Learn Statistics for Machine Learning

  • Understand the data before training models.
  • Choose the right algorithms for specific problems.
  • Evaluate model accuracy and performance.
  • Handle uncertainty and variability in real-world data.

Applications of Statistics in Machine Learning

Statistics is a key component of machine learning, with broad applicability in various fields.

  • Feature Engineering: selecting and transforming useful variables.
  • Image Processing: analyzing patterns, shapes and textures.
  • Anomaly Detection: spotting fraud or equipment failures.
  • Environmental Studies: modeling land cover, climate and pollution.
  • Quality Control: identifying defects in manufacturing.

Types of Statistics

There are commonly two types of statistics, which are discussed below:

  • Descriptive Statistics: "De­scriptive Statistics" helps us simplify and organize big chunks of data. This makes large amounts of data easier to understand.
  • Inferential Statistics: "Inferential Statistics" is a little different. It uses smaller data to draw conclusions about a larger group. It helps us predict and draw conclusions about a population.

Descriptive Statistics

Descriptive statistics summarize and describe the features of a dataset, providing a foundation for further statistical analysis.

Mean

Median

Mode

Mean is the sum of all values divided by the total number of values.
Mean μ = Sum of Values \ Number of Values

Median is the middle value of sorted data

For odd number of data points:

Median = (\frac{n+1}{2})^{th}

For even number of data points:

Median = Average of (\frac{n}{2})^{th} value and its next value

Mode is the most frequently occurring value in the dataset.


Measures of Dispersion

  • Range: The difference between the maximum and minimum values.
  • Variance: The average squared deviation from the mean, representing data spread.
  • Standard Deviation: The square root of variance, indicating data spread relative to the mean.
  • Interquartile Range: The range between the first and third quartiles, measuring data spread around the median.

Measures of Shape

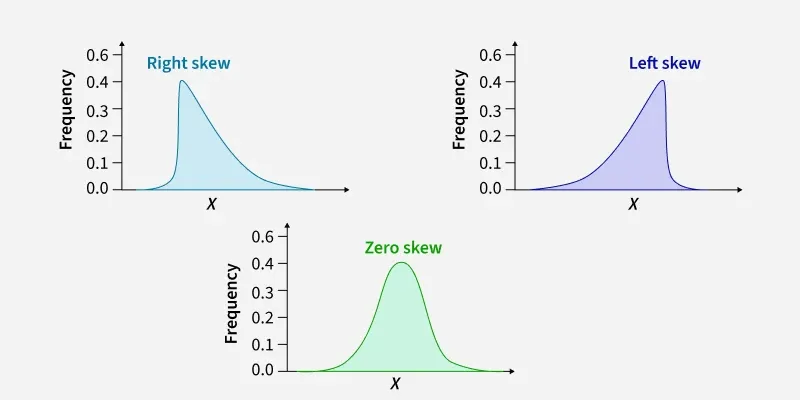skewness
Skewness
  • Kurtosis: Measures the peakedness of the data distribution.
Types-of-Skewed-data
Types of Skewed data

Inferential Statistics

Inferential statistics involve making predictions or inferences about a population based on a sample of data.

Population and Sample

  • Population: The entire group being studied.
  • Sample: A subset of the population used for analysis.

Estimation

Hypothesis Testing

Hypothesis testing is a method that compares two opposite assumptions about a population and uses data from a sample to determine which assumption is more likely to be true.

Covariance and Correlation

Covariance

Correlation

Covariance measures the degree to which two variables change together.

Cov(x,y) = \frac{\sum(X_i-\overline{X})(Y_i - \overline{Y})}{n}

Correlation shows how strongly and in which direction two variables are related. Its coefficient ranges from -1 to 1, where positive means they move together and negative means they move oppositely.

Pearson's correlation coefficient is given by:

\rho(X, Y) = \frac{cov(X,Y)}{\sigma_X \sigma_Y}

Visualization Techniques

Regression Analysis

Understanding relationships between variables is important in machine learning.

Probability Theory

Probability theory forms the backbone of statistical inference, aiding in quantifying uncertainty and making predictions based on data.

Basic Concepts

Common Probability Distributions

Bayesian Statistics

Bayesian statistics combine prior knowledge (what we already believe) with new data (current evidence) to update our understanding.

Bayes' Theorem is a fundamental concept in probability theory that relates conditional probabilities. It is named after the Reverend Thomas Bayes, who first introduced the theorem. Bayes' Theorem is a mathematical formula that provides a way to update probabilities based on new evidence.

Formula:

P(A \mid B) = \frac{P(B \mid A) \times P(A)}{P(B)}

Where

  • P(A∣B): The probability of event A given that event B has occurred (posterior probability).
  • P(B∣A): The probability of event B given that event A has occurred (likelihood).
  • P(A): The probability of event A occurring (prior probability).
  • P(B): The probability of event B occurring.

Related Articles


D

deepanshukq4p4
Improve
Article Tags :

Explore

Lightbox