Predicates and Quantifiers

Predicates and Quantifiers are fundamental concepts in mathematical logic, essential for expressing statements and reasoning about the properties of objects within a domain. These concepts are widely used in computer science, engineering, and mathematics to formulate precise and logical statements.

This article explores the definitions, types, and applications of predicates and quantifiers in engineering.

Predicates

A predicate is a statement that contains variables and becomes a proposition when specific values are substituted for those variables. Predicates express properties or relations among objects. Example:

P(x) = "x is an even number"

When x=2, P(2) is True.

When x=3, P(3) is False.

Quantifiers

Quantifiers specify the extent to which a predicate is true over a range of elements. The two main types of quantifiers are:

Universal Quantifier

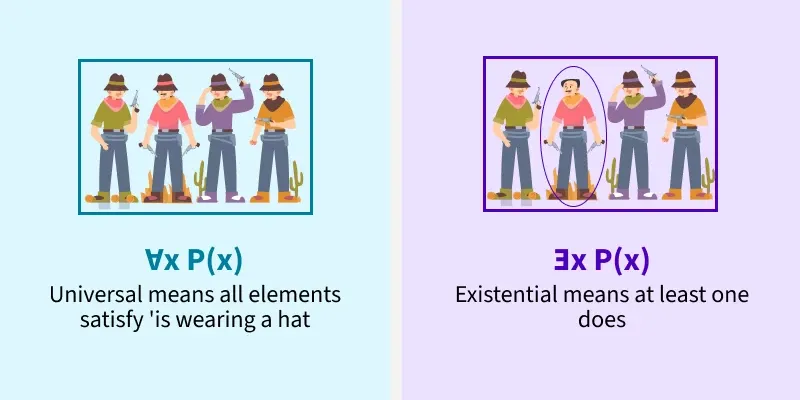
The universal quantifier (∀) indicates that a predicate is true for all elements in a given domain. Example:

∀ x ∈N, P(x)

Translation: "For all natural numbers xxx, xxx is even."

Existential Quantifier

The existential quantifier (∃) indicates that there exists at least one element in a given domain for which the predicate is true. Example:

∃x∈N, P(x)

Translation: "There exists a natural number x such that x is even."

Sample Examples - Predicates and Quantifiers

Example 1: Let P(x) be the predicate "x > 5" where x is a real number.

P(7) is true because 7 > 5

P(3) is false because 3 is not > 5

Example 2: Let Q(x,y) be the predicate "x + y = 10" where x and y are integers.

Q(3,7) is true because 3 + 7 = 10

Q(4,5) is false because 4 + 5 ≠ 10

Quantifiers:

There are two main types of quantifiers:

Universal Quantifier (∀): "for all"

Existential Quantifier (∃): "there exists"

Example 3: Let R(x) be the predicate "x² ≥ 0" where x is a real number.

The statement ∀x R(x) is true because for all real numbers, their square is always non-negative.

Example 4: Let S(x) be the predicate "x² = 4" where x is a real number.

The statement ∃x S(x) is true because there exist real numbers (2 and -2) whose square is 4.

Example 5: Consider the predicate P(x,y): "x + y = 0" where x and y are integers.

The statement ∀x ∃y P(x,y) is true because for any integer x, we can always find an integer y such that their sum is 0 (y would be -x).

Example 6: Let Q(x) be the predicate "x is prime" where x is a positive integer.

The statement ∀x Q(x) is false because not all positive integers are prime.

The statement ∃x Q(x) is true because there exist prime numbers (e.g., 2, 3, 5, 7, etc.).

Example 7: Let R(x,y) be the predicate "x < y" where x and y are real numbers.

The statement ∀x ∀y R(x,y) is false because it's not true that every real number is less than every other real number.

The statement ∃x ∃y R(x,y) is true because we can find two real numbers where one is less than the other (e.g., 1 < 2).

Example 8: Let P(x) be the predicate "x is divisible by 3" where x is an integer. Determine the truth value of ∀x P(x) and ∃x P(x).

∀x P(x) is false because not all integers are divisible by 3 (e.g., 4 is not divisible by 3).

∃x P(x) is true because there exist integers divisible by 3 (e.g., 0, 3, 6, 9, etc.).

Example 9: Let Q(x,y) be the predicate "x + y > 10" where x and y are real numbers. Determine the truth value of ∀x ∃y Q(x,y).

Solution:

∀x ∃y Q(x,y) is true.

For any real number x, we can always find a y such that x + y > 10.

We can choose y = 11 - x, which will always make x + y > 10 regardless of the value of x.

Example 10: Let R(x) be the predicate "x is a vowel" where x is a letter in the English alphabet. Write the following statement using predicate logic: "There is a vowel in the English alphabet."

The statement can be written as: ∃x R(x)

This reads as "There exists an x such that x is a vowel."

Unsolved Problems on Predicates and Quantifiers

1. Let P(x) be the predicate "x² - 1 = 0" where x is a real number. Determine the truth value of ∃x P(x).

2. Let Q(x,y) be the predicate "x < y" where x and y are integers. What does ∀x ∃y Q(x,y) mean in words?

3. Let R(x) be the predicate "x is even" where x is an integer. Write the statement "All integers are even" using predicate logic.

4. Let S(x) be the predicate "x is a mammal" and T(x) be "x can fly" where x is an animal. How would you express "Some mammals can fly" using predicate logic?

5. Let P(x,y) be the predicate "x is the parent of y" where x and y are people. Express "Everyone has a parent" using predicate logic.

6. Let Q(x) be the predicate "x is prime" where x is a positive integer. What is the negation of ∀x Q(x)?

7. Let R(x,y) be the predicate "x + y = 10" where x and y are integers. Is the statement ∀x ∀y R(x,y) true or false? Explain why.

8. Let S(x) be the predicate "x is a multiple of 5" where x is an integer. Express the statement "There is no integer that is a multiple of 5" using predicate logic.

9. Let T(x,y) be the predicate "x is taller than y" where x and y are people. Express the statement "Nobody is taller than themselves" using predicate logic.

10. Let P(x) be the predicate "x is a planet in our solar system" where x is a celestial body. How would you express "There are exactly 8 planets in our solar system" using predicate logic?

Differences Between Predicates and Quantifiers