Angle relationships are a fundamental aspect of Geometry that every student must understand. These relationships describe how different angles interact with each other when formed by the intersecting lines, rays or within the various geometric shapes. Understanding angle relationships is crucial for solving problems in Geometry, trigonometry and even in real-life applications such as in Engineering and architecture.
What are Angles in Geometry?
In geometry, angles are formed when two rays or line segments meet at a common endpoint, known as the vertex.
The space between the two rays is measured in degrees (°), which indicates the rotation from one ray to the other around the vertex. Angles are fundamental in understanding shapes, structures, and various geometric properties. They are widely used in fields such as architecture, engineering, and trigonometry.
Types of Angles
Angles are classified based on their measurements:
- Acute Angle: Less than 90°
- Right Angle: Exactly 90°
- Obtuse Angle: More than 90° but less than 180°
- Straight Angle: Exactly 180°
- Reflex Angle: More than 180° but less than 360°
- Complete Angle: Exactly 360°.
Various Angle Relationships
Various angle relationships are:
- Complementary Angles
- Supplementary Angles
- Adjacent Angles
- Linear Pair of Angles
- Vertical Angles
- Angle Sum Property
- Angle Relationships in Parallel and Transversal Line
Let's discuss these in detail.
Complementary Angles
The Two angles are complementary if the sum of their measures is 90°.
Example: If ∠PQR = 30° and ∠RST = 60° then ∠PQR and ∠RST are complementary angles.
Properties:
- The Complementary angles do not necessarily have to be adjacent.
- Each angle is known as the complement of the other.
Supplementary Angles
The Two angles are supplementary if the sum of their measures is 180°.
Example: If ∠ABC = 110° and ∠XYZ = 70° then ∠ABC and ∠XYZ are supplementary angles.
Properties:
- The Supplementary angles can either be adjacent or non-adjacent.
- Each angle is known as the supplement of the other.
Adjacent Angles
The Two angles are adjacent if they share a common vertex and common side but do not overlap.
Example: Consider angles ∠ABC and ∠CBD that share a common side BC. These two angles are adjacent.
Properties
- The Adjacent angles can form complementary or supplementary angles depending on their measurements.
- The sum of adjacent angles on the straight line is always 180°.
Linear Pair of Angles
A linear pair of angles is a pair of the adjacent angles formed when two lines intersect.
Example: If ∠ABC and ∠CBD are on a straight line with the common side then they form a linear pair.
Properties:
- The angles in the linear pair are supplementary.
- The sum of the angles in the linear pair is always 180°.
Vertical Angles
When two lines intersect the opposite angles formed are called vertical angles.
Example: If two lines intersect and form angles of 85° the opposite angles are also 85°.
Properties:
- Vertical angles are always equal.
- They are formed in pairs.
Angle Sum Property
The angle sum property states that the sum of the all angles in the triangle is always 180°.
Example: In a triangle ABC if ∠A = 50°, ∠B = 60° then ∠C = 70° because 50° + 60° + 70° = 180°.
Properties:
- This property applies to the all types of the triangles whether they are acute obtuse or right-angled.
- It is a crucial concept in solving the many geometric problems.
Angle Relationships in Parallel and Transversal Line
- Alternate Interior Angles: When two parallel lines are intersected by a transversal, the angles on opposite sides of the transversal but inside the parallel lines are called alternate interior angles. They are equal.
- Example: ∠1 and ∠2 on opposite sides of the transversal.
- Alternate Exterior Angles: These are the angles formed outside two parallel lines on opposite sides of a transversal. They are equal.
- Example: ∠3 and ∠4 outside parallel lines.
- Corresponding Angles: When two parallel lines are intersected by a transversal, the angles in the same position on both lines are corresponding angles, and they are equal.
- Example: ∠5 and ∠6 at the same location on each line.
- Interior Angles of a Polygon: The angles inside a polygon. The sum of the interior angles of an n-sided polygon is given by (n−2)×180∘(n-2) \times 180^\circ(n−2)×180∘.
- Example: The sum of the interior angles of a triangle is 180∘180^\circ180∘.
- Exterior Angles of a Polygon: The angles formed outside the polygon when one side is extended. The sum of the exterior angles of any polygon is always 360∘360^\circ360∘.
- Example: The exterior angles of a square add up to 360°.
Solved Examples with Solutions: Angle Relationships
Example 1: If one angle measures 40° what is the measure of its complementary angle?
Solution:
The complementary angle is found by the subtracting the given angle from 90°.
Complementary Angle=90°−40°=50°
So, the complementary angle is 50°.
Example 2: Two angles are supplementary. If one angle measures 125° what is the measure of the other angle?
Solution:
The supplementary angle is found by the subtracting the given angle from 180°.
Supplementary Angle=180°−125°=55°
So, the supplementary angle is 55°.
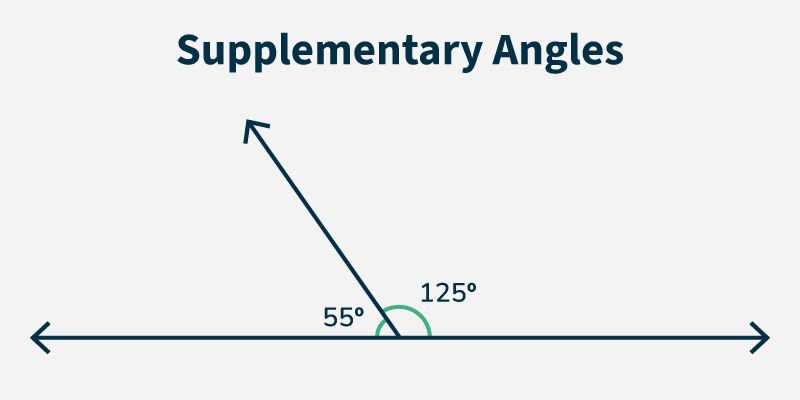 Supplementary Angles
Supplementary Angles
Example 3: The Two lines intersect forming one angle of 85°. What is the measure of the vertically opposite angle?
Solution:
The Vertically opposite angles are always equal.
Vertically Opposite Angle=85°
So, the vertically opposite angle is 85°.
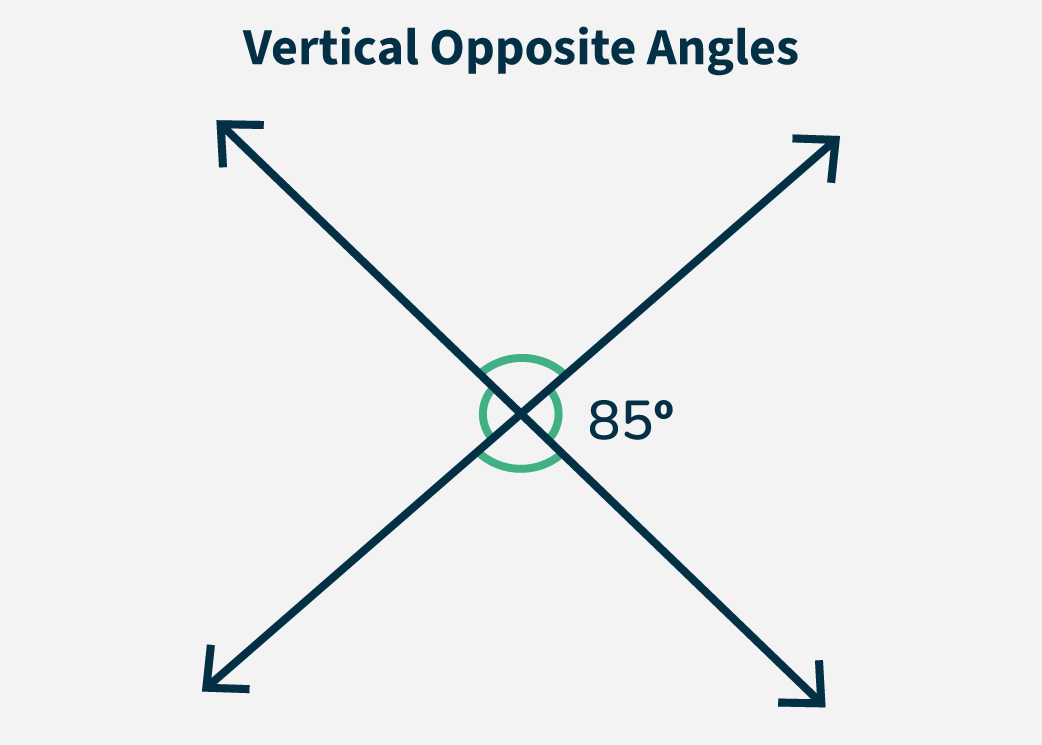 Vertical Opposite Angles
Vertical Opposite Angles
Example 4: In a triangle, two angles measure 45° and 65°. Find the measure of the third angle.
Solution:
The sum of the all angles in a triangle is 180°.
Third Angle=180°−(45°+65°)=180°−110°=70°
So, the third angle measures 70°.
 Angle sum property of a Triangle
Angle sum property of a Triangle
Example 5: If one angle in a linear pair measures 120° what is the measure of the other angle?
Solution:
The angles in the linear pair are supplementary.
Other Angle = 180° − 120° = 60°
So, the measure of the other angle is 60°.
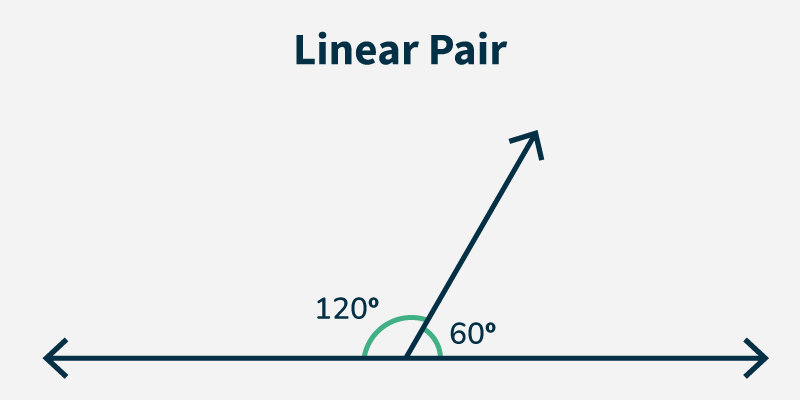 Linear Pair
Linear Pair
Practical Questions: Angle Relationships
Q1: If two complementary angles have a ratio of 2:3. what are their measures?
Q2: The angles of a triangle are in the ratio 1:2:3. Determine the measure of each angle.
Q3: Two supplementary angles differ by 40°. Find the measure of each angle.
Q4: Find the measure of an angle if it is 15° less than its supplement.
Q5: If two angles are vertically opposite and one of them measures 76°. what is the measure of the other angle?
Q6: In a triangle, the exterior angle measures 100° and one of the interior opposite angles measures 40°. Find the other interior opposite angle.
Q7: Two angles are in a linear pair and one of the angles is four times the other. Find the measure of each angle.
Q8: The measures of two supplementary angles are in the ratio 7:11. Find the measures of the angles.
Q9: Find the angles of a triangle if the difference between greatest and the smallest angle is 30° and middle angle is twice the smallest angle.
Q10: A pair of adjacent angles is formed when two lines intersect. If one of the angles measures 65°. what is the measure of the other three angles?
Answer Key
- 36° and 54°
- 30°, 60°, and 90°
- 70° and 110°
- 82.5°
- 76°
- 60°
- 36° and 144°
- 70° and 110°
- 30°, 60°, and 90°
- 65°, 115°, and 115°
Conclusion
Understanding angle relationships is a crucial part of mastering geometry. These relationships form the basis for the solving more complex geometric problems and are applicable in the various fields such as the architecture, engineering and design. By recognizing and applying these relationships students can enhance their problem-solving skills and develop a deeper understanding of the geometry.
Read More,
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice