Area of Isosceles Triangle

Area of Isosceles triangle is the space enclosed by the sides of a triangle. The general formula for finding the area of the isosceles triangle is given by half the product of the base and height of the triangle. Other than this different formulas are used to find the area of triangles. Triangles are classified depending on their sides, different types of triangles based on sides are given below:

1. Equilateral Triangle: Triangle with all three sides equal.
2. Isosceles Triangle: Triangle with any two sides equal.
3. Scalene Triangle: Triangle with all sides unequal.

What is an Isosceles Triangle?

Isosceles triangle is a type of triangle with two equal sides. The two angles opposing the two equal sides are also equal. Assume that in a triangle △ABC, if the sides AB and AC are equal, ABC is an isosceles triangle with ∠B = ∠C. The isosceles triangle is described by the theorem "If the two sides of a triangle are equal, then the angle opposite to them are likewise equal".

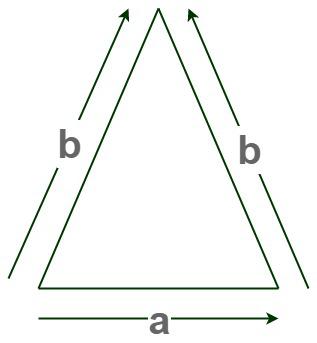
Properties of Isosceles triangle

• Isosceles triangle has two equal sides and are known as the legs and the angle between those equal sides is called the vertex angle or apex angle.
• The side opposite the vertex angle is called the base.
• The angle opposite to equal sides are also equal and are known as base angles.
• The perpendicular drawn from the vertex angle bisects the base and the vertex angle.

Formulas for Area of Isosceles Triangle

Area of an isosceles triangle is given by the formula listed below:

Area = ½ × base × Height

Also,

Perimeter of isosceles triangle (P) = 2a + b
Altitude of isosceles triangle (h) = √(a² − b²/4)

where, a, b are the sides of a isosceles triangle.

Formulas:

The following table contains various formulas are used to find the Area of the Isosceles Triangle . Few of the most used formulas for the area of the isosceles triangle are listed below:

Area of Isosceles Triangle Formula with Sides

When the length of equal sides and the length of the base of an isosceles triangle are given, then the height of the triangle can also be calculated by the given formula:

Altitude of an Isosceles Triangle = √(a² − b²/4)

Area of Isosceles Triangle (if all sides are given) = ½[√(a² − b² /4) × b]

Where,

• b = base of the isosceles triangle, and
• a = length of the two equal sides.

Derivation for Area of Isosceles Triangle 

If the lengths of an isosceles triangle's equal sides and base are known, the triangle's height or altitude may be computed. The formula for calculating the area of an isosceles triangle with sides is as follows:

Isosceles triangle area = ½[√(a² − b² /4) × b]

where,

b = the isosceles triangle's base
a = the length of two equal sides

From the above figure, we have,

AB = AC = a (sides of equal length)

BD = DC = ½ BC = ½ b (Perpendicular from the vertex angle ∠A bisects the base BC)

Using Pythagoras theorem on ΔABD,

a² = (b/2)² + (AD)²

AD = \sqrt{a^2 - \frac{b^2}{4}}

The altitude of an isosceles triangle = \sqrt{a^2 - \frac{b^2}{4}}

It is known that the general formula of area of the triangle is, Area = ½ × b × h

Substituting value for height, we get

Area of isosceles triangle = ½[√(a² − b² /4) × b]

Area of Isosceles Triangle Using Heron’s Formula

The area of an isosceles triangle formula can be easily derived using Heron’s formula as explained in the following steps. Heron's formula is used to find the area of a triangle when the measurements of its 3 sides are given.

Derivation:

The Heron's formula to find the area, A of a triangle whose sides are a,b, and c is:

A = √s(s-a)(s-b)(s-c)

where,

• a, b, and c are the sides of the triangle.
• s is the semi perimeter of the triangle.

We know that the perimeter of a triangle with sides a, b, and c is a + b + c. Here, s is half of the perimeter of the triangle, and hence, it is called semi-perimeter.

Then, the semi-perimeter is:

s = (a + b + c)/2

as b = a,

s = ½(a + a + b)

⇒ s = ½(2a + b) = a + (b/2)

now,

Area of Isosceles Triangle = √[s(s−a)(s−b)(s−c)]

Area = √[s (s−a)² (s−b)]

Area = (s−a) × √[s (s−b)]

Substituting the value for “s”

⇒ Area = (a + b/2 − a) × √[(a + b/2) × ((a + b/2) − b)]

⇒ Area = b/2 × √[(a + b/2) × (a − b/2)]

Area of isosceles triangle = b/2 × √(a² − b²/4) square units

where,

• b = base of the isosceles triangle
• a = length of the two equal sides

Area of Right Angled Isosceles Triangle

Area of an Isosceles Right Triangle is given by the formula 

Formula for Isosceles Right Triangle Area= ½ × a²

Derivation:

Area of an isosceles triangle (Area) = ½ ×base × height

⇒ Area = ½ × a × a = a²/2

Perimeter of Isosceles Right Triangle P = (2+√2)a

Derivation:

Perimeter of an isosceles right triangle is the sum of all the sides of an isosceles right triangle.

Let the two equal sides be a. By Pythagoras theorem the unequal side is a√2.

Perimeter of isosceles right triangle = a+a+a√2
⇒ Perimeter of isosceles right triangle = 2a+a√2
⇒ Perimeter of isosceles right triangle = a(2+√2)
⇒ Perimeter of isosceles right triangle = a(2+√2)

Area of Isosceles Triangle using Trigonometry

When the Length of the two Sides and the Angle between them are given,

A = ½ × b × c × sin(α)

Where,

• b, c are sides of a given triangle, and
• α is the angle between them.

When the two angles and sides between them are given,

A = [c²×sin(β)×sin(α)/ 2×sin(2π−α−β)]

Where,

• c is sides of a given triangle, and
• α, β is the angle associated with them.

Related Articles

• Area of Square
• Area of Rhombus
• Area of Rectangle

Solved Examples on Area of Isosceles Triangle

Example 1: Find the area of an isosceles triangle with an equal side of 13 cm and a base of 24 cm.

Solution:

We have, a = 13 and b = 24.

Area of isosceles triangle is given by, 

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{13^2 - \frac{24^2}{4}}\right) × 24

⇒ A = 1/2 × 5 × 24

⇒ A = 60 cm²

Example 2: Find the area of an isosceles triangle with an equal side of 10 cm and a base of 12 cm.

Solution:

We have, a = 10 and b = 12.

Area of isosceles triangle is given by,

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{10^2 - \frac{12^2}{4}}\right) × 12

⇒ A = 1/2 × 8 × 12

⇒ A = 48 cm²

Example 3: Find the area of an isosceles triangle with an equal side of 5 cm and a base of 6 cm.

Solution:

We have, a = 5 and b = 6.

Area of isosceles triangle is given by,

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{5^2 - \frac{6^2}{4}}\right) × 6

⇒ A = 1/2 × 4 × 6

⇒ A = 12 cm²

Example 4: Find the area of an isosceles triangle with an equal side of 15 cm and a base of 24 cm.

Solution:

We have, a = 15 and b = 24.

Area of isosceles triangle is given by,

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{15^2 - \frac{24^2}{4}}\right) × 24

⇒ A = 1/2 × 9 × 24

⇒ A = 108 cm²

Example 5: Find the area of an isosceles triangle with an equal side of 17 cm and a base of 30 cm.

Solution:

We have, a = 17 and b = 30.

Area of isosceles triangle is given by,

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{17^2 - \frac{30^2}{4}}\right) × 30

⇒ A = 1/2 × 8 × 30

⇒ A = 120 cm²

Example 6: Find the area of an isosceles triangle with an equal side of 20 cm and a base of 24 cm.

Solution:

We have, a = 20 and b = 24.

Area of isosceles triangle is given by,

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{20^2 - \frac{24^2}{4}}\right) × 24

⇒ A = 1/2 × 16 × 24

⇒ A = 192 cm²

Example 7: Find the area of an isosceles triangle with an equal side of 25 cm and a base of 30 cm.

Solution:

We have, a = 25 and b = 30.

Area of isosceles triangle is given by,

A = \frac{1}{2} ×\left(\sqrt{a^2 - \frac{b^2}{4}}\right) × b

⇒ A = \frac{1}{2} ×\left(\sqrt{25^2 - \frac{30^2}{4}}\right) × 30

⇒ A = 1/2 × 20 × 30

⇒ A = 300 cm²

Conclusion

Area of isosceles triangle, as well as the general area of any triangle, can be calculated using a variety of formulas depending on the known parameters. Whether using the basic base-height method, Heron’s formula, or trigonometric approaches, each method provides a reliable way to determine the area based on the isosceles triangle’s unique properties. Understanding these formulas not only simplifies geometric calculations but also enhances problem-solving skills in various mathematical contexts.