Question 1: Find the equation of the straight lines passing through the origin and making an angle of 45° with the straight line √3x+y = 11.
Solution:
As line 1 passes through origin, there won't be any intercept, and it will be in the form of y = mx (m as slope)
For line 2: √3x+y = 11, slope is M = -√3
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 45°, m=m and M = -√3
tan 45° = |\frac{-\sqrt{3}-m}{1+m(-\sqrt{3})}|
1 = |\frac{-\sqrt{3}-m}{1-\sqrt{3}m}|
We will have two cases,
1 = \frac{-\sqrt{3}-m}{1-\sqrt{3}m} and 1 = -\frac{-\sqrt{3}-m}{1-\sqrt{3}m}
1-√3m = -√3-m and 1-√3m = √3+m
√3m-m = 1+√3 and √3m+m = 1-√3
m = \frac{1+\sqrt{3}}{\sqrt{3}-1} and m = \frac{1-\sqrt{3}}{\sqrt{3}+1}
By rationalizing, we get
m = \frac{(1+\sqrt{3})^2}{3-1} and m = -\frac{(1-\sqrt{3})^2}{3-1}
m = \frac{1+3+2\sqrt{3}}{2} and m = -\frac{1+3-2\sqrt{3}}{2}
m = 2+√3 and m = -(2-√3)
m = √3+2 and m = √3-2
Hence, the equation of line will be,
y = (√3+2)x and y = (√3-2)x
Question 2: Find the equation to the straight lines which pass through the origin and are inclines at an angle of 75° to the straight line x+y+√3(y-x)=a.
Solution:
As line 1 passes through origin, there won't be any intercept and it will be in the form of y = mx (m as slope)
For line 2: x+y+√3(y-x)=a,
x+y+√3y-√3x=a
x(1-√3)+y(1+√3)=a
slope is M = \frac{\sqrt{3}-1}{\sqrt{3}+1}
After rationalizing, we get
M = \frac{(\sqrt{3}-1)^2}{3-1} = \frac{(3+1-2\sqrt{3})^2}{2} = 2-√3
Here, it is given that these two lines make an angle of 75° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 75°, m=m and M = 2-√3
tan 75° = |\frac{(2-√3)-m}{1+m(2-√3)}|
tan (45°+30°)= |\frac{(2-√3)-m}{1+m(2-√3)}|
Using the trigonometric identity,
tan (a+b) = \frac{tan \hspace{0.1cm}a + tan\hspace{0.1cm} b}{1-(tan\hspace{0.1cm} a) (tan\hspace{0.1cm} b)}
\frac{tan 45\degree + tan 30\degree}{1-(tan 45\degree) (tan 30\degree)} = |\frac{(2-\sqrt{3})-m}{1+m(2-\sqrt{3})}|
\frac{1 + \frac{1}{\sqrt{3}}}{1-(1) (\frac{1}{\sqrt{3}})} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{\frac{√3+1}{\sqrt{3}}}{\frac{√3-1}{\sqrt{3}}} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{√3+1}{√3-1} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{(√3+1)^2}{3-1} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ \frac{(3+1+2√3)^2}{2} = |\frac{(2-√3)-m}{1+m(2-√3)}|\\ 2+√3 = |\frac{(2-√3)-m}{1+m(2-√3)}|
We will have two cases,
2+√3 = \frac{(2-\sqrt{3})-m}{1+m(2-\sqrt{3})} and 2+√3 = -\frac{(2-\sqrt{3})-m}{1+m(2-\sqrt{3})}
(2+√3)(1+m(2-√3)) = 2-√3-m and (2+√3)(1+m(2-√3)) = -(2-√3-m)
(2+√3+m(22-(√3)2) = 2-√3-m and (2+√3+m(22-(√3)2) = √3-2+m
2+√3+m(4-3) = 2-√3-m and 2+√3+m(4-3) = √3-2+m
2+√3+m+m = 2-√3 and 2+√3+m-m = √3-2
2m = -2-√3+2-√3 and 2+√3 = √3-2
2m = -2√3 and m is not defined
m = -√3 and m is not defined
Hence, the equation of line will be,
y = -√3x and x = 0
Question 3: Find the equation of the straight lines passing through (2,-1) and making an angle of 45° with the line 6x+5y-8=0.
Solution:
As line 1 passes through (2,-1), then it will be in the form of
y-(-1) = m(x-2) (m as slope)
y+1 = m(x-2)
For line 2: 6x+5y-8=0
5y = -6x + 8
y = \frac{-6}{5}x + \frac{8}{5}
slope is M = \frac{-6}{5}
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 45°, m=m and M = \frac{-6}{5}
tan 45° = |\frac{\frac{-6}{5}-m}{1+m(\frac{-6}{5})}|
1 = |\frac{\frac{-6-5m}{5}}{1-m(\frac{6}{5})}|\\ 1 = |\frac{\frac{-6-5m}{5}}{\frac{5-6m}{5}}|\\ 1 = |\frac{-6-5m}{5-6m}|
We will have two cases,
1 = \frac{-6-5m}{5-6m} and 1 = -\frac{-6-5m}{5-6m}
5-6m = -6-5m and 5-6m = -(-6-5m)
6m-5m = 5+6 and 5-6m = 5m+6
m = 11 and 5m+6m = 5-6
m = 11 and m = \frac{-1}{11}
Hence, the equation of line will be,
y+1 = 11(x-2) and y+1 = \frac{-1}{11}(x-2)
11x-y-23=0 and 11y+x+9 = 0
Question 4: Find the equation to the straight lines which pass through the point (h,k) and are inclined at angle tan-1 m to the straight line y=mx+c.
Solution:
As line 1 passes through (h,k), then it will be in the form of
y-(k) = M(x-h) (M as slope)
For line 2: y=mx+c (m as slope)
Here, it is given that these two lines make an angle of tan-1 m between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = tan-1 m,
tan (tan-1 m) = |\frac{M-m}{1+mM}|
m = |\frac{M-m}{1+mM}|
We will have two cases,
m = \frac{M-m}{1+mM} and m = -\frac{M-m}{1+mM}
m(1+mM) = M-m and m(1+mM) = -(M-m)
m+m2M = M-m and m+m2M = m-M
2m = M-m2M and m2M = -M
M = \frac{2m}{1-m^2} and M = 0
Hence, the equation of line will be,
y-(k) = 0(x-h) and y-k = \frac{2m}{1-m^2}(x-h)
y-k = 0 and (y-k)(1-m2) = (2m)(x-h)
Question 5: Find the equation to the straight lines passing through the point (2,3) and inclined at 45° to the line 3x+y-5=0.
Solution:
As line 1 passes through (2,3), then it will be in the form of
y-3 = M(x-2) (M as slope)
For line 2: 3x+y-5=0
y = -3x+5
slope m = -3
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 45°,
tan 45° = |\frac{M-(-3)}{1+(-3)M}|
1 = |\frac{M+3}{1-3M}|
We will have two cases,
1 = \frac{M+3}{1-3M} and 1 = -\frac{M+3}{1-3M}
1-3M = M+3 and 1-3M = -(M+3)
M+3M = 1-3 and 1-3M = -M-3
4M = -2 and 3M-M = 1+3
M = \frac{-2}{4} and 2M = 4
M = \frac{-1}{2} and M = 2
Hence, the equation of line will be,
y-3 = \frac{-1}{2}(x-2) and y-3 = 2(x-2)
2y-6 = -(x-2) and y-3 = 2x-4
x+2y-8=0 and 2x-y-1=0
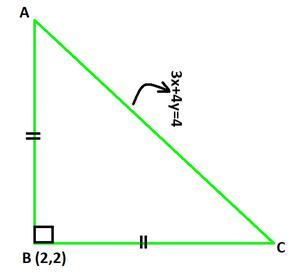
Question 6: Find the equation to the sides of an isosceles right-angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2,2).
Solution:
As △ABC is an isosceles right angled triangle at B.
∠A = ∠C = 45°
We can say that, AB and BC makes 45° with AC.
Let the slope of AB as m1 and BC as m2.
AB: (y-2) = m1(x-2)
BC: (y-2) = m2(x-2)
Slope of AC : 3x+4y=4
y = \frac{-3}{4}x + 1
Slope of AC is \frac{-3}{4}.
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 45°, and M = \frac{-3}{4}
tan 45° = |\frac{\frac{-3}{4}-m}{1+m(\frac{-3}{4})}|
1 = |\frac{\frac{-3-4m}{4}}{1-m(\frac{3}{4})}|\\ 1 = |\frac{\frac{-3-4m}{4}}{\frac{4-3m}{4}}|\\ 1 = |\frac{-3-4m}{4-3m}|
We will have two cases,
1 = \frac{-3-4m}{4-3m} and 1 = -\frac{-3-4m}{4-3m}
4-3 = -3-4 and 4-3 = -(-3-4)
4m-3 = -3-4 and 4-3 = 3+4
m = -7 and 4+3 = 4-3
m = -7 and m = \frac{1}{7}
Hence, the equation of lines will be,
AB: (y-2) = m1(x-2)
y-2 = \frac{1}{7}(x-2)
7y-x-12=0
BC: (y-2) = m2(x-2)
y-2 = -7(x-2)
7x+y-16=0
Question 7: The equation of one side of an equilateral triangle is x-y=0 and one vertex is (2+√3,5). Prove that a second side is y+(2-√3)x=6 and find the equation of the third side.
Solution:
As equation of one side of equilateral triangle is x-y=0 and one vertex is (2+√3,5),
As, the point (2+√3,5) does not satisfy x-y=0. Then this is the vertex opposite of the line x-y=0

In equilateral triangle,
∠A = ∠B = ∠C = 60°
We can say that, AC and BC makes 60° with AB.
Let the slope of AC as m1 and BC as m2.
AB: (y-5) = m1(x-(2+√3))
BC: (y-5) = m2(x-(2+√3))
Slope of AC : x-y=0
y = x
Slope of AC is 1.
Here, it is given that these two lines make an angle of 60° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 60°, m = m1 and m2 and M = 1
tan 60° = |\frac{1-m}{1+m(1)}|
√3= |\frac{1-m}{1+m}|
We will have two cases,
√3 = \frac{1-m}{1+m} and √3 = -\frac{1-m}{1+m}
m = \frac{1-\sqrt{3}}{1+\sqrt{3}} and √3(1+m) = -(1-m)
m = \frac{1-\sqrt{3}}{1+\sqrt{3}} and √3+√3m = m-1
m = \frac{1-\sqrt{3}}{1+\sqrt{3}} and √3m-m = -1-√3
m = \frac{1-\sqrt{3}}{1+\sqrt{3}} and m = \frac{1+\sqrt{3}}{1-\sqrt{3}}
After rationalizing, we get
m = \frac{(1-\sqrt{3})^2}{1-3} and m = \frac{(1+\sqrt{3})^2}{1-3}
m = \frac{1+3-2\sqrt{3}}{-2} and m = \frac{1+3+2\sqrt{3}}{-2}
m = -(2-√3) and m = -(2+√3)
Hence, the equation of lines will be,
AB: (y-5) = m1(x-(2+√3))
y-5 = -(2-√3)(x-(2+√3))
y-5 = -(2-√3)x+ (22-(√3)2)
(2-√3)x+y-6 = 0
BC: (y-5) = m2(x-(2+√3))
(y-5) = -(2+√3)(x-(2+√3))
y-5 = -(2+√3)x+(2+√3)^2
(2+√3)x+y-5 = 4+3+4√3
(2+√3)x+y = 12+4√3
Question 8: Find the equation of the two straight lines passing through (1,2) forming two sides of a square of which 4x+7y=12 is one diagonal.
Solution:
Let the point opposite of diagonal 4x+7y=12 be C(1,2)
Here, △BCD form an isosceles right angled triangle at C.
∠B = ∠D = 45°
We can say that, CD and BC makes 45° with BD.
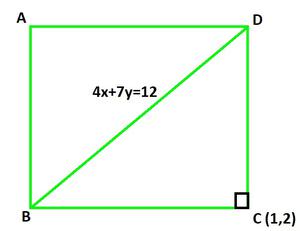
Let the slope of CD as m1 and BC as m2.
CD: (y-2) = m1(x-1)
BC: (y-2) = m2(x-1)
Slope of BD : 4x+7y=12
y = \frac{-4}{7}x + 3
Slope of BD is \frac{-4}{7}.
Here, it is given that these two lines make an angle of 45° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 45° and M = \frac{-4}{7}
tan 45° = |\frac{\frac{-4}{7}-m}{1+m(\frac{-4}{7})}|
1 = |\frac{\frac{-4-7m}{7}}{1-m(\frac{4}{7})}|\\ 1 = |\frac{\frac{-4-7m}{7}}{\frac{7-4m}{7}}|\\ 1 = |\frac{-4-7m}{7-4m}|
We will have two cases,
1 = \frac{-4-7m}{7-4m} and 1 = -\frac{-4-7m}{7-4m}
7-4m = -4-7m and 7-4m = -(-4-7m)
7m-4m = -4-7 and 7-4m = 4+7m
3m = -11 and 7m+4m = 7-4
m = \frac{-11}{3} and 11m = 3
m = \frac{-11}{3} and m = \frac{3}{11}
Hence, the equation of lines will be,
CD: (y-2) = m1(x-1)
y-2 = \frac{-11}{3}(x-1)
3y-6 = -11x+11
11x+3y-17=0
BC: (y-2) = m2(x-1)
y-2 = \frac{3}{11}(x-1)
11y-22 = 3x-3
3x-11y+19=0
Question 9: Find the equation of the two straight lines passing through (1,2) and making an angle of 60° with the line x+y=0. Find also the area of the triangle formed by the three lines.
Solution:
As equation of one side of equilateral triangle is x+y=0 and one vertex is (1,2),
As, the point (1,2) does not satisfy x+y=0. Then this is the vertex opposite of the line x+y=0
Hence, the lines make an equilateral triangle,
∠A = ∠B = ∠C = 60°
We can say that, AC and BC makes 60° with AB.

Let the slope of AC as m1 and BC as m2.
AB: (y-2) = m1(x-1)
BC: (y-2) = m2(x-1)
Slope of AC : x+y=0
y = -x
Slope of AC is -1.
Here, it is given that these two lines make an angle of 60° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 60° and M = -1
tan 60° = |\frac{-1-m}{1+m(-1)}|
√3= |\frac{-1-m}{1-m}|
We will have two cases,
√3 = \frac{-1-m}{1-m} and √3 = -\frac{-1-m}{1-m}
√3(1-m) = -1-m and √3(1-m) = 1+m
√3-√3m = -1-m and √3-√3m = m+1
√3m-m = √3+1 and +√3m+m = √3-1
m = \frac{\sqrt{3}+1}{\sqrt{3}-1} and m = \frac{\sqrt{3}-1}{\sqrt{3}+1}
After rationalizing, we get
m = \frac{(\sqrt{3}+1)^2}{3-1} and m = \frac{(\sqrt{3}-1)^2}{3-1}
m = \frac{1+3+2\sqrt{3}}{2} and m = \frac{1+3-2\sqrt{3}}{2}
m = 2+√3 and m = 2-√3
Hence, the equation of lines will be,
AB: (y-2) = (2+√3)(x-1)
y-2=(2+√3)x-2-√3
(2+√3)x-y-√3=0 ...................(i)
BC: (y-2) = (2-√3)(x-1)
y-2=(2-√3)x-2+√3
(2-√3)x-y+√3=0 ...................(ii)
Using (i) and x+y=0, we get
A = (\frac{-1-\sqrt{3}}{2},\frac{1+\sqrt{3}}{2})
C = (1,2)
Using distance formula, AC
AC = \sqrt{(1-\frac{-1-\sqrt{3}}{2})^2+(2-\frac{1+\sqrt{3}}{2})^2}\\ AC = \sqrt{(\frac{2+1+\sqrt{3}}{2})^2+(\frac{4-1-\sqrt{3}}{2})^2}\\ AC = \sqrt{(\frac{3+\sqrt{3}}{2})^2+(\frac{3-\sqrt{3}}{2})^2}\\ AC = \sqrt{\frac{9+3+6\sqrt{3}+9+3-6\sqrt{3}}{4}}\\ AC = \sqrt{\frac{24}{4}}\\ AC = \sqrt{6}
Area of equilateral triangle ABC,
= \frac{\sqrt{3}}{4}(side)^2\\ = \frac{\sqrt{3}}{4}(\sqrt{6})^2\\ = \frac{\sqrt{3}}{4}(6)\\ = \frac{3\sqrt{3}}{2} sq. unit
Question 10: Two sides of an isosceles triangle are given by the equations 7x-y+3=0 and x+y-3=0 and its third side passes through the point (1,-10). Determine the equation of the third side.
Solution:
Let the equation of the line AB and AC 7x-y+3=0 and x+y-3=0 respectively.
∠B = ∠C
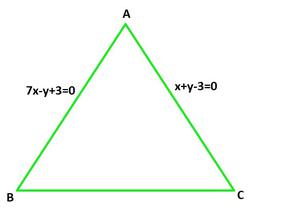
Slope of line AB: 7x-y+3=0
y = 7x+3
Slope m1 = 7
Slope of line AC: x+y-3=0
y = -x+3
Slope m2 = -1
Let the slope of line BC be m, which passes through the point (1,-10)
y-(-10) = m(x-1)
y+10 = m(x-1)
The angle between the lines AB and BC is equal to the angle between the lines AC and BC, say θ
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
By taking positive sign
tan θ = \frac{m-7}{1+7m} = \frac{m-(-1)}{1+m(-1)}
tan θ = \frac{m-7}{1+7m} = \frac{m+1}{1-m}
Solving it, we get
m = -3 or \frac{1}{3}
By taking negative sign
tan θ = \frac{m-7}{1+7m} = -\frac{m-(-1)}{1+m(-1)}
tan θ = \frac{m-7}{1+7m} = -\frac{m+1}{1-m}
Solving it, we get
m2 = -1 (which is not possible)
Line BC: when m = -3
y+10 = -3(x-1)
y+10 = -3x+3
3x+y-13=0
Line BC: when m = \frac{1}{3}
y+10 = \frac{1}{3}(x-1)
3y+30 = x-1
x-3y-31=0
Question 11: Show that the point (3,-5) lies between the parallel lines 2x+3y-7=0 and 2x+3y+12=0 and find the equation of lines through (3,-5) cutting the above lines at an angle of 45°.
Solution:
Let the line 1: 2x+3y-7=0
Line 2: 2x+3y+12=0
As the slope of line 1 and line 2 is same, these lines are parallel.
Slope of lines M = \frac{-2}{3}
To check whether (3,-5) lies between these lines
Taking x=3 and y=-5
(2x+3y-7)(2x+3y+12)<0 (If its true then the point lies between these lines)
(2(3)+3(-5)-7)(2(3)+3(-5)+12)
(6-15-7)(6-15+12)
(-16)(3) <0, which is a negative value.
Hence, the point (3,-5) lies between the lines.

Let the slope of the line be m, which is passing through the point (3,-5)
y-(-5) = m(x-3)
y+5 = m(x-3)
As it is given that the line is cutting above lines at an angle of 45°.
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Taking θ = 45° and M = \frac{-2}{3}
By taking positive sign
tan 45° = |\frac{\frac{-2}{3}-m}{1+m(\frac{-2}{3})}|
1 = |\frac{\frac{-2-3m}{3}}{1-m(\frac{2}{3})}|
1 = |\frac{\frac{-2-3m}{3}}{\frac{3-2m}{3}}|
1 = |\frac{-2-3m}{3-2m}|
We will have two cases,
1 = \frac{-2-3m}{3-2m} and 1 = -\frac{-2-3m}{3-2m}
3-2m = -2-3m and 3-2m = -(-2-3m)
3m-2m = -2-3 and 3-2m = 2+3m
m = -5 and 3m+2m = 3-2
m = -5 and m = \frac{1}{5}
Hence, the equation of line will be,
when m = -5
y+5 = (-5)(x-3)
y+5 = -5x+15
5x+y-10=0
when m = \frac{1}{5}
y+5 = \frac{1}{5} (x-3)
5y+25 = x-3
x-5y-28=0
Question 12: The equation of the base of an equilateral triangle is x+y=2 and its vertex is (2,-1). Find the length and equations of its sides.
Solution:
∠A = ∠B = ∠C = 60°
We can say that, AC and AB makes 60° with BC.
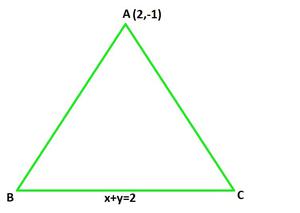
Let the slope of AC as m1 and AB as m2 which passes through the point (2,-1).
AB: (y-(-1)) = m1(x-2)
y+1 = m1(x-2)
AC: (y-(-1)) = m2(x-2)
y+1 = m2(x-2)
Slope of BC : x+y=2
y = -x+2
Slope of BC is -1.
Here, it is given that these two lines make an angle of 60° between them. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 60°, m = m1 and m2 and M = -1
tan 60° = |\frac{-1-m}{1+m(-1)}|
√3= |\frac{-1-m}{1-m}|
We will have two cases,
√3 = \frac{-1-m}{1-m} and √3 = -\frac{-1-m}{1-m}
√3(1-m) = -1-m and √3(1-m) = 1+m
√3-√3m = -1-m and √3-√3m = m+1
√3m-m = √3+1 and +√3m+m = √3-1
m = \frac{\sqrt{3}+1}{\sqrt{3}-1} and m = \frac{\sqrt{3}-1}{\sqrt{3}+1}
After rationalizing, we get
m = \frac{(\sqrt{3}+1)^2}{3-1} and m = \frac{(\sqrt{3}-1)^2}{3-1}
m = \frac{1+3+2\sqrt{3}}{2} and m = \frac{1+3-2\sqrt{3}}{2}
m = 2+√3 and m = 2-√3
Hence, the equation of lines will be,
AB: y+1 = m1(x-2)
y+1 = (2+√3)(x-2)
y+1 = (2+√3)x-4-2√3
(2+√3)x-y-5-2√3=0 ...................(i)
AC: y+1 = m2(x-2)
y+1 = (2-√3)(x-2)
y+1 = (2-√3)x-4+2√3
(2-√3)x-y-5+2√3=0 ...................(ii)
Using (ii) and x+y=2, we get
C = (\frac{15+\sqrt{3}}{6},-\frac{3+\sqrt{3}}{6})
A = (2,-1)
Using distance formula, AC
AC = \sqrt{(2-\frac{15+\sqrt{3}}{6})^2+(-1-(-\frac{3+\sqrt{3}}{6}))^2}\\ AC = \sqrt{(\frac{12-15-\sqrt{3}}{6})^2+(\frac{-6+3+\sqrt{3}}{6})^2}\\ AC = \sqrt{(\frac{-3-\sqrt{3}}{6})^2+(\frac{-3+\sqrt{3}}{6})^2}\\ AC = \sqrt{\frac{9+3+6\sqrt{3}+9+3-6\sqrt{3}}{36}}\\ AC = \sqrt{\frac{24}{36}}\\ AC = \sqrt{\frac{2}{3}}
AC = AB = BC = \sqrt{\frac{2}{3}}
Question 13: If two opposite vertices of a square are (1,2) and (5,8), find the coordinates of its other two vertices and the equations of its sides.
Solution:
Let's consider a square ABCD.
According to the property of square, the diagonal bisects the angle.
Hence, ∠AOB = ∠AOD = 45°

Slope of the diagonal AC:
\frac{8-2}{5-1} = \frac{6}{4} = \frac{3}{2}
Let the slope of the line AB and AD be m1 and m2, which passes through the point (1,2)
AB: y-2 = m1(x-1)
AD: y-2 = m2(x-1)
Here, it is given that these two lines make an angle of 45° with AC. Hence,
As we know that, two lines having slopes as m and M will have angle θ between them as follows:
\mathbf{tan θ = |\frac{M-m}{1+mM}|}
Here, we have θ = 45°, m = m1 and m2 and M = \frac{3}{2}
tan 45° = |\frac{\frac{3}{2}-m}{1+m(\frac{3}{2})}|
1 = |\frac{\frac{3-2m}{2}}{\frac{2+3m}{2}}|
1= |\frac{3-2m}{2+3m}|
We will have two cases,
1 = \frac{3-2m}{2+3m} and 1 = -\frac{3-2m}{2+3m}
2+3m = 3-2m and 2+3m = -(3-2m)
3m+2m = 3-2 and 2+3m = 2m-3
5m = 1 and 3m-2m = -3-2
m = \frac{1}{5} and m = -5
m = \frac{1}{5} or -5
Hence, the equation of lines will be,
AB: y-2 = m1(x-1)
y-2 = \frac{1}{5}(x-1)
5y-10 = x-1
x-5y+9=0 ...................(i)
AD: y-2 = m2(x-1)
y-2 = -5(x-1)
y-2 = -5x+5
5x+y-7=0 ...................(ii)
As BC is parallel to AD, So
The equation BC will be 5x+y+λ=0 and as BC passes through C(5,8), we get
5(5)+(8)+λ=0
33+λ=0
λ = -33
Hence, Equation of BC is 5x+y-33=0 ...................(iii)
Now as CD is parallel to AB, So
The equation CD will be x-5y+λ=0 and as CD passes through C(5,8), we get
5-5(8)+λ=0
-35+λ=0
λ = 35
Hence, Equation of CD is x-5y+35=0 ...........................(iv)
Solving (i) and (iii), we get
B(6,3)
Solving (ii) and (iv), we get
D(0,7)
Hence, the equation of lines are
AB = x-5y+9=0
BC = 5x+y-33=0
CD = x-5y+35=0
AD = 5x+y-7=0
And the vertices of square are
A(1,2), B(6,3), C(5,8) and D(6,3)
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice