Class 11 RD Sharma Solutions - Chapter 6 Graphs of Trigonometric Functions - Exercise 6.3

Last Updated : 08 May, 2021

Sketch the graphs of the following functions:

Question 1: y = sin² x

Solution:

As we know that,

y = sin² x = \frac{1- cos 2x}{2} = \frac{1}{2} - \frac{cos 2x}{2}

y - \frac{1}{2} = -\frac{cos 2x}{2}

On shifting the origin at (0, 1/2), we get

X = x and Y = y – \frac{1}{2}

On substituting these values, we get

Y = - \frac{cos 2X}{2}

The maximum and minimum values of Y are \frac{1}{2} and -\frac{1}{2} respectively and shift it by 1/2 to the up.

As the equation in the form of y = - f(x), the graph become inverted of y = f(x)

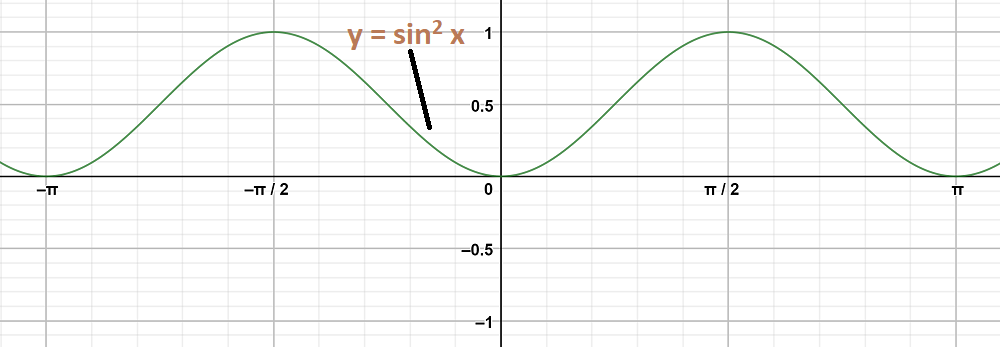
Question 2: y = cos² x

Solution:

As we know that,

y = cos² x = \frac{1+ cos 2x}{2} = \frac{1}{2} + \frac{cos 2x}{2}

y - \frac{1}{2} = \frac{cos 2x}{2}

On shifting the origin at (0, \frac{1}{2}) , we get

X = x and Y = y – \frac{1}{2}

On substituting these values, we get

Y = \frac{cos 2X}{2}

The maximum and minimum values of Y are \frac{1}{2} and -\frac{1}{2} respectively and shift it by 1/2 to the up.

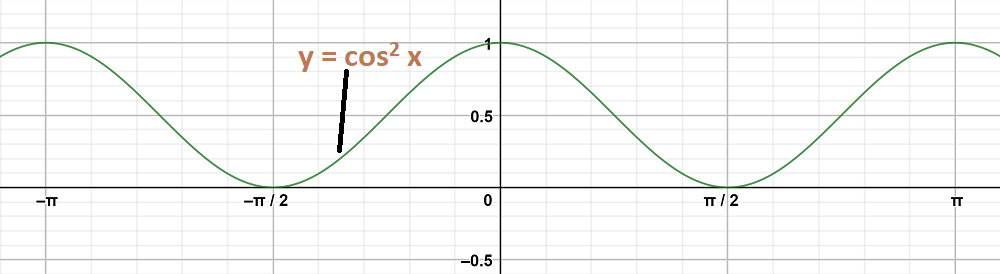
Question 3: y = sin² (x-\frac{\pi}{4})

Solution:

To obtain this graph y-0 = sin² (x-\frac{\pi}{4})

On shifting the origin at (\frac{\pi}{4} ,0), we get

X = x-\frac{\pi}{4} and Y = y – 0

On substituting these values, we get

Y = sin² X

First we draw the graph of Y = sin² X and shift it by π/4 to the right.

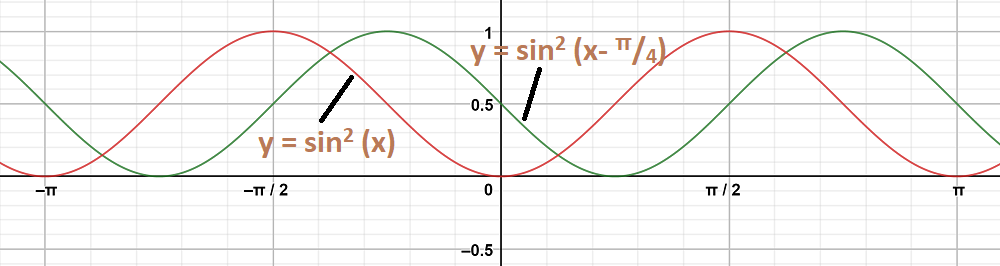
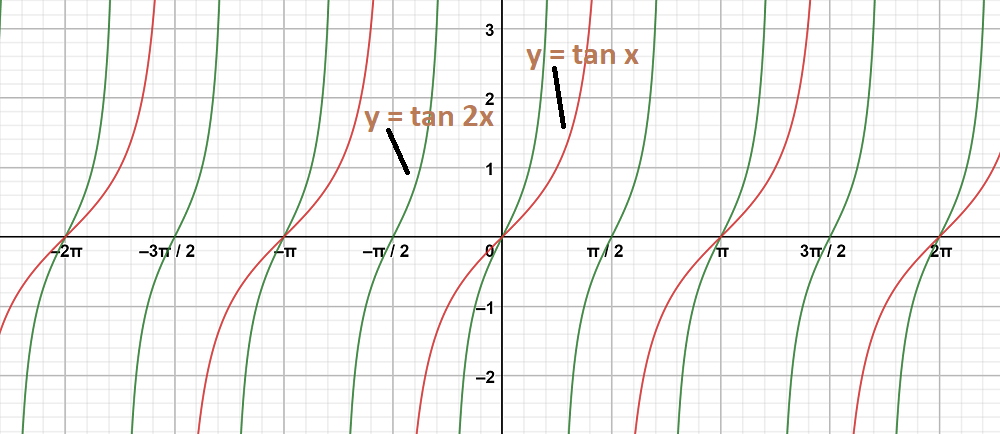
Question 4: y = tan 2x

Solution:

To obtain this graph y = tan 2x,

First we draw the graph of y = tan x and then divide the x-coordinates of the points where it crosses x-axis by 2.

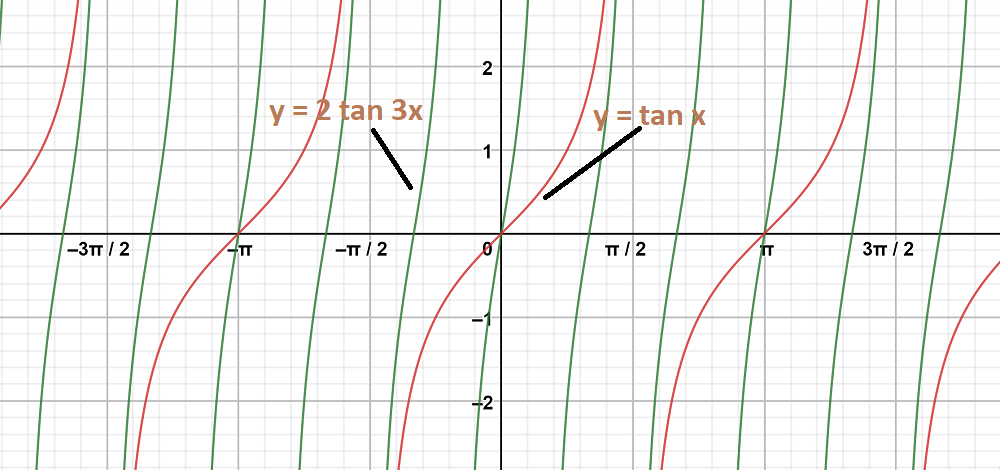
Question 5: y = 2 tan 3x

Solution:

To obtain this graph y = 2 tan 3x,

First we draw the graph of y = tan x and then divide the x-coordinates of the points where it crosses x-axis by 3.

Stretch the graph vertically by the factor of 2.

Question 6: y = 2 cot 2x

Solution:

To obtain this graph y = 2 cot 2x,

First we draw the graph of y = cot x and then divide the x-coordinates of the points where it crosses x-axis by 2.

Stretch the graph vertically by the factor of 2.

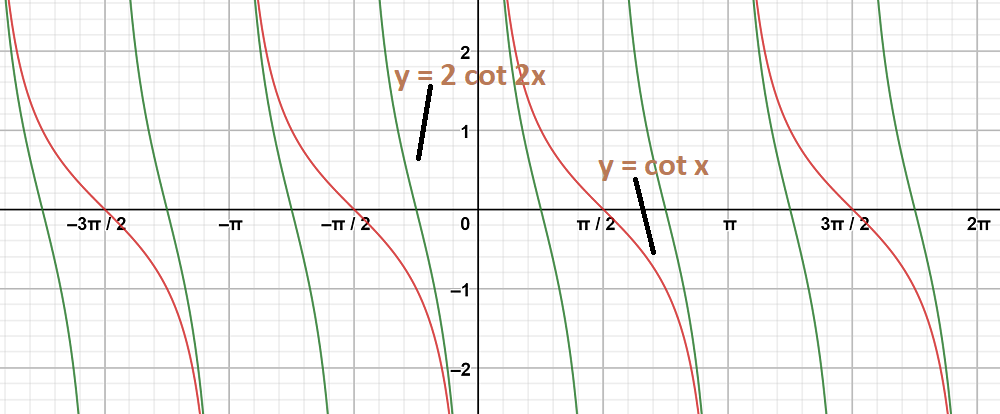
Sketch the graphs of the following functions on the same scale:

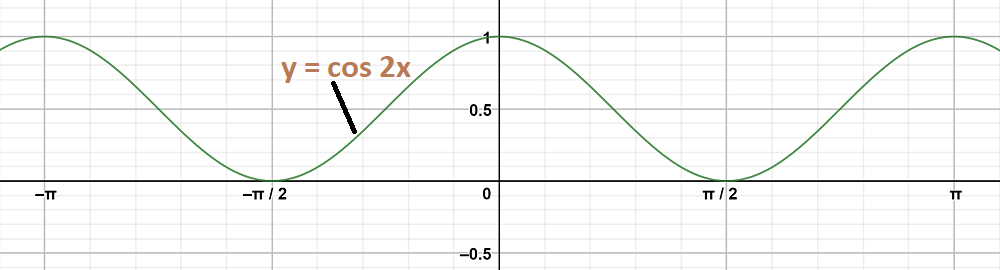
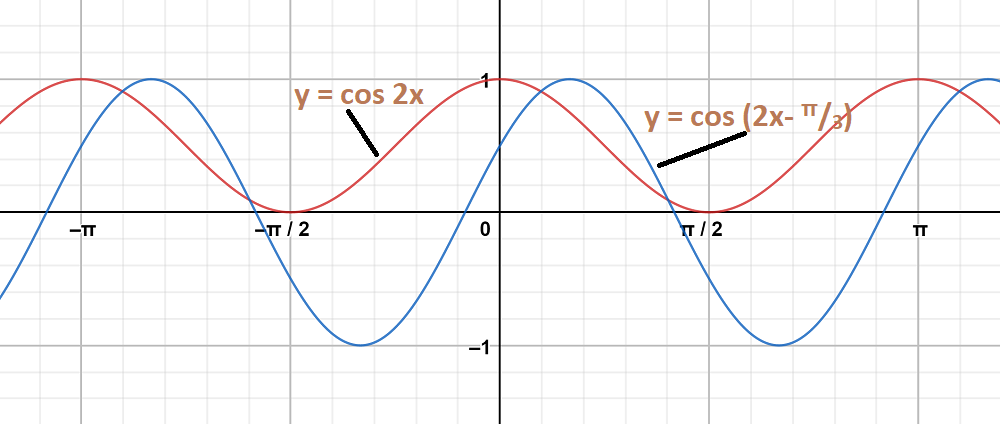
Question 7: y = cos ²x, y = cos (2x-\frac{\pi}{3})

Solution:

Graph 1:

y = cos² x

As we know that,

y = cos² x = \frac{1+ cos 2x}{2} = \frac{1}{2} + \frac{cos 2x}{2}

y - \frac{1}{2} = \frac{cos 2x}{2}

On shifting the origin at (0, 1/2), we get

X = x and Y = y – \frac{1}{2}

On substituting these values, we get

Y = \frac{cos 2X}{2}

The maximum and minimum values of Y are \frac{1}{2}  and -\frac{1}{2}  respectively and shift it by 1/2 to the up.

Graph 2:

To obtain this graph y-0 = cos (2x-\frac{\pi}{3} ) = cos 2(x-\frac{\pi}{6} )

On shifting the origin at (π/6, 0), we get

X = x-\frac{\pi}{6}  and Y = y - 0

On substituting these values, we get

Y = cos 2X

First we draw the graph of Y = cos 2X and shift it by π/6 to the right.

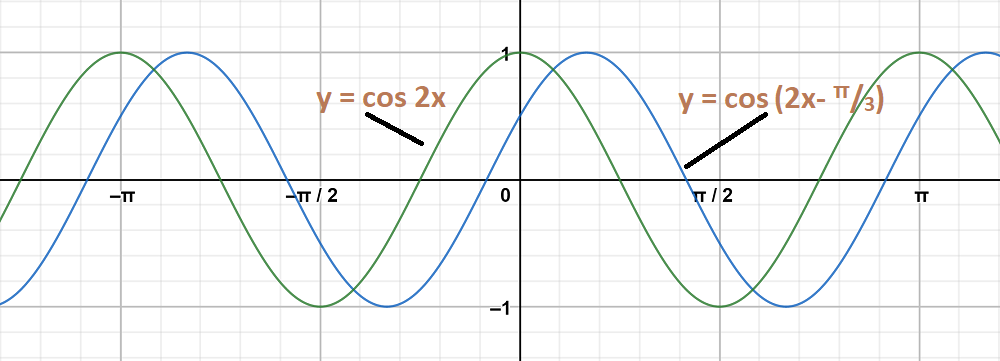
The graph y = cos² x and y = cos (2x-\frac{\pi}{3})  are on same axes are as follows:

Question 8: y = sin² x, y = sin x

Solution:

Graph 1:

y = sin² x

As we know that,

y = sin² x = \frac{1- cos 2x}{2} = \frac{1}{2} - \frac{cos 2x}{2}

y - \frac{1}{2} = -\frac{cos 2x}{2}

On shifting the origin at (0, \frac{1}{2} ), we get

X = x and Y = y – \frac{1}{2}

On substituting these values, we get

Y = - \frac{cos 2X}{2}

The maximum and minimum values of Y are \frac{1}{2} and -\frac{1}{2} respectively and shift it by 1/2 to the up.

As the equation in the form of y = - f(x), the graph become inverted of y = f(x)

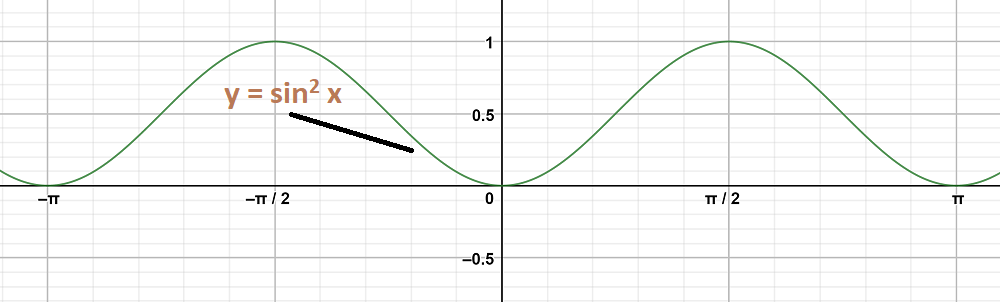
Graph 2:

y = sin x

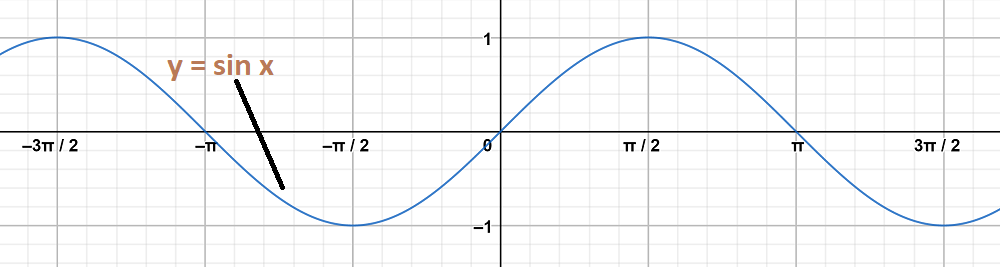
The graph y = sin² x and y = sin x are on same axes are as follows:

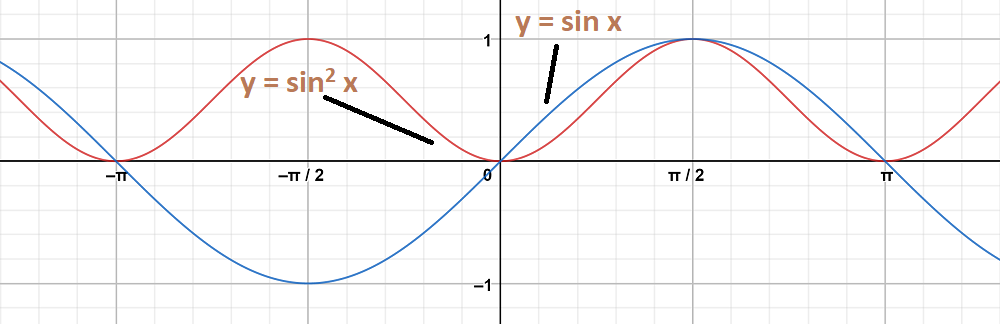
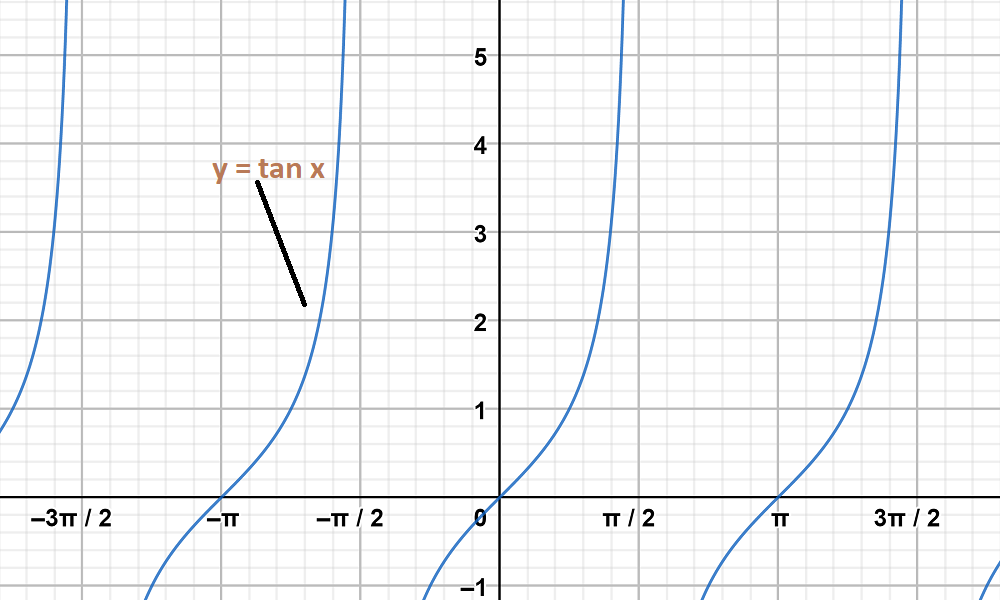
Question 9: y = tan x, y = tan ²x

Solution:

Graph 1:

y = tan x

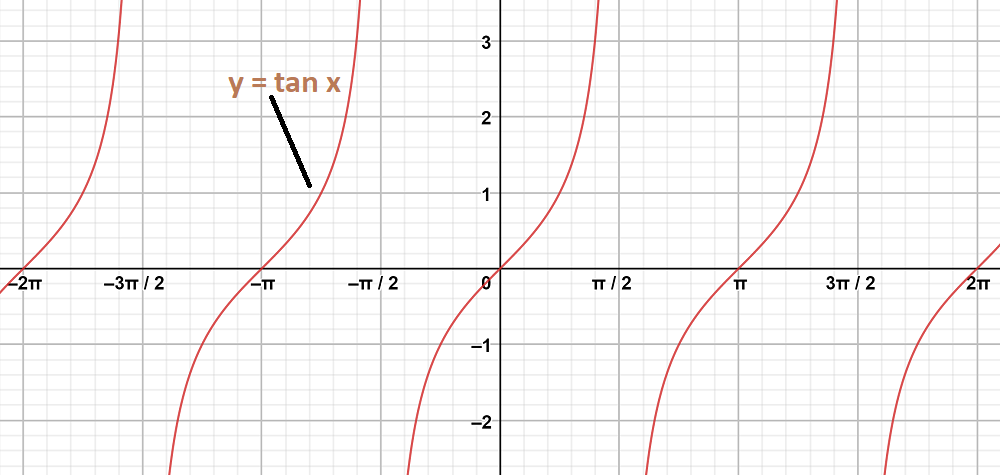
Graph 2:

y = tan² x

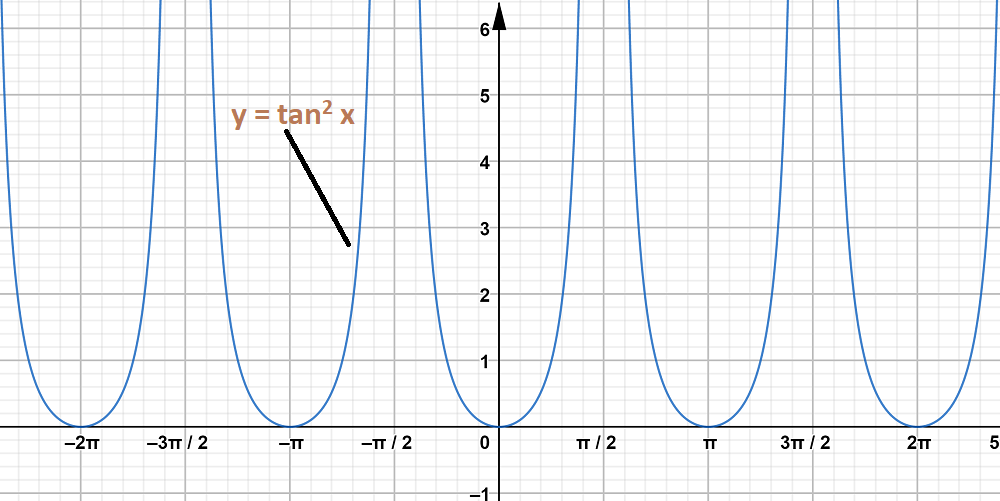
The graph y = tan x and y = tan² x are on same axes are as follows:

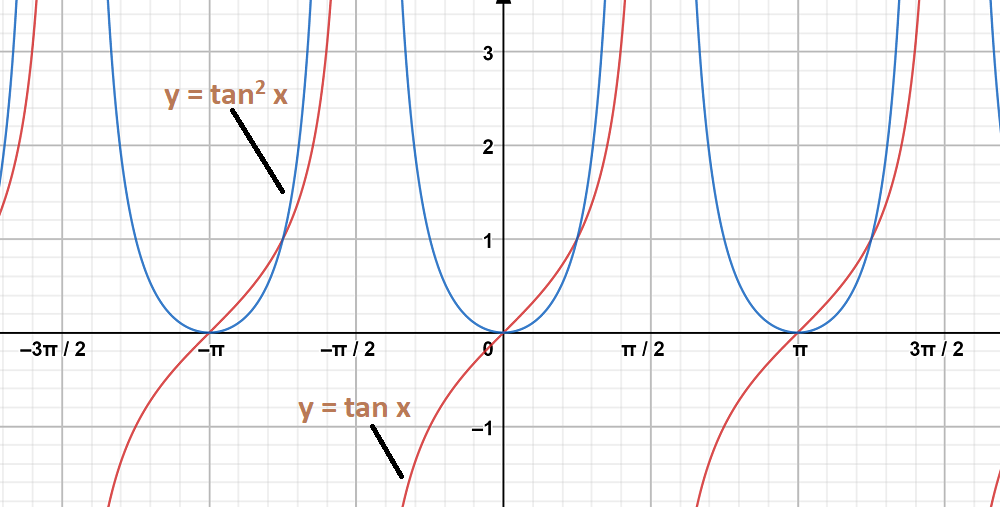
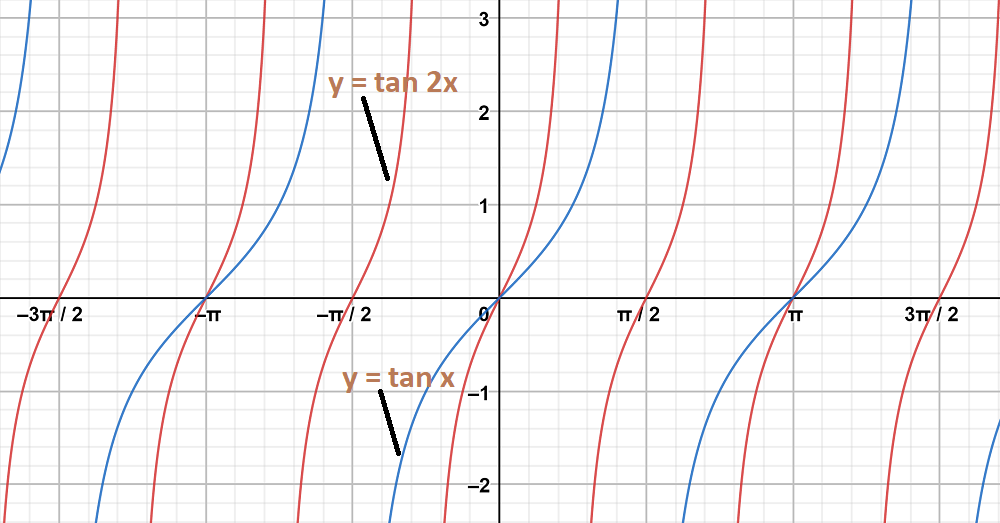
Question 10: y = tan 2x, y = tan x

Solution:

Graph 1:

To obtain this graph y = tan 2x,

First we draw the graph of y = tan x and then divide the x-coordinates of the points where it crosses x-axis by 2.

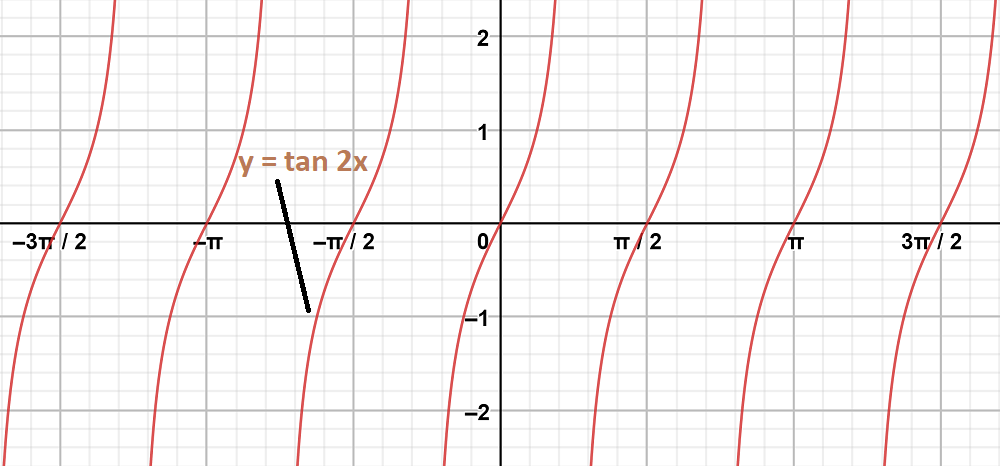
Graph 2:

y = tan x

The graph y = tan 2x and y = tan x are on same axes are as follows: