Class 12 RD Sharma Solutions - Chapter 21 Areas of Bounded Regions - Exercise 21.1 | Set 2

In Chapter 21 of Class 12 RD Sharma, "Areas of Bounded Regions" we delve into the fundamental concepts of finding areas under curves and bounded regions using the integration. This chapter builds on the understanding of the definite integrals and their application in determining the area between the two curves. The exercise is aimed at strengthening students' problem-solving skills by applying these concepts to the various problems involving bounded regions.

Areas of Bounded Regions

The concept of areas of bounded regions involves calculating the area between the curves which is an essential topic in calculus. By integrating the difference between the functions representing the curves over a given interval students can determine the area enclosed by these curves. This technique is particularly useful in scenarios where the curves intersect forming a closed region whose area can be computed using the definite integrals.

Question 11. Sketch the region {(x, y): 9x² + 4y² = 36} and find the area enclosed by it, using integration.

Solution:

9x2 + 4y2 = 36

\frac{x^2}{4}+\frac{y^2}{9}=1\\ y=\pm\sqrt{\frac{36-9x^2}{4}}

Area of Sector OABCO = \displaystyle \int_0^2\sqrt{\frac{36-9x^2}{4}}\ dx\\ =\frac{3}{2}\int_0^2\sqrt{4-x^2}\ dx\\ =\frac{3}{2}\left[\frac{x\sqrt{4-x^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{x}{2}\right)\right]_0^2\\ =\frac{3}{2}\left[\frac{2\sqrt{4-2^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{2}{2}\right)\right]-\frac{3}{2}\left[\frac{0\sqrt{4-0^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{0}{2}\right)\right]\\ =\frac{3}{2}\times2\times\frac{\pi}{2}-0\\ =\frac{3\pi}{2}\ sq.\ units

Area of the whole figure = 4 x area of DOABCO

=4\times\frac{3\pi}{2}\\ =6\pi\ sq.\ units.

Question 12. Draw a rough sketch of the graph of the function y=2\sqrt{1-x^2} , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis

Solution:

Here, we have to find the area enclosed between the curve and x-axis.

y=2\sqrt{1-x^2},\ x\ ∈\ [0,\ 1 ]\\ \Rightarrow y^2+4x^2=4,\ x\ ∈\ [0,\ 1]\\ \Rightarrow \frac{x^2}{1}+\frac{y^2}{4},\ x\ ∈\ [0,\ 1]

Equation (1) represents an ellipse with centre at origin and passes through (±1, 0) and (0, ±2) and x ∈ [0, 1] as represented by region between y-axis and line x = 1.

Here, is the rough sketch.

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = 1,

Thus,

Required area = Region OAPBO

\displaystyle =\int_0^1y\ dx\\ =\int_0^12\sqrt{1-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(x)\right]_0^1\\ =2\left[\left(\frac{1}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =2\left[0+\frac{1}{2}\times\frac{\pi}{2}\right]

Required area = \frac{\pi}{2}   square units

Question 13. Determine the area under the curve y=\sqrt{a^2-x^2}  included between the line x = 0 and x = 8.

Solution:

Here,

We have to find area under the curve

y =\sqrt{a^2-x^2}

x2 + y2 = a  ...........(1)

between x = 0    .........(2)

x = a    ...........(3)

Equation (1) represents a circle with Centre (0, 0) and passes axes at (0, ±a), (±a, 0).

Equation (2) represents y-axis and 

Equation x = a represents  a line parallel to y-axis passing through (a, 0)

Here, is the rough sketch,

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = a,

Thus,

Required area = Region OAPBO

\displaystyle =\int_0^ay\ dx\\ =\int_0^a\sqrt{a^2-x^2}\ dx\\ =\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0)\right]\\ =2\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]

Required area = \frac{\pi}{4}a^2   square units

Question 14. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8

Solution:

Here,

We have to find area bounded by x-axis

2y + 5x = 7   .........(1)

x = 2      ........(2)

x = 8    .........(3)

Equation (1)  represents line passing through \left(-\frac{7}{5},\ 0\right)   and \left(0,\ \frac{7}{2}\right)   equation.

Equation (2), (3) shows line parallel to y-axis passing through (2, 0), (8, 0) respectively.

Here, is the rough sketch;

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 2 to x = 8,

Thus,

Required area = Region ABCDA

\displaystyle =\int_2^8\left(\frac{5x+7}{2}\right)\\ =\frac{1}{2}\left(\frac{5x^2}{2}+7x\right)_2^8\\ =\frac{1}{2}\left[\left(\frac{5(8)^2}{2}+7(8)\right)-\left(\frac{5(2)^2}{2}+7(2)\right)\right]\\ =\frac{1}{2}[(160+56)-(10+14)]\\ =\frac{192}{2}

Required area = 96 square units

Question 15. Using definite integrals, find the area of the circle x² + y² = a²

Solution:

Here, we have to find the area of circle,

x2 + y2 = a2

Equation (1) represents a circle with centre (0, 0) and radius a, Thus is meets the axes (±a, 0), (0, ±a).

Here, is the rough sketch;

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = a,

Thus,

Required area = Region ABCDA

= 4 ( Region ABOA)

\displaystyle =4\int_0^ay\ dx\\ =4\int_0^a\sqrt{a^2-x^2}\ dx\\ =4\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =4\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =4\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]\\ =4\left(\frac{a^2\pi}{4}\right)

Question 16. Using the integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = -2, x = 3, y = 

Solution:

Here, we have to find the area enclosed by;

x = -2,

x = 3,

y = 0 and

y = 1 + |x + 1|

⇒ y = 1 + x + 1, if x + 1 0

⇒ y = 2 + x    ..........(1), if x ≥ -1

and

⇒ y = 1 - (x + 1), if x + 1 < 0

⇒ y = 1 - x - 1, if x < -1

⇒ y = -x    .........(2), if x < -1

Thus,

Equation (1) is a straight line that passes through (0, 2) and (-1 , 1).

Equation (2) is a line passing through (-1, 1) and (-2, 2) and it is enclosed by line x = 2 and x = 3 which are lines parallel to y-axis and pass through (2, 0) and (3, 0) respectively y = 0 is x-axis 

Here is the rough sketch

Shaded region represents the required area.

Thus,

Required area = Region (ABECDFA)

Required area = (Region ABEFA + Region ECDFE)    ........(1)

Region ECDFE

We slice it into approximation rectangle of 

Width = △x

Length = y1

Area of rectangle = y1△x

The approx rectangles slide from x = -2 to x = -1,

Region ABEFA

We slice it into approximation rectangle of 

Width = △x

Length = y2

Area of rectangle = y2△x

The approx rectangles slide from x = -1 to x = 3,

Required area = \displaystyle \int_{-2}^{-1}y_1\ dx+\int_{-1}^3y_2\ dx\\ =-\left[\frac{x^2}{2}\right]^{-1}_{-2}+\left[\frac{x^2}{2}+2x\right]_{-1}^3\\ =-\left[\frac{1}{2}+\frac{4}{2}\right]+\left[\left(\frac{9}{2}+6\right)-\left(\frac{1}{2}-2\right)\right]\\ =\frac{3}{2}+\left(\frac{21}{2}+\frac{3}{2}\right)\\ =\frac{27}{2}

Required area = \frac{27}{2}   square units

Question 17. Sketch the graph y = |x -5|. Evaluate \displaystyle \int_0^1|x-5|\ dx . What does the value of the integral represent on the graph?

Solution:

Here, is the sketch of the given graph: 

y = |x - 5|

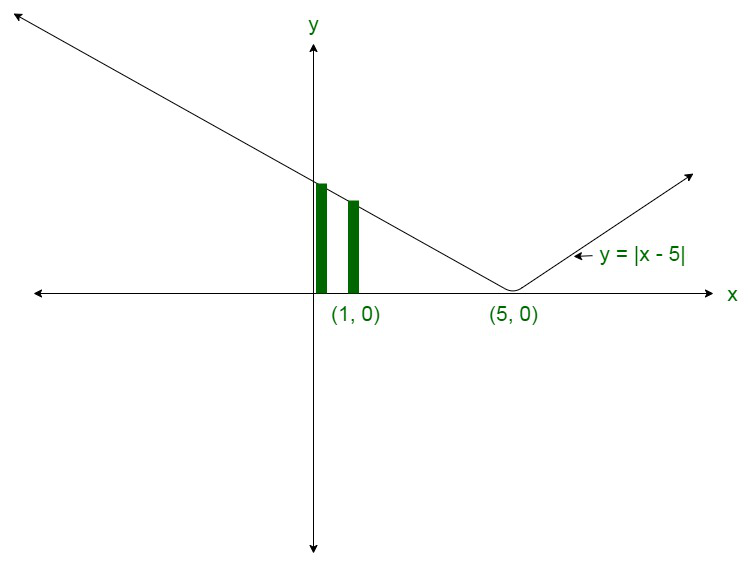
Hence,

Required area = \displaystyle =\int_0^1y\ dx\\ =\int_0^1|x-5|\ dx\\ =\int_0^1-(x-5)\ dx\\ =\left[\frac{-x^2}{2}+5x\right]_0^1\\ =\left[-\frac{1}{2}+5\right]\\ =\frac{9}{2}\ sq.\ units

Thus, 

The given integral represents the area bounded by the curves that are,

x = 0,

y = 0,

x = 1

and

y = -(x - 5).

Question 18. Sketch the graph of y = |x + 3| and evaluate \displaystyle \int_{-6}^0|x+3|\ dx. What does this integral represents on the graph?

Solution:

Here,

The given equation is y = |x + 3|

The corresponding values of x and y are given in the following table.

x	-6	-5	-4	-3	-2	-1	0
y	3	2	1	0	1	2	3

Thus, 

After plotting these points,

We will get the graph of y = |x + 3|

It is shown as;

It is known that (x + 3) ≤ 0 for -6 ≤ x ≤  -3 and (x + 3) ≥ 0 for -3 ≤ x ≤ 0

Therefore,

\displaystyle \int_{-6}^0|(x+3)|\ dx=-\int_{-6}^{-3}(x + 3)\ dx\\ =-\left[\frac{x^2}{2}+3x\right]_{-6}^{-3}+\left[\frac{x^2}{2}+3x\right]_{-3}^0\\ =\left[\left(\frac{(-3)^2}{2}+3(-3)\right)-\left(\frac{(-6)^2}{2}+3(-6)\right)\right]+\left[0-\frac{(-3)^2}{2}+3(-3)\right]\\ =-\left[-\frac{9}{2}\right]-\left[-\frac{9}{2}\right]\\ =9

Question 19. Sketch the graph y = |x + 1|. Evaluate \displaystyle \int_{4}^2|(x+1)|\ dx. What does the value of this integral represent on this graph?

Solution:

Here,

Given:

y = |x + 1|=\begin{cases} x+1,\ if\ x+1≥0\\ -(x+1),\ if\ x+1<0 \end{cases}\\ y=\begin{cases} (x+1),\ if\ x≥-1\\ -x-1,\ if\ x<-1 \end{cases}

y = x + 1   ............(1)

and

y = -x - 1   ..........(2)

Equation (1) represents a line which meets axes at (0, 1).

Equation (2) represents a line passing through (0, -1) and (-1, 0)

Here is the rough sketch

\displaystyle \int_{4}^2|(x+1)|\ dx=-\int_{-4}^{-1}(x + 1)\ dx\ +\int_{-1}^2(x+1)\ dx\\ =-\left[\frac{x^2}{2}+x\right]_{-4}^{-1}+\left[\frac{x^2}{2}+x\right]_{-1}^2\\ =-\left[\left(\frac{1}{2}-1\right)-\left(\frac{16}{2}-4\right)\right]+\left[\left(\frac{4}{2}+2\right)-\left(\frac{1}{2}-1\right)\right]\\ =-\left[\left(-\frac{1}{2}-4\right)\right]+\left[4+\frac{1}{2}\right]\\ =\frac{9}{2}+\frac{9}{2}\\ =\frac{18}{2}

Required area = 9 square units.

Question 20. Find the area of the region bounded by the curve xy - 3x - 2y - 10 = 0, x-axis and the lines x = 3, x = 4.

Solution:

Here,

We have to find the area bounded by

x axis,

x = 3,

x = 4

and

xy - 3x -2y - 10 = 0

⇒ y(x - 2) = 3x + 10

⇒ y=\frac{3x+10}{x-2}

Here, is the rough sketch

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 3 to x = 4,

Required area = Region ABCDA

\displaystyle =\int_3^4y\ dx\\ =\int_3^4\left(\frac{3x+10}{x-2}\right)\ dx\\ =\int_3^4\left(3+\frac{16}{x-2}\right)\ dx\\ =(3x)_3^4+16(log|x-2|)_3^4\\ =(12-9)+16(log2-log1)

Required area = (3 + 16 log2) square units.

Read More:

• Calculating the Volume of a Solid by Rotating Bounded Regions around the X-Axis
• Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.3

Summary

Chapter 21 of RD Sharma's Class 12 mathematics textbook focuses on Areas of Bounded Regions. Exercise 21.1 | Set 2 specifically deals with finding areas bounded by various curves and lines. Key points covered in this exercise set include:

• Calculating areas under curves using definite integrals
• Finding areas bounded by curves and coordinate axes
• Determining areas between two curves
• Handling different types of functions (polynomial, trigonometric, exponential, logarithmic)
• Applying symmetry to simplify area calculations
• Identifying appropriate limits of integration
• Interpreting the geometric meaning of integrals in area problems
• Dealing with absolute value functions in area calculations

This exercise set builds on the concepts introduced in Set 1 and provides more challenging problems to deepen students' understanding of area calculations using integration.