Class 12 RD Sharma Solutions - Chapter 21 Areas of Bounded Regions - Exercise 21.1 | Set 3

In this article, we will explore the solutions to Exercise 21.1 Set 3 from Chapter 21 of RD Sharma's Class 12 Mathematics textbook which focuses on "Areas of Bounded Regions". This chapter is crucial for students as it lays the foundation for understanding how to calculate the area under curves a key concept in integral calculus. The solutions provided here will guide students through the step-by-step process of solving problems related to bounded regions ensuring a strong grasp of the concepts involved.

Areas of Bounded Regions

The area of bounded regions refers to the space enclosed between two or more curves or a curve and a line within a given interval. This area is typically found by integrating the difference between the functions defining the curves over the specified interval. Understanding this concept is essential for solving problems in integral calculus and finding areas under curves.

Question 21. Draw a rough sketch of the curve y=\frac{π}{2}+2sin^2x  and find the area between x-axis, the curve, and the ordinates x = 0, x = π

Solution:

Here, we have to find the bounded by 

y=\frac{\pi}{2}+2sin^2x

x-axis, x = 0 and x = π

Here is the table for values of y=\frac{\pi}{2}+2sin^2x

x	0	\frac{\pi}{6}	\frac{\pi}{4}                           \frac{\pi}{3}	\frac{\pi}{2}	\frac{2\pi}{3}                      \frac{3\pi}{4}	\frac{5\pi}{6}	π
\frac{\pi}{2}+2\ sin^2x	1.57	2.07	2.57                  3.07	3.57	3.07            2.57	2.07	1.57

Here is the rough sketch,

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = π,

Thus,

Required area = Region ABCDO

\displaystyle =\int_0^π y\ dx\\ =\int_0^π\left(\frac{π}{2}+2sin^2x\right)\ dx\\ =\int_0^π\left(\frac{π}{2}+1-cos\ 2x\right)\ dx\\ =\left[\frac{π}{2}x+x-\frac{sin\ 2x}{2}\right]_0^π\\ =\left[\left(\frac{π^2}{2}+π-\frac{sin\ 2x}{2}\right)-(0)\right]\\ =\frac{π^2}{2}+π

Required area = \frac{π}{2}(π+2)      square units

Question 22. Draw a rough sketch of the curve y=\frac{x}{π}+2sin^2x  and find the area between the x-axis, the curve and the ordinates x = 0, x = π.

Solution:

Here, we have the area between y-axis,

x = 0,

x = π

and

y=\frac{x}{π}+2\ sin^2x\ \ \ \ \ ......(1)

Thus, the table for equation (1) is

x	0      \frac{π}{6}	\frac{π}{4}	\frac{π}{3}	\frac{π}{2}\ \ \ \ \frac{2π}{3}\ \ \ \ \ \frac{3π}{4}\ \ \ \ \ \frac{5π}{6}	π
y	0         0.66	1.25	1.88	2.5  1.88   1.25   0.66	0

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = π,

Thus,

Required area = Region ABOA

\displaystyle =\int_0^π y\ dx\\ =\int_0^π\left(\frac{π}{2}+2sin^2x\right)\ dx\\ =\int_0^π\left(\frac{π}{2}+1-cos\ 2x\right)\ dx\\ =\left[\frac{π}{2x}x+x-\frac{sin\ 2x}{2}\right]_0^π\\ =\left[\left(\frac{π^2}{2x}+π-0\right)-(0)\right]\\

Required area = \frac{3\pi}{2} square units

Question 23. Find the area bounded by the curve y = cos x between x = 0 and x = 2π

Solution:

Here from the figure we can see that

The required area = area of the region OABO + area of the region BCDB + area of the region DEFD

Therefore,

The required area = \displaystyle \int_0^{\frac{\pi}{2}}cos\ x\ dx+\left|\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}}cos\ x\ dx\right|+\int_{\frac{3\pi}{2}}^{2\pi}cos\ x\ dx\\ =[sin\ x]_0^{\frac{\pi}{2}}+\left|[sin\ x]^{\frac{3\pi}{2}}_{\frac{\pi}{2}}\right|+[sin\ x]^{2\pi}_{\frac{3\pi}{2}}\\ =\left[sin\frac{\pi}{2}-sin0\right]+\left|sin\frac{3\pi}{2}-sin\frac{\pi}{2}\right|+\left[sin\ 2x-sin\frac{3\pi}{2}\right]\\ =1+2+1\\ =4\ sq.\ units

Question 24. Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x = \frac{π}{3}  are the ratio 2:3.

Solution:

We have to find the area under the curve

y = sin x    ........(1)

and

y = sin 2x     ............(2)

Between x = 0 and x = \frac{\pi}{3}

x y = sin x	0\ \ \ \ \ \ \frac{\pi}{6}\ \ \ \ \ \ \frac{\pi}{4}\ \ \ \ \ \ \ \frac{\pi}{3}\\ 0\ \ \ \ \  0.5\ \ \ \  0.7\ \ \ \ 0.8	\frac{\pi}{2}\\ 1
y = sin 2x	0      0.8       1       0.8	0

Here is the rough sketch 

Area under curve y = sin 2x

Shaded region represents the required area.

We slice it into approximation rectangle of 

Width = △x

Length = y1

Area of rectangle = y1△x

The approx rectangles slide from x = 0 to x = \frac{\pi}{3}     ,

Thus,

Required area = Region OPACO

\displaystyle A_1=\int_0^{\frac{\pi}{3}}y_1\ dx\\ =\int_0^{\frac{\pi}{3}}sin\ 2x\ dx\\ =\left[\frac{-cos\ 2x}{2}\right]_0^{\frac{\pi}{3}}\\ =-\left[-\frac{1}{4}-\frac{1}{2}\right]\\ A_1=\frac{3}{4}\ sq.\ units

We slice it into approximation rectangle of 

Width = △x

Length = y2

Area of rectangle = y2△x

The approx rectangles slide from x = 0 to x = \frac{\pi}{3},

Thus,

Required area = Region OQACO

\displaystyle =\int_0^{\frac{\pi}{3}}y_2\ dx\\ =\int_0^{\frac{\pi}{3}}sin\ x\ dx\\ =\left[{-cos\ x}\right]_0^{\frac{\pi}{3}}\\ =-\left[\frac{1}{2}-1\right]\\ A_2=\frac{1}{2}\ sq.\ units

Thus,

A_2:A_1=\frac{1}{2}:\frac{3}{4}\\ A_2:A_1=2:3

Question 25. Compare the area under the curves y = cos²x and y = sin²x between x = 0 and x = π

Solution:

Here to compare area under curves

y = cos²x

and

y = sin²x

Between x = 0 and x = π

This is the table for y = cos²x and y = sin²x

x y = cos2x	0 1	\frac{\pi}{6}\ \ \ \ \ \ \ \ \ \frac{\pi}{4}\\ 0.75\ \ \ \ 0.5	\frac{\pi}{3}\ \ \ \ \ \ \ \ \ \frac{\pi}{2}\\ 0.25\ \ \ \ \ 0	\frac{2\pi}{3}\ \ \ \ \ \ \ \ \ \frac{3\pi}{4}\\ 0.25\ \ \ \ \ \ 0.5	\frac{5\pi}{6}\ \ \ \ \ \ \ \ \ \pi\\ 0.75\ \ \ \ \ 1
y = sin2x	0	0.25          0.5	0.75      1	0.75     0.5	0.25       0

Area of region enclosed by

y = cos²x and axis

A₁ = Region OABO + Region BCDB

= 2(Region BCDB)

\displaystyle =2\int_{\frac{\pi}{2}}^\pi cos^2x\ dx\\ =2\int_{\frac{\pi}{2}}^\pi\left(\frac{1-cos\ 2x}{2}\right)\ dx\\ =\left[x-\frac{sin\ 2x}{2}\right]^\pi_{\frac{\pi}{2}}\\ =\left[(x-0)-\left(\frac{\pi}{2}-0\right)\right]\\ =\pi-\frac{\pi}{2}\\ A_1=\frac{\pi}{2}\ sq.\ units\ \ \ \ \ \ .....(1)    

Area of region enclosed by y = sin²x and axis

A₂ = Region OEDO

\displaystyle =\int_{0}^\pi sin^2x\ dx\\ =\int_{0}^\pi\left(\frac{1-cos\ 2x}{2}\right)\ dx\\ =\frac{1}{2}\left[x-\frac{sin\ 2x}{2}\right]^\pi_{0}\\ =\frac{1}{2}[(x-0)-(0)]\\ A_2=\frac{\pi}{2}\ sq.\ units\ \ \ \ \ \ .....(2)

From equation (1) and (2),

A₁ = A₂

Thus,

Area enclosed by y = cos²x = Area enclosed by y = sin²x.

Question 26. Find the area bounded by the ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=1  and the ordinates x = 0 and x = ae, where, b² = a²(1 - e ²) and e < 1.

Solution:

Thus, the required area in the figure below of the region BOB'RFSB is enclosed by the ellipse and the lines x = 0 and x = ae

Here is the area of the region BOB'RFSB

\displaystyle =2\int_0^{ae}y\ dx\\ =2\frac{b}{a}\int_0^{ae}\sqrt{a^2-x^2}\ dx\\ =\frac{2b}{a}\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^{ae}\\ =\frac{2b}{2a}\left[ae\sqrt{a^2-a^2e^2}+a^2sin^{-1}e\right]\\ =ab\left[e\sqrt{1-e^2}+sin^{-1}e\right]

Question 27. Find the area of the minor segment of the circle x² + y² = a² cut-off by the line x = \frac{a}{2}  .

Solution:

Area of the mirror segment of the circle

\displaystyle =2\int_{\frac{a}{2}}^a\sqrt{a^2-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{2}\right]_{\frac{a}{2}^a}\\ =2\left[\frac{a}{2}(0)+\frac{a^2}{2}sin^{-1}\left(\frac{a}{2}\right)-\frac{a}{4}\sqrt{a^2-\frac{a^2}{4}}-\frac{a^2}{2}sin^{-1}\frac{a}{4}\right]\\ =2\left[\frac{a^2}{2}sin^{-1}\left(\frac{a}{2}\right)-\frac{a}{4}\sqrt{a^2-\frac{a^2}{4}}-\frac{a^2}{2}sin^{-1}\frac{a}{4}\right]\\ =\frac{a^2}{12}[4\pi-3\sqrt3]\ sq.\ units

Question 28. Find the area of the region bounded by the curve x = at, y = 2at between the ordinates corresponding t = 1 and t = 2.

Solution:

Area of the bounded region

\displaystyle =2\int_1^2y\ \frac{dx}{dt}\ dt\\ =2\int_1^2(2at)(2at)\ dt\\ =8a^2\int_1^2t^2\ dt\\ =8a^2\left[\frac{t^3}{3}\right]_1^2\\ =8a^2\left[\frac{8}{3}-\frac{1}{3}\right]\\ =\frac{56a^2}{3}\ sq.\ units

Question 29. Find the area enclosed by the curve x = 3 cos t, y = 2 sin t.

Solution:

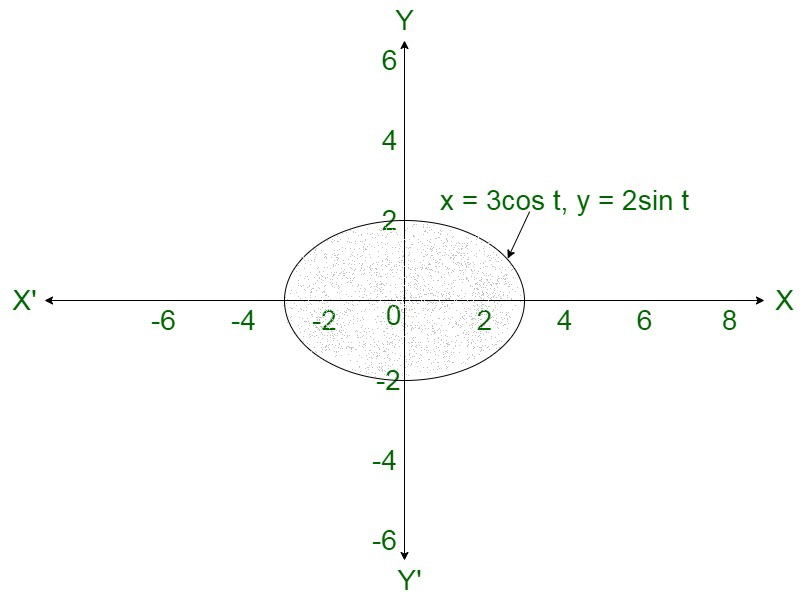
Area of the bounded region

\displaystyle =4\int_0^{\frac{\pi}{2}}2sin\ t\ dt\\ =-8[cos\ t]_0^{\frac{\pi}{2}}

= -8 [0 - 1]

= 8 square units 

Read More:

• Area Between Two Curves: Formula, Definition and Examples
• Area Under Curve

Practice Questions

1. Find the area of the region bounded by the curve y = x^2 and the lines y = 1, x = 0, and x = 2.

2. Calculate the area enclosed by the parabola y^2 = 4x and the line x = 3.

3. Determine the area of the region bounded by the curve y = sin x, the x-axis, and the lines x = 0 and x = π.

4. Find the area of the region lying above the x-axis and bounded by the curve y = cos x from x = 0 to x = π.

5. Calculate the area enclosed by the ellipse (x^2/16) + (y^2/9) = 1.

6. Determine the area of the region bounded by the curve y = √x, the y-axis, and the line y = 2.

7. Find the area of the region enclosed by the parabola x = y^2 and the line y = x - 2.

8. Calculate the area of the region bounded by the curve y = e^x, the x-axis, and the lines x = 0 and x = 1.

9. Determine the area of the region bounded by the curve y = x^3 - 3x + 2 and the x-axis between its points of intersection with the x-axis.

10. Find the area of the region bounded by the curves y = x^2 and y = x^3 in the first quadrant.

Summary

Chapter 21 of RD Sharma's Class 12 mathematics textbook focuses on Areas of Bounded Regions. Exercise 21.1 specifically deals with finding areas bounded by curves and lines. Key points covered in this exercise include:

1. Using definite integrals to calculate areas under curves

2. Finding areas bounded by a curve and coordinate axes

3. Calculating areas between a curve and a line

4. Determining areas enclosed by two curves

5. Applying the concept of symmetry to simplify calculations

6. Handling different types of functions (polynomial, trigonometric, exponential)

7. Identifying and using appropriate limits of integration

8. Interpreting the geometric meaning of integrals in area problems

This exercise builds on fundamental integration techniques and applies them to practical area calculation problems, which is crucial for understanding many applications in physics, engineering, and advanced mathematics.