Class 12 RD Sharma Solutions - Chapter 21 Areas of Bounded Regions - Exercise 21.2

Areas of Bounded Regions" typically refers to the mathematical calculation of the area enclosed by curves or lines on a coordinate plane. This concept is fundamental in calculus, particularly in the context of definite integrals.

Question 1. Find the area in the first quadrant bounded by the parabola y = 4x² and the lines x = 0, y = 1, and y = 4.

Solution:

From the question it is given that,

Lines, x = 0, y = 1, y = 4

Parabola y = 4x² … [equation (i)]

So, equation (i) represents a parabola with vertex (0, 0) and axis as y – axis. x = 0 is y – axis and y = 1, y = 4 are line parallel to x – axis passing through (0, 1) and (0, 4) respectively, as shown in the rough sketch below,

Now, we have to find the area of ABCDA,

Then, the area can be found by taking a small slice in each region of width Δy,

And length = x

The area of sliced part will be as it is a rectangle = x Δy

So, this rectangle can move horizontal from y = 1 to x = 4

The required area of the region bounded between the lines = Region ABCDA

\displaystyle=\int_1^4xdy

Given, y = 4x²

x = \displaystyle\sqrt{\frac{y}{4}}\\ \int_1^4\sqrt{\frac{y}{4}}\ dy\\ \frac{1}{2}\int_1^4\sqrt y\ dy

On integration, we get,

\displaystyle=\frac{1}{2}\left[\frac{2}{3}y\sqrt y\right]_1^4

Now, applying limits we get,

= \frac{1}{2} \left[\left(\frac{2}{3} × 4 × \sqrt4\right) – \left(\frac{2}{3} × 1 × \sqrt1\right)\right]\\ = \frac{1}{2} \left[\frac{16}{3} – \frac{2}{3}\right]\\ = \frac{1}{2} \left[\frac{(16 – 2)}{3}\right]\\ = \frac{1}{2} \left[\frac{14}{3}\right]\\ = \frac{7}{3}

Therefore, the required area is \frac{7}{3}  square units.

Question 2. Find the area of the region bounded by x² = 16y, y = 1, y = 4, and the y-axis in the quadrant.

Solution:

From the question it is given that,

Region in first quadrant bounded by y = 1, y = 4

Parabola x² = 16y … [equation (i)]

So, equation (i) represents a parabola with vertex (0, 0) and axis as y-axis, as shown in the rough sketch below,

Now, we have to find the area of ABCDA,

Then, the area can be found by taking a small slice in each region of width Δy,

And length = x

The area of sliced part will be as it is a rectangle = x Δy

So, this rectangle can move horizontal from y = 1 to x = 4

The required area of the region bounded between the lines = Region ABCDA

\displaystyle\int_1^4x\ dy

Given, x² = 16y

x=\sqrt{16y}\\ x=4\sqrt{y}\\ =\int_1^44\sqrt4\ dy  

On integrating we get,

=4\left[\frac{2}{3}y\sqrt y\right]^4_1\\ =\int_1^4x\ dy

Given, x² = 16y

x=\sqrt{16y}\\ x=4\sqrt{y}\\ =\int_1^44\sqrt4\ dy

On integrating we get,

=4\left[\frac{2}{3}y\sqrt y\right]^4_1\\ =\int_1^4x\ dy

Now, applying limits we get,

= 4 \left[\left(\frac{2}{3} × 4 × \sqrt4\right) – \left(\frac{2}{3}× 1 × \sqrt1\right)\right]\\ = 4 \left[\frac{16}{3} – \frac{2}{3}\right]\\ = 4 \left[\frac{(16 – 2)}{3}\right]\\ = 4 \left[\frac{14}{3}\right]\\ = \frac{56}{3}

Therefore, the required area is \frac{56}{3}  square units.

Question 3. Find the area of the region bounded by x² = 4ay and its latus rectum. 

Solution:

We have to find the area of the region bounded by x² = 4ay

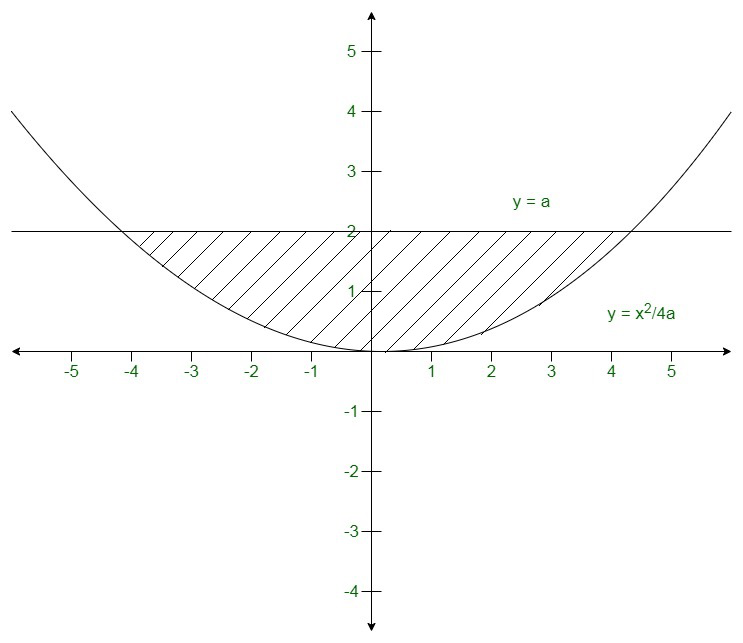
Then,

Area of the region = \displaystyle2\times\int_0^{2a}\left(a-\frac{x^2}{4a}\right)dx

On integrating we get,

= 2\times\left[ax-\frac{x^3}{12a}\right]_0^{2a}

Now applying limits,

= 2 × \left[(a (2a – 0)) – \frac{((2a)^3 – 0^3)}{12a}\right]\\ = 2 × \left[(2a^2) – \frac{8a^3}{12a}\right]\\ = 2 × \left[\frac{(24a^3 – 8a^3)}{12a}\right]\\ = 2 × \left[\frac{16a^3}{12a}\right]\\ = 2 × \left[\frac{4a^2}{3}\right]\\ = \frac{8a^2}{3}\\

Therefore, the area of the region is \frac{8a^2}{3}  square units.

Question 4. Find the area of the region bounded by x² + 16y = 0 and its latus rectum. 

Solution:

We have to find the area of the region bounded by x² + 16y = 0

Then, 

Area of the region = \displaystyle2\times\int_0^{8}\left[-\frac{x^2}{16}-(-4)\right]dx

On integrating we get,

= 2\times\left[4x-\frac{x^3}{48}\right]_0^{8}

Now applying limits,

= 2 × \left[(4 (8 – 0)) – \frac{((8)^3 – 0^3)}{48}\right]\\ = 2 × \left[(32) – \frac{512}{48}\right]\\ = 2 × \left[(32)-\frac{32}{3}\right]\\ = 2 × \left[\frac{96-32}{3}\right]\\ = 2 × \left[\frac{64}{3}\right]\\ = \frac{128}{3}\\

Therefore, the area of the region is  \frac{128}{3}  square units.

Question 5. Find the area of the region bounded by the curve ay² = x³, the y-axis, and the lines y = a and y = 2a.

Solution:

We have to find the area of the region bounded by curve ay² = x³, and lines y = a and y = 2a.

Then,

Area of the region = \displaystyle\int_a^{2a}(ay^2)^{\frac{1}{3}}\ dy\\ =a^{\frac{1}{3}}\int_a^{2a}y^{\frac{2}{3}}dy

On integrating we get, = a^{\frac{1}{3}}\left[\frac{3}{5}y^{\frac{5}{3}}\right]_0^{2a}

Now applying limits we get, = \frac{3}{5}\left(2^{\frac{5}{3}}-1\right)a^2\ sq\ units

Practice Questions

1. Find the area of the region bounded by the parabola y = x^2 - 4x + 3 and the x-axis.

2. Calculate the area enclosed by the curve y = sin x and the x-axis from x = 0 to x = π.

3. Determine the area of the region bounded by the curve y = |x - 1| and the x-axis from x = -1 to x = 3.

4. Find the area of the region bounded by the curve y = x^3 - 3x + 2 and the x-axis.

5. Calculate the area enclosed by the curve y = e^x and the x-axis from x = 0 to x = ln 2.

6. Determine the area of the region bounded by the curve y = √(4 - x^2) and the x-axis.

7. Find the area of the region bounded by the curve y = cos x and the x-axis from x = -π/2 to x = π/2.

8. Calculate the area enclosed by the curve y = x^2 - 5x + 6 and the x-axis.

9. Determine the area of the region bounded by the curve y = ln x and the x-axis from x = 1 to x = e.

10. Find the area of the region bounded by the curve y = x^3 - x and the x-axis.

Summary

Chapter 21 of RD Sharma's Class 12 mathematics textbook, specifically Exercise 21.2, focuses on calculating the areas of regions bounded by curves and the x-axis.

Key points covered in this exercise include:

1. Using definite integrals to calculate areas

2. Identifying the points where a curve intersects the x-axis

3. Handling curves that cross the x-axis multiple times

4. Dealing with absolute value functions in area calculations

5. Applying the concept of even and odd functions to simplify calculations

6. Understanding the significance of positive and negative areas

7. Utilizing symmetry to reduce computational complexity

8. Interpreting the geometrical meaning of the calculated areas

This exercise builds on the fundamental concepts of integration and applies them to practical problems involving area calculations. It's crucial for understanding many applications in physics, engineering, and advanced mathematics.