Class 12 RD Sharma Solutions- Chapter 21 Areas of Bounded Regions - Exercise 21.4

Chapter 21 of RD Sharma’s Class 12 Mathematics textbook delves into the concept of the Areas of Bounded Regions. This chapter explores the various techniques to calculate the areas of the regions enclosed by the curves and lines. Exercise 21.4 focuses on applying these concepts to solve practical problems involving bounded regions.

Areas of Bounded Regions

The study of areas of the bounded regions involves calculating the area of a region enclosed by curves or lines. These areas are often bounded by the intersections of different functions such as the lines and parabolas or circles. The process typically involves finding points of the intersection and integrating the functions over the bounded region. Understanding this concept is crucial for solving real-world problems where accurate area calculations are required.

Question 1. Find the area of the region between the parabola x = 4y − y² and the line x = 2y − 3.

Solution: 

Area of the bounded region

=\int_{-1}^{3}(4y-y^2-2y+3)dy\\ =[2\frac{y^2}{2}-\frac{y^3}{3}+3y]_{-1}^{3}\\ =9-9+9-1-\frac{1}{3}+3-\frac{(16a)^3}{48a}\\ =\frac{32}{3}sq.\ units

Question 2. Find the area bounded by the parabola x = 8 + 2y − y²; the y-axis and the lines y = −1 and y = 3.

Solution: 

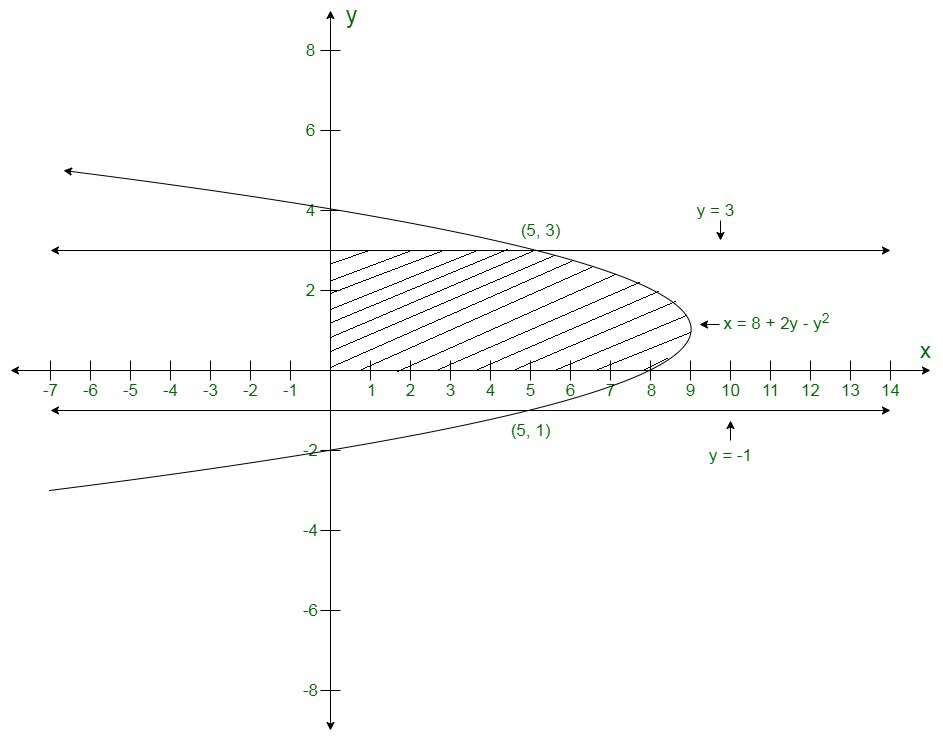
Area of the bounded region

=\int_{-1}^{3}(5-0)dy+\int_{-1}^{3}8+2y-y^2-5\ dy\\ =[5y]_{-1}^{3}+[3y+y^2-\frac{y^3}{3}]_{-1}^{3}\\ =15+5+9+9-\frac{27}{3}+3-1-\frac{1}{3}\\ =\frac{92}{3}sq.\ units

Question 3. Find the area bounded by the parabola y² = 4x and the line y = 2x − 4.

(i) By using horizontal strips

(ii) By using vertical strips

Solution:

Area of the bounded region

=\int_{-2}^{4}(\frac{y+4}{2}-\frac{y^2}{4})\ dy\\ =[\frac{y^2}{4}+2y-\frac{y^3}{12}]_{-2}^{4}\\ =4+8-\frac{16}{3}-1+4-\frac{2}{3}\\ =9\ sq.\ units

Question 4. Find the area of the region bounded the parabola y² = 2x and straight line x − y = 4.

Solution: 

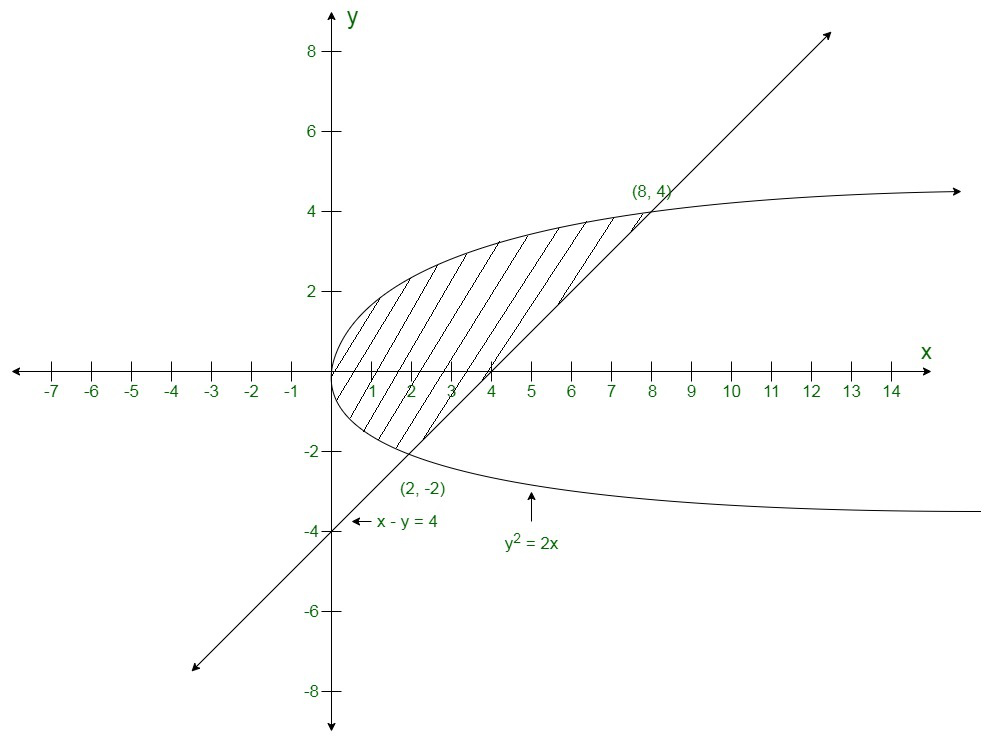
Area of the bounded region

=\int_{-2}^{4}(y+4-\frac{y^2}{2})\ dy\\ =[\frac{y^2}{2}+4y-\frac{y^3}{6}]_{-2}^{4}\\ =8+16-\frac{32}{3}-2+8-\frac{4}{3}\\ =18\ sq.\ units

Read more:

• Area Between Two Curves: Formula, Definition and Examples
• Area Under Curve

Summary

Chapter 21 of RD Sharma's Class 12 mathematics textbook focuses on Areas of Bounded Regions. Key points covered in this chapter include:

• Concept of area under a curve
• Area bounded by a curve and the x-axis
• Area between two curves
• Use of definite integrals to calculate areas
• Techniques for finding points of intersection of curves
• Application of symmetry to simplify area calculations
• Areas of common shapes (circles, ellipses) using integration
• Solving word problems involving areas of bounded regions

This chapter builds on the concepts of integration and applies them to practical problems involving area calculations. It's crucial for understanding many applications in physics, engineering, and advanced mathematics.