Class 8 RD Sharma Solutions- Chapter 20 Area Of Trapezium And Polygon- Exercise 20.1 | Set 1

RD Sharma Solutions for Class 8, Chapter 20 covers the Area of Trapezium and Polygon. This chapter focuses on calculating the areas of trapeziums and various polygons, building upon students' existing knowledge of basic geometric shapes. The solutions provide step-by-step explanations to help students understand the concepts and solve problems effectively.

What is the Area of the Trapezium and Polygon

A trapezium is a quadrilateral with at least one pair of parallel sides. Its area can be calculated using the formula: Area = 1/2(a+b)h, where 'a' and 'b' are the lengths of the parallel sides and 'h' is the height. A polygon is a closed figure with three or more straight sides. The area of a polygon can be found by dividing it into triangles or using specific formulas depending on the type of polygon.

Question 1. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m²?

Solution: 

Given that,

Base of parallelogram = 24cm,

Height of parallelogram = 10cm,

Area of floor = 1080m²

As we know that,

Area of parallelogram = Base × Height

Area of 1 tiles = 24 × 10 = 240 cm²

As we know that 1m = 100cm,

So area will be 1080 m2 = 1080 × 100 × 100 cm²

Number of tiles required = Area of floor / Area of 1 tile

Number of tiles required = (1080 × 100 × 100) / (24 × 10) = 45000

Hence, Number of tiles required is 45000.

Question 2. A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Figure. If AB = 60 m and BC = 28 m, Find the area of the plot.

Solution: 

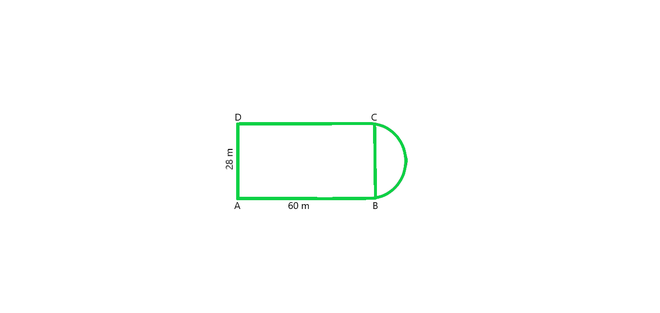
From figure, we conclude that, Area of the plot = Area of the rectangle + Area of semi-circle

Radius of semi-circle = BC/2 = 28/2 = 14m

As we know that Area of the Rectangular plot = Length × Breadth = 60 × 28 = 1680 m²

Area of the Semi-circular portion = πr²/2

= 1/2 × 22/7 × 14 × 14 = 308 m²

Hence, the total area of the plot = 1680 + 308 = 1988 m²

Question 3. A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π= 22/7.)

Solution: 

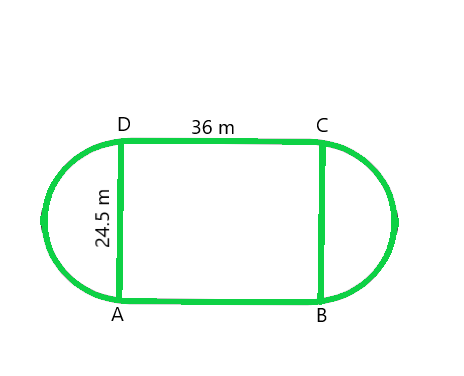
From figure, we conclude that, Area of the plot = Area of the Rectangle + 2 × area of one semi-circle

Radius of semi-circle = BC/2 = 24.5/2 = 12.25m                                (Given)

As we know that Area of the Rectangular plot = Length × Breadth = 36 × 24.5 = 882 m²

and Area of the Semi-circular portions = 2 × πr²/2

= 2 × 1/2 × 22/7 × 12.25 × 12.25 = 471.625 m²

Hence, the total Area of the plot = 882 + 471.625 = 1353.625 m²

Question 4. A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.

Solution: 

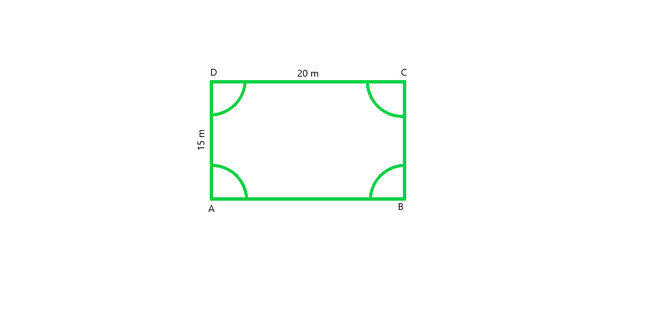
From figure, we conclude that, Area of the plot = Area of the rectangle – 4 × area of one quadrant

Radius of semi-circle = 3.5 m                                        (Given)

Area of four quadrants = area of one circle                        (from figure)

Area of the plot = Length × Breadth – πr²

Hence, Area of the plot = 20 × 15 – (22/7 × 3.5 × 3.5) = 261.5 m²

Question 5. The inside perimeter of a running track (shown in Fig. 20.24) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

Solution: 

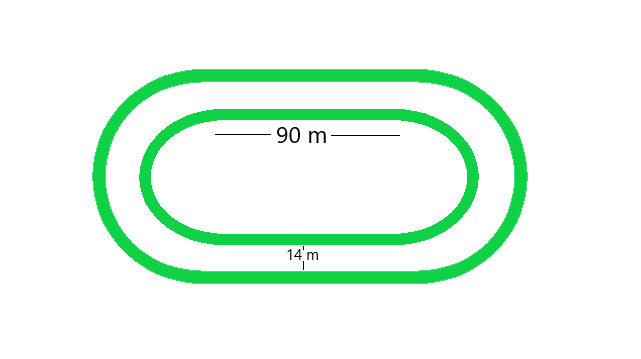
From figure, we conclude that, Perimeter of the inner track = 2 × Length of rectangle + perimeter of two semi-circular ends

Perimeter of the inner track = Length + Length + 2πr

400 = 90 + 90 + (2 × 22/7 × r)

(2 × 22/7 × r) = 400 – 180

(2 × 22/7 × r) = 220

44r = 220 × 7

44r = 1540

r = 1540/44 = 35

r = 35m

Hence, the radius of inner circle = 35 m

Now we have to calculate the radius of outer track

Radius of outer track = Radius of inner track + width of the track                                     (from figure)

Radius of outer track = 35 + 14 = 49m                                   (given)

Length of outer track = 2× Length of rectangle + perimeter of two outer semi-circular ends

Length of outer track = 2× 90 + 2πr

Length of outer track = 2× 90 + (2 × 22/7 × 49)

Length of outer track = 180 + 308 = 488

Hence, the Length of outer track = 488m

Area of inner track = Area of inner rectangle + Area of two inner semi-circles

Area of inner track = Length × Breadth + πr²

Area of inner track = 90 × 70 + (22/7 × 35 × 35)

Area of inner track = 6300 + 3850

Hence, the Area of inner track = 10150 m²

Area of outer track = Area of outer rectangle + Area of two outer semi-circles

Breadth of outer track = 35 + 35 +14 + 14 = 98 m

Area of outer track = length× breadth + πr²

Area of outer track = 90 × 98 + (22/7 × 49 × 49)

Area of outer track = 8820 + 7546

Hence, Area of outer track = 16366 m²

Now, we have to calculate the Area of path

Area of path = Area of outer track – Area of inner track

Area of path = 16366 – 10150 = 6216

Hence, Area of path is 6216 m²

Question 6. Find the area of Fig., in square cm, correct to one place of decimal. (Take π =22/7)

Solution:

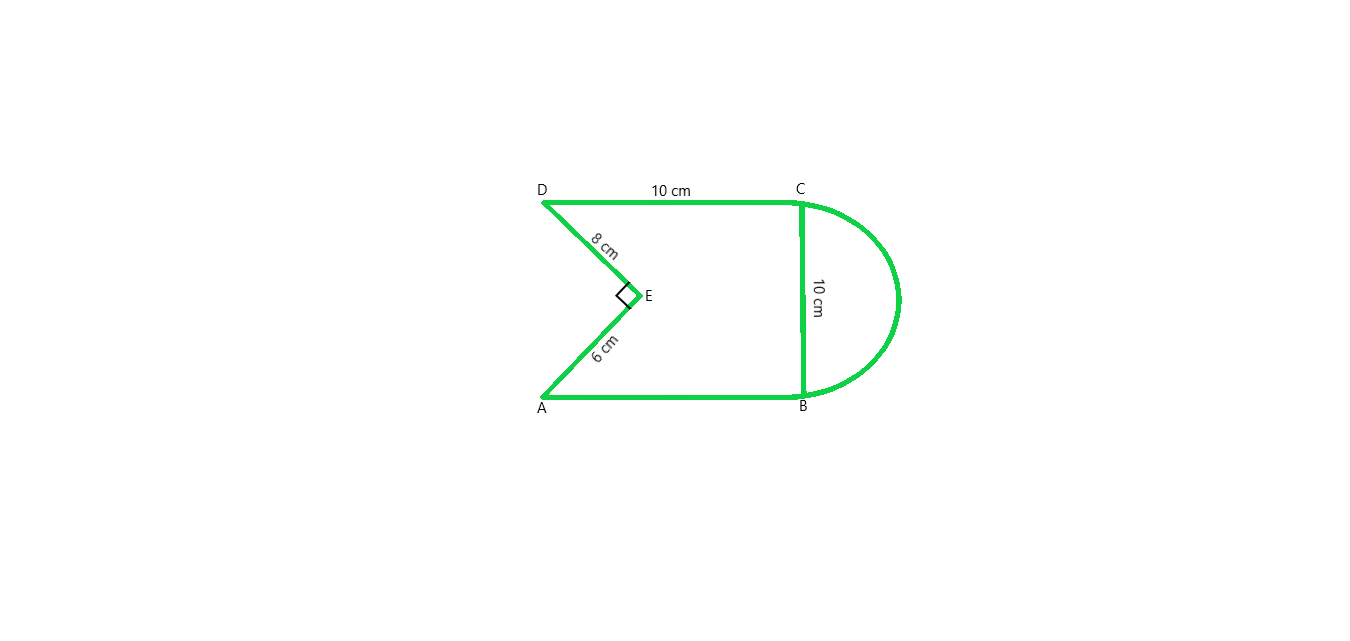
From figure we conclude that, Area of the Figure = Area of square + Area of semi-circle – Area of right angled triangle

Area of the Figure = side × side + πr²/2 – (1/2 × base × height)

put the values in formula and we get,

Area of the Figure = 10 × 10 + (1/2 × 22/7 × 5 × 5) – (1/2 × 8 × 6)

Area of the Figure = 100 + 39.28 – 24

Area of the Figure = 115.3

Hence, Area of the Figure = 115.3 cm²

Question 7. The diameter of a wheel of a bus is 90 cm which makes 315 revolutions per minute. Determine its speed in kilometres per hour. (Take π=22/7)

Solution: 

Given that,

Diameter of a wheel = 90 cm,

As we know that, Perimeter of wheel = πd

Perimeter of wheel = 22/7 × 90 = 282.857

Hence, the Perimeter of a wheel = 282.857 cm

Distance covered in 315 revolutions = 282.857× 315 = 89099.955 cm

As we know that 1 km = 100000 cm

So, The Distance covered = 89099.955/100000 = 0.89 km

Speed in km per hour = 0.89 × 60 = 53.4 km per hour.

Question 8. The area of a rhombus is 240 cm^2 and one of the diagonal is 16 cm. Find another diagonal.

Solution: 

Given that,

Area of rhombus = 240 cm^2,

Diagonal = 16 cm. 

As we know that,

Area of rhombus = 1/2 × d1 × d2

240 = 1/2 × 16 × d2

240 = 8 × d2

d2 = 240/8 = 30

Hence the other diagonal is 30 cm.

Question 9. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.

Solution: 

Given that,

Diagonal(d1) = 7.5 cm,

Diagonal(d2) = 12 cm.

As we know that,

Area of rhombus = 1/2 × d1 × d2

Area of rhombus = 1/2 × 7.5 × 12

Area of rhombus = 6 × 7.5 = 45

Hence, Area of rhombus = 45 cm²

Question 10. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

Solution: 

As we know that,

Area of quadrilateral = 1/2 × d1 × (p1 + p2)

Area of quadrilateral = 1/2 × 24 × (8 + 13)

Area of quadrilateral = 12 × 21 = 252

Hence, Area of quadrilateral is 252 cm²

Question 11. Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.

Solution: 

Given that,

Side of rhombus = 6 cm,

Altitude of rhombus = 4 cm.

As we know that rhombus is a parallelogram, therefore area of parallelogram = base × altitude

Therefore, Area of parallelogram = 6 × 4 = 24 cm²

Area of parallelogram = Area of rhombus

Area of rhombus = 1/2 × d1 × d2

24 = 1/2 × 8 × d2

24 = 4 × d2

d2 = 24/4 = 6

Hence, the length of other diagonal of rhombus is 6 cm.

Summary

Chapter 20 of RD Sharma Solutions for Class 8 focuses on calculating areas of trapeziums and polygons. It provides formulas and techniques to solve various problems involving these shapes, enhancing students' understanding of geometry and spatial reasoning. The chapter covers different types of polygons, including regular and irregular shapes, and offers practical applications of area calculations in real-world scenarios.