The complement of a set is the set that consists of all the elements from the universal set that are not already included in the given set. In other words, the difference between the universal set and the given set represents the complement of that set.
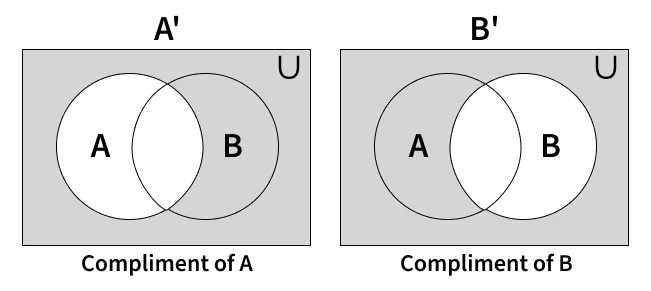 Compliment of Set A and B
Compliment of Set A and BThe complement of a set A is mathematically expressed as:
A' = {x ∈ U and x ∉ A}
Where x denotes the elements in Universal Set, U but not in A.
How to Find the Complement of a Set?
The complement of a set is simply found by excluding the elements of the given set from the universal set.
Example: Find the complement of set S = {4, 8, 12, 16}, where the universal set is all multiples of 4 that are smaller than 50.
Solution:
Step 1: Identify the universal set (U) and the set (S) for which you want to find the complement.
Universal Set(U) = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48}
Also, given: S = {4, 8, 12, 16}
Step 2: Calculate the complement of set S by excluding the elements of S from the universal set U i.e., S' = U - S.
S' = U - S = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48} - {4, 8, 12, 16}
Step 3: Simplify the resulting set to obtain the complement.
Thus, S' = {20, 24, 28, 32, 36, 40, 44, 48}
Properties of Complement of a Set
There are various properties of the Complement of a Set; some of these properties are discussed as follows:
Complement Laws
- The union of set S and its complement set S' is the universal set, i.e., S ∪ S’ = U.
Example: If U = {10, 11, 12, 13, 14} and S = {10, 11, 12}; then S' = {13, 14}.
- The intersection of set S and its complement set S' is the null or empty set, i.e., S ∩ S’ = ∅.
Example: If U = {10, 11, 12, 13, 14} and S = {10, 11, 12}; then S' = {13, 14}.
Now, S ∩ S’ = {10, 11, 12} ∩ {13, 14} = ∅.
Law of Double Complementation
- The complement of the complement of a given set is the set itself, i.e., (S')' = S.
Example: If U = {10, 11, 12, 13, 14} and S = {10, 11, 12}; then S' = {13, 14}.
The complement of S' = U - S' = {10, 11, 12} = set S.
Law of Null and Universal Sets
Example: If U = {10, 11, 12, 13, 14}; then U' = ∅ and ∅' = U.
De Morgan’s laws
- The complement of the union of two sets is equal to the intersection of the complements of the two sets, i.e., (S U T)’ = S’ ∩ T’.
Example: If U = {10, 11, 12, 13, 14} and S = {13, 14} and T = {10, 11}.
Now, S ∪ T = {10, 11, 13, 14} and (S ∪ T)' = {12}.
Thus, S’ ∩ T’ = {10, 11, 12} ∩ {12, 13, 14} = {12} = (S ∪ T)'.
- The complement of the intersection of two sets is equal to the union of the complements of the two sets, i.e., (S ∩ T)’ = S’ U T’.
Example: If U = {10, 11, 12, 13, 14} and S = {13, 14} and T = {10, 11}.
Now, S ∩ T = ∅ and (S ∩ T)’ = {10, 11, 12, 13, 14}.
Thus, S’ ∪ T’ = {10, 11, 12} ∪ {12, 13, 14} = {10, 11, 12, 13, 14} = S’ ∪ T’.
Solved Examples on Complement of a Set
Learn various Practice Questions on Complement of a Set.
Question 1. If D = { x | x is a multiple of 10, x ∈ N }, find D'.
Solution:
Given: the universal set U = set of all natural numbers = N = {1, 2, 3, 4, 5, 6,....}
Also it is given that: D = { x | x is a multiple of 10, x ∈ N }
⇒ D = {10, 20, 30, 40, 50, 60,....}
⇒ D' = U - D
D' = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12,...19, 21, 22,..., 29, 31,.....}.
Question 2. If S and T are any two sets, prove that S' – T' = T – S.
Solution:
S' – T' = T – S is only possible when S' – T' ⊆ S – T.
Let x ∈ S' – T'
⇒ x ∈ S' and x ∉ T'
⇒ x ∉ S and x ∈ T (since, S ∩ S' = ϕ )
⇒ x ∈ S – T
The above result would be true for all x ∈ S' – T'
∴ S' – T' = T – S
Question 3. How many elements are there in the complement of the set of all vowels in the English alphabet?
Solution:
The English alphabet consists of 26 alphabets of which 5 are vowels and 21 are consonants. The difference between the universal set(U) and the set of vowels(say, V) is the complement of the set of all vowels.
Now, n(U) = 26 and n(V) = 5.
Thus, n(V') = n(U) - n(V)
⇒ n(V') = 26 - 5
⇒ n(V') = 21
Question 4. If P and Q are two sets, then prove P ∩ (P' ∪ Q') = P ∩ Q.
Solution:
LHS = P ∩ (P' ∪ Q')
Let us expand the LHS to get: (P ∩ P’) ∪ (P ∩ Q)
Since, P ∩ P’ = ϕ; our LHS becomes:
LHS = ϕ ∪ (P ∩ Q)
⇒ LHS = P ∩ Q
Thus, LHS = RHS
Hence Proved.
Question 5. If U = {12, 13, 15, 17, 19} and S = {13, 17}, T = {12, 15, 17, 19}, then prove that (S ∪ T)' = S' ∩ T'.
Solution:
LHS = (S ∪ T)'. Let us first find S ∪ T.
S ∪ T = {12, 13, 15, 17, 19} = U
⇒ (S ∪ T)' = U – (S ∪ T) = U – U = ϕ.
So, LHS = ϕ.
RHS = S' ∩ T'
S' = U – S = {12, 15, 19}
and T' = U – T = {13}
⇒ S' ∩ T' = {12, 15, 19} ∩ {13} = ϕ
So, RHS = ϕ
Thus, LHS = RHS
Hence Proved.
Question 6. If X and Y are two sets, prove that: X – (X – Y) = X ∩ Y.
Solution:
According to the De Morgan's Laws, (A ∪ B)’ = A’ ∩ B’ and (A ∩ B) ‘ = A’ ∪ B’.
LHS = X – (X – Y)
⇒ LHS = X ∩ (X – Y)'
⇒ LHS = X ∩ (X ∩ Y')'
⇒ LHS = X ∩ (X' ∪ Y')') ((Y')' = Y)
⇒ LHS = X ∩ (X' ∪ Y)
⇒ LHS = (X ∩ X') ∪ (X ∩ Y)
⇒ LHS = ϕ ∪ (X ∩ Y)
⇒ LHS = (X ∩ Y) [As ϕ ∪ A = A]
But, RHS = (X ∩ Y)
∴ LHS = RHS
Hence Proved.
Practice Questions on Complement of a Set
Question 1: Let A = {1, 2, 3, 4, 5} and the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Find the complement of A, i.e., A'.
Question 2: If M = {a, b, c, d} and N = {c, d, e, f}, prove that: (M ∪ N)' = M' ∩ N'.
Question 3: The universal set U consists of all positive integers less than or equal to 20. If A = {2, 4, 6, 8, 10} and B = {1, 2, 3, 4, 5, 6}, find the complement of A ∩ B.
Question 4: If X = {3, 5, 7, 9}, Y = {1, 3, 5, 7}, and the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, find X' – Y.
Question 5: Let U = {10, 20, 30, 40, 50}, P = {20, 40}, and Q = {30, 50}. Find (P ∪ Q)'.
Question 6: If A = {2, 4, 6, 8, 10} and B = {1, 2, 3, 4, 5, 6}, find the number of elements in the complement of the union of A and B, i.e., (A ∪ B)'.
Question 7: If X = {a, b, c} and Y = {b, c, d}, and the universal set U = {a, b, c, d, e}, find the complement of (X ∩ Y).
Question 8: Prove that: (X ∩ Y)' = X' ∪ Y'
Question 9: If A = {1, 3, 5, 7, 9}, B = {2, 4, 6, 8, 10}, and the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, find A' ∩ B'.
Question 10: If the universal set U = {1, 2, 3, 4, 5, 6}, and A = {2, 3, 4}, find the number of elements in A' and B = {1, 5, 6}.
Explore
Maths
4 min read
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice