The equation of a line describes the relationship between the x-coordinates and y-coordinates of all points that lie on the line. It provides a way to mathematically represent that straight path.
In general, the equation of a straight line can be written in several forms, depending on the information you have about the line.
The most common form is the slope-intercept form:
y = mx + b
where:
- m → slope of the line (the measure of its steepness)
- b → y-intercept (the point where the line crosses the y-axis)
Suppose we have a straight line containing the following points:
x-axis values | 0 | 1 | 2 | 3 | 4 | 5 |
|---|
y-axis values | 1 | 3 | 5 | 7 | 9 | 11 |
|---|
The graph of the equation will be :
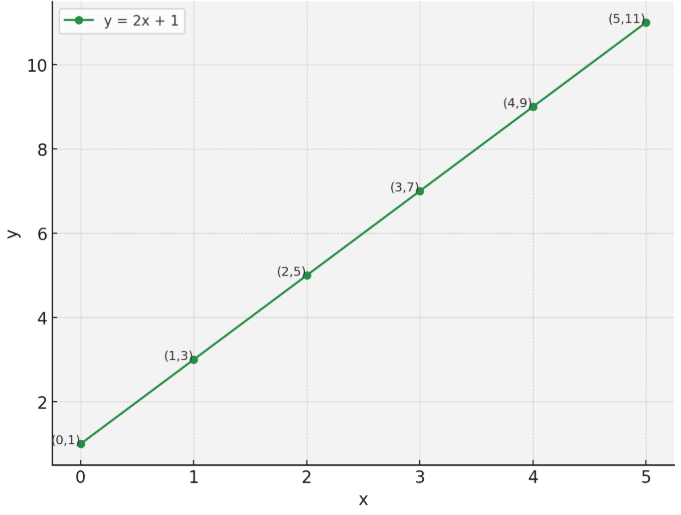
At first glance, we can see there is a pattern: for every increase of 1 in the x-value, the y-value increases by 2. Specifically, if you take any x-value and multiply it by 2, you will get the corresponding y-value:
- 0 × 2 = 1,
- 1 × 2 = 3,
- 2 × 2 = 5,
- so on.
This pattern suggests a linear relationship between the x and y coordinates, which can be described by the equation y = 2x + 1.
This is called the slope-intercept form of the equation, where the slope (m) is 2 (indicating that for each 1-unit increase in x, y increases by 2), and the y-intercept is 1 (since the line crosses the y-axis at the point (0, 1)).
There are several other forms of the equation of a straight line, each useful depending on the information available:
- Slope-Intercept Form
- Point-Slope Form
- Standard Form
- Two-Point Form
- Intercept Form
- Normal Form
Note: The equation of line will always be a linear equation.
The equation of a straight line can be represented in several forms, each providing unique insights into the line's properties. Each form offers different insights, such as slope, intercepts, or specific points on the line, and is useful depending on the available data and problem context.
In the slope-intercept form, m represents the slope of the line, which indicates how steep the line is. c is the y-intercept, the point where the line crosses the y-axis. This form is particularly useful for quickly understanding the line’s slope and where it intersects the y-axis.
y = mx + c

Example: For the equation y = 2x + 3 the slope m is 2, and the y-intercept c is 3.
Characteristics:
- Slope (m): Indicates the steepness and direction of the line. Positive m means the line rises as x increases, while negative m means it falls.
- Y-intercept (c): The point where the line crosses the y-axis (x = 0).
- Ease of Graphing: This form is particularly useful for graphing because you can quickly plot the y-intercept and use the slope to determine the direction of the line.
The point-slope form is used when you know a specific point (x1, y1) on the line and the slope m. It’s helpful for writing the equation of a line when you have the slope and a single point on the line.
y - y1 = m(x - x1)

Example: If the line passes through the point (2, 3) with a slope of 4, the equation is y - 3 = 4(x - 2).
Characteristics:
- Point (x1, y1): Represents a specific point through which the line passes.
- Slope (m): Shows the steepness and direction of the line.
- Flexibility: Ideal for writing the equation when the slope and a single point on the line are known.
- Graphing: Requires knowing a specific point and slope but allows quick graphing once the point is plotted.
In the standard form, A, B, and C are integers, and the equation is typically written in a way where A and B are positive integers. This form is useful for solving systems of linear equations and is convenient for certain algebraic manipulations.
Ax + By + C = 0
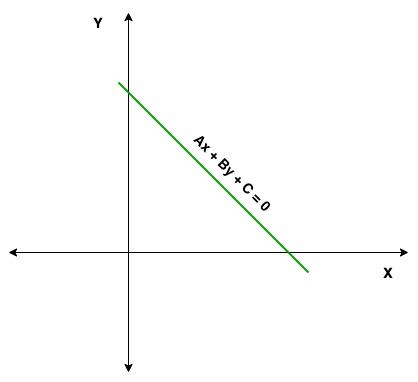
Example: The equation 3x + 4y = 12 is in standard form, where A = 3, B = 4, and C = 12.
Characteristics:
- Integer Coefficients (A, B): Typically written with integers, making it easy to work with in certain algebraic manipulations.
- Intercepts: The x-intercept can be found by setting y = 0, and the y-intercept can be found by setting x = 0.
- Solving Systems: Useful for solving systems of linear equations by addition or subtraction methods.
The two point form is used when you have two distinct points (x1, y1) and (x2, y2) on the line. It directly uses these points to derive the equation of the line.
\frac{y - y_1}{y_2 - y_1} = \frac{x-x_1}{x_2 - x_1}
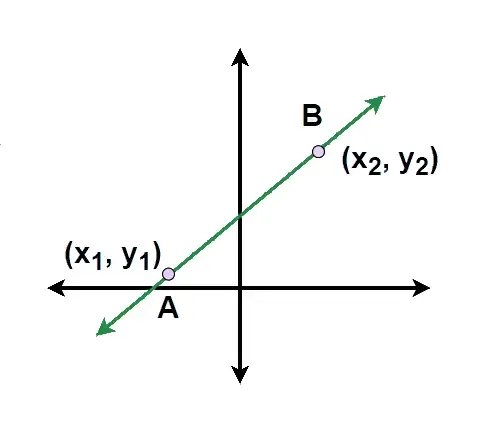
Example: For points (1, 2)and (4, 5), the equation can be derived as \frac{y - 2}{5 - 2} = \frac{x - 1}{4 - 1}.
Characteristics:
- Two Points (x1, y1) and (x2, y2): Uses two distinct points on the line to define it.
- Direct Calculation: Useful when only two points on the line are known.
- Graphing: This can be directly used to plot the line once the two points are identified
In the intercept form, a and b represent the x-intercept and y-intercept of the line, respectively. It’s useful when the intercepts are known or easy to determine.
\frac{x}{a} + \frac{y}{b} = 1

Example: If a line intercepts the x-axis at 4 and the y-axis at 3, its equation is \frac{x}{4} + \frac{y}{3} = 1
Characteristics:
- Intercepts (a and b): Represent the x-intercept (a) and y-intercept (b) directly.
- Simple Graphing: Easy to graph by plotting intercepts and drawing the line through them.
- Applications: Useful when intercepts are known or easily calculated.
The normal form uses θ to denote the angle of the line with the x-axis and p to represent the perpendicular distance from the origin. This form is useful in trigonometric applications.
x cos θ + y sin θ = p

Example: The equation xcos(45∘) + ysin(45∘) = 5 is in normal form, where:
- p = 5 (the perpendicular distance from the origin),
- θ = 45∘(the angle the line makes with the positive x-axis).
Characteristics:
- Angle (θ): The angle between the line and the x-axis, indicating the direction of the normal (perpendicular) to the line.
- Distance (p): The perpendicular distance from the origin to the line.
- Applications: Often used in geometric and trigonometric contexts for problems involving distances and angles.
Below is the table with the form name along with its equation and description:
| Form Name | Equation | Description |
|---|
| Point-Slope Form | (y - y1) = m(x - x1) | It represents a line using the slope (m) and a point on the line (x1, y1). |
| Slope-Intercept Form | y = mx + b | It represents a line using the slope (m) and the y-intercept (b). |
General Form | ax + by + c = 0 | It represents a line using one point(x, y) and some constants ( a, b, c ) |
| Intercept Form | x/a + y/b = 1 | It represents a line where it intersects the x-axis at (a, 0) and the y-axis at (0, b). |
| Normal Form | x cos θ + y sin θ = p | It represents a line using the angle (θ) the line makes with the positive x-axis and the perpendicular distance (p) from the origin to the line. |
Derivation of the Equation of a Straight Line
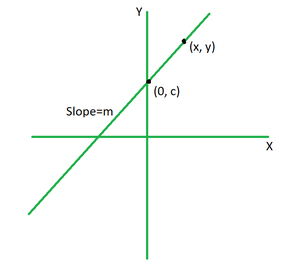
Consider two points on the above line (x1, y1) = (0, c) and (x2, y2) = (x, y).
The slope of the line is given by,
m=\frac{y_2-y_1}{x_2-x_1}
m=\frac{y-c}{x-0}
mx = y – c
y = mx + c
This is the general equation for a straight line, which includes its slope and y-intercept. As a result, the equation of line formula is derived.
Example: Find the equation of a line with slope 2 and y-intercept 4.
We have, m = 2 and c = 4
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = 2x + 4
Solved Examples of Equations of a Straight Line
Example 1. Find the equation of a line with slope –5 and y-intercept 1.
Solution:
We have, m = –5 and c = 1
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = –5x + 1
Example 2. Find the equation of a line with slope 7 and y-intercept 9.
Solution:
We have, m = 7 and c = 9
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = 7x + 9
Example 5. Find the equation of a line with slope 2 and y-intercept –3.
Solution:
We have, m = 2 and c = –3
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = 2x + (–3)
y = 2x – 3
Example 6. Find the equation of a line with slope 4 and y-intercept –1.
Solution:
We have, m = 4 and c = –1
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = 4x – 1
Example 3. Find the equation of a line with slope 1/2 and y-intercept 4.
Solution:
We have, m = 1/2 and c = 4
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = (1/2)x + 4
y = x/2 + 4
2y = x + 8
Example 4. Find the equation of a line with slope –10 and y-intercept 1/4.
Solution:
We have, m = –10 and c = 1/4
The equation of a line is given by slope-intercept form, that is, y = mx + c.
So, the required equation is,
y = –10x + 1/4
4y = –40x + 1
Also Read:
Unsolved Practice Questions on Equation of Straight Line
Question 1: Find the equation of the line that has a slope of 3 and a y-intercept of -5.
Question 2: Determine the slope and y-intercept of the line given by the equation y = −2x + 7.
Question 3: Write the equation of the line that passes through the point (2, -3) with a slope of 4.
Question 4: Convert the equation 2x − 3y = 6 into the slope-intercept form and find the slope and y-intercept.
Question 5: Determine the slope and y-intercept of the line given by the equation 5x − 7y + 2 = 0.
Question 6: Find the equation of the line passing through the points (1, 2) and (4, 5) using the two-point form.
Question 7: Write the equation of a line that has an x-intercept of 4 and a y-intercept of -3 using the intercept form.
Question 8: Write the equation of the line in a point-slope form that passes through (3, -2) and is parallel to the line y = 12x + 1.
Question 9: Convert the line equation 4x + 6y = 24 into the intercept form and identify the x-intercept and y-intercept.
Question 10: For a line that makes an angle of 30 degrees with the positive x-axis and has a perpendicular distance of 6 units from the origin, find the equation using the normal form.
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice