Heron's formula is a popular method for calculating the area of a triangle when the lengths of its three sides are known. It was introduced by Heron of Alexandria in his book "Metrica". This formula applies to all types of triangles, including right-angled, equilateral, and isosceles.
According to this formula, the area of a triangle is directly proportional to the square root of the semi-perimeter of the triangle. The area "A" of a triangle with sides of lengths a, b, and c is given by:
A = \sqrt{s(s - a)(s - b)(s - c)}
Where,
- A is area of Triangle ABC,
- a, b, c are lengths of the sides of the triangle, and
- s is semi-perimeter = (a + b + c)/2.
Below is the demonstration of Heorn's Formula for finding the area of the triangle with sides of length a, b, c:
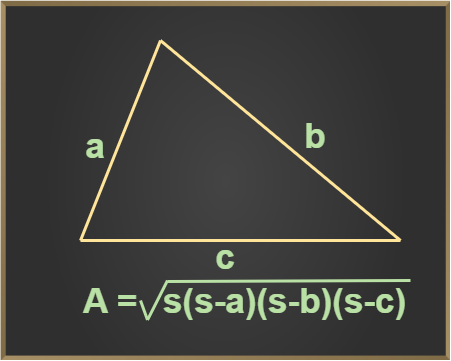 Heron's Formula
Heron's Formula
History of Heron's Formula
In 60 CE, Heron of Alexandria gave a formula which is known as the Heron's Formula. Heron was a Greek Mathematician who gave the formula for finding the area of a triangle when the length of all sides of the triangle is given. He used this formula for solving various problems in triangles and trigonometry. He proved the Law of Cosine and the Law of Cotangent using this formula.
There are two primary methods to derive Heron’s formula: using the Pythagorean Theorem or the Cosine Rule.
To begin the derivation, recall that the area of a triangle can be expressed as:
Area of a Triangle = (1/2) × b × h
Where,
- b is the base, and
- h is the height.
The image shown below shows the triangle ABC.
Start by breaking the triangle into two smaller right-angled triangles and applying the Pythagorean Theorem to each, we can solve for the area in terms of the sides a, b, and c.
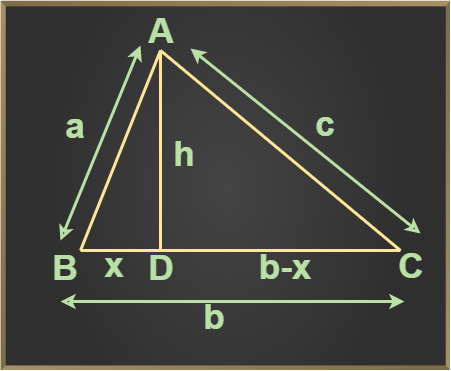 Heron's Formula Using Pythagoras Theorem
Heron's Formula Using Pythagoras Theorem
Draw a perpendicular AD on BC
From the ∆ ABD,
a2 = x2 + h2
⇒ x2 = (a2 − h2)....(I)
⇒ x = √(a2 − h2)....(ii)
Consider the ∆ACD,
(b − x)2 + h2 = c2
⇒ (b − x)2 = c2 − h2
⇒ b2 − 2bx + x2 = c2 – h2
Putting the value of x and x2 from equations (i) and (ii) in the above equation, we get
b2 – 2b√(a2 − h2)+ a2 − h2 = c2 − h2
⇒ b2 + a2 − c2 = 2b√(a2 − h2)
Squaring on both sides, we get;
(b2 + a2 – c2)2 = 4b2(a2 − h2)
⇒ {(b2 + a2 – c2)2) / 4b2 = (a2 − h2)
⇒ a2 + {(b2 + a2 – c2)2) / 4b2 = h2
Simplifying, we get
h2 = (a + b + c)(b + c - a)(a + c - b)(a + b - c) / 4b2
Now, 2s = a + b + c, where s is the semi-perimeter of the triangle.
h2 = 2s(2s - 2a)(2s - 2b)(2s - 2c) / 4b2
⇒ h = √[2s(2s - 2a)(2s - 2b)(2s - 2c)] / 2b
⇒ h = 2 × √[s(s - a)(s - b)(s - c)] / b...(iii)
From, area of triangle = 1/2 × b × h
Now, area of triangle = 1/2 × {b × 2 × √[s(s - a)(s - b)(s - c)]} / b, cancelling out the similar terms we get:
Area of Triangle (A) = \sqrt{s(s-a)(s-b)(s-c)}
Heron's Formula can also be easily solved using the Cosine Rule. Now for any triangle ABC if the sides of the triangle are a, b, and c and their opposite angles are, α, β, and γ.
The law of cosine states, cos γ = (a2 + b2 - c2)/2ab
Using Trigonometric identites
cos2 γ + sin2 γ = 1
⇒ sin γ = √(1 - cos2 γ)
⇒ sin γ = √[1 - {(a2 + b2 - c2)/2ab}2]
⇒ sin γ = √[(4a2b2 - (a2 + b2 + c2)2]/2ab
If the base of the triangle is a then its altitude is b sin γ
Area of Triangle = 1/2 base × height
⇒ Area of Triangle = 1/2 × a × b sin γ
⇒ Area of Triangle = 1/2 ab × √[(4a2b2 - (a2 + b2 + c2)2]/2ab
⇒ Area of Triangle = 1/4 √[c2 - (a - b)2][(a + b)2 - c2]
⇒ Area of Triangle = √(b + c - a)(a + c - b)(a + b - c)(a + b + c)/16
Area of Triangle = √s(s - a)(s - a)(s - b)
Where s = (a + b + c)/2 is the semi perimeter.
For an equilateral triangle, all sides are equal. Now, the semi-perimeter of the equilateral triangle is (s) = (a + a + a) / 2
⇒ s = 3a / 2
where a is the length of the side.
Now, using Heron’s Formula,
Area of Equilateral Triangle = √(s(s – a)(s – a)(s – a), upon multiplication, the formula becomes:
Area of Equilateral Triangle = √3 / 4 × a2
Isosceles Triangle is a triangle that has two equal sides, their area can be easily calculated using Heron's Formula. For any isosceles triangle △ABC where sides AB = a, and BC = a are equal, and the third side is CA = b. The formula for its area is,
Area of iscosceles triangle ABC(A) = √s(s - a)(s - a)(s - b)
Where s is the semi-perimeter i.e., s = (a + a + c)/2.
⇒ s = (a + a + b)/2
⇒ s = (2a + b)/2
Simplifying, A = √s(s - a)(s - a)(s - b)
Substituting "s" = (2a + b)/2:
⇒ s − a = (2a + b)/2 − a = b/2
⇒ s − b = (2a + b)/2 − b = (2a − b)/2
Thus: a =\sqrt{(\frac{2a + b}{2})(\frac{b}{2})(\frac{b}{2})(\frac{2a - b}{2})}
Simplyfy further: A = \sqrt{\frac{(2a+b)(2a-b)(b^2)}{2} }
A = 1/4√(4a2 - b2)(b2)
Final Formula:
A = \frac{b}{2}\sqrt{a^2 - \frac{b^2}{4}}
Note: Heron's formula for a Scalene triangle remains the same as the default formula, as it applies to all types of triangles, including scalene, isosceles, and equilateral, provided the lengths of the three sides are known.
Heron's Formula for Area of Quadrilateral
Heron's formula is used to determine the formula for the area of the quadrilateral. We can divide the quadrilateral into two separate triangles using any one of its diagonals and then the area of the two separate triangles is calculated using Heron's Formula.
The area of the quad ABCD is calculated by dividing it into two triangles using its diagonal. Let's say we join the vertices A and C to form the diagonal AC then we divide it into two triangles △ABC and △ADC. If we take the length of sides of the quadrilateral as,
AB = b, BC = c, CD = d, and DA = a, and the length of diagonal AC is e then its area is calculated using,
 Heron's Formula for the Area of Quadrilateral
Heron's Formula for the Area of Quadrilateral
Area of quad ABCD = Area of △ABC + Area of △ADC...(i)
Area of triangle ABC
Area of △ ABC = √(s1(s1 - b)(s1 - c)(s1 - e))
Where s1 = (b + c + e)/2.
Area of triangle ADC
Area of △ ADC = √(s2(s2 - d)(s2 - a)(s2 - e))
Where s2 = (d + a + e)/2.
Thus,
form eq(i)
Area of quad ABCD = √(s1(s1 - b)(s1 - c)(s1 - e)) + √(s2(s2 - d)(s2 - a)(s2 - e))
Where,
- s1 = (a + b + e)/2, and
- s2 = (a + d + e)/2
Heron's formula has various applications and some of the important applications of Heron's Formula are,
- For finding the area of the triangle if the sides of the triangle are given
- For finding the area of the quadrilateral the length of all the sides and the length of the diagonal are given.
- For finding the area of any polygon its sides and the length of all the principal diagonals are given.
Read in Detail: Applications of Heron’s Formula
Example 1: Calculate the area of a triangle whose lengths of sides a, b, and c are 14cm,13cm, and 15 cm respectively.
Solution:
Given:
a = 14cm
b = 13cm
c = 15cm
Firstly, we will determine semi-perimeter(s) s = (a + b + c)/2
⇒ s = (14 + 13 + 15)/2
⇒ s = 21 cm
Thus, A = √(s(s – a)(s – a)(s – a)
⇒ A = √(21(21 – 14)(21 – 13)(21 – 15)
⇒ A = 84 cm2
Example 2: Find the area of the triangle if the length of two sides is 11cm and 13cm and the perimeter is 32cm.
Solution:
Let a, b and c be the three sides of the triangle.
a = 11cm
b= 13 cm
c = ?
Perimeter = 32cm
As we know, Perimeter equals to the sum of the length of three sides of a triangle.
Perimeter = (a + b + c)
⇒ 32 = 11 + 13 + c
⇒ c = 32 - 24
⇒ c = 8 cm
Now as we already know the value of perimeter,
s = perimeter / 2
⇒ s = 32 / 2
⇒ s =16 cm
As, a = 11cm, b = 13 cm, c = 8 cm, s = 16 cm
Thus, A = √(s(s – a)(s – a)(s – a)
⇒ A = √(16(16 – 11)(16 – 13)(16 – 8)
⇒ A = 43.8 cm2
Example 3: Find the area of an equilateral triangle with a side of 8 cm.
Solution:
Given,
Side = 8 cm
Area of Equilateral Triangle = √3 / 4 × a2
⇒ Area of Equilateral Triangle = √3 / 4 × (8)2
⇒ Area of Equilateral Triangle = 16 √3 cm2
Practice Questions: Heron's Formula Questions with solutions.
Related Reads
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice