Law of Total Probability

In probability theory, an event is any outcome or set of outcomes from a random experiment, and the probability of an event is a number that represents the likelihood of that event occurring.

The Law of Total Probability is a fundamental rule in probability theory that allows you to compute the probability of an event based on a partition of the sample space. The idea is that if an event can occur in several ways, the total probability of the event is the sum of the probabilities of the different ways in which it can occur.

Understanding the Law of Total Probability

The Law of Total Probability states that if A₁, A₂, ..., A_n are mutually exclusive and exhaustive events (meaning they cover all possible outcomes and do not overlap, Ai ∩ Aj= NULL for i ≠ j), and B is an event of interest, then the probability of B can be calculated as:

P(B) = \sum_{i=1}^n P(B∣A_i)P(A_i)

A fundamental rule in the theory of probability that is interconnected to marginal probability and conditional probability is called the law of total probability, the total probability theorem, o law of alternatives.

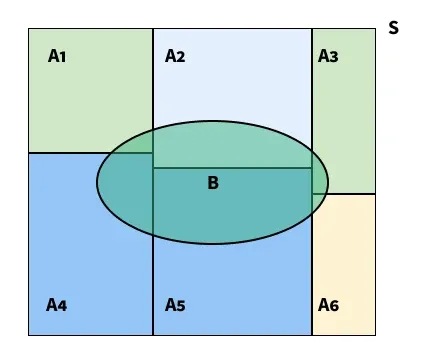
The theorem of total probability is the core foundation of Baye's theorem. In this article, we have discussed important concepts related to total probability.

Total Probability Theorem Proof

Let A_1, A_2, \dots, A_k be disjoint events forming a partition of the sample space E (i.e., A_1 \cup A_2 \cup \dots \cup A_k = E ) with P(A_i) > 0 for all i. For any event B:

Partition B using A_i:

Since \bigcup_{i=1}^k A_i = E , we can write:
B = B \cap E = B \cap \left( \bigcup_{i=1}^k A_i \right).

Distributive Property: Intersection distributes over union:
B = \bigcup_{i=1}^k (B \cap A_i)

Disjointness of B \cap A_i:
Because A_i are disjoint, (B \cap A_i) and (B \cap A_j) are also disjoint for i \neq j. Thus:
P(B) = P\left( \bigcup_{i=1}^k (B \cap A_i) \right) = \sum_{i=1}^k P(B \cap A_i).

Conditional Probability: By definition of conditional probability:
P(B \cap A_i) = P(B \mid A_i) \cdot P(A_i).

Final Result:

Substituting into the previous equation:
P(B) = \sum_{i=1}^k P(B \mid A_i) \cdot P(A_i). \quad

Hence, the proof. so referred to as the total probability theorem or law of alternatives.

Note:

The law of total probability is used when you don't know the probability of an event, but you know its occurrence under several disjoint scenarios and the probability of each scenario.

Application of Theorem of Total Probability

Bayes' Theorem

• It is used for the evaluation of the denominator in Bayes' theorem. Bayes’ Theorem for n set of events is defined as,
• Let E₁, E₂,…, E_n be a set of events associated with the sample space S, in which all the events E₁, E₂,…, E_n have a non-zero probability of occurrence. All the events E₁, E₂,…, E form a partition of S. Let A be an event from space S for which we have to find probability, then according to Bayes’ theorem,

P(E_i \mid A) = \frac{P(E_i) \cdot P(A \mid E_i)}{\sum_{k=1}^n P(E_k) \cdot P(A \mid E_k)}

• Used in spam detection, classification, sentiment analysis.

Expectation-Maximization (EM) Algorithm

• It is used in estimating latent (hidden) variables in probabilistic models (e.g., GMMs).
• Law of Total Probability is used in computing the E-step - expected value of latent variables using:
  P(Z|X,θ) = \frac{P(X|Z,θ)P(Z| θ)}{P(X|θ)}
  where P(X∣θ) is computed using the Law of Total Probability: P(X∣θ)=∑P(X∣Z,θ)P(Z∣θ)
• Used in clustering in Gaussian Mixture Models (GMMs).

Hidden Markov Models (HMMs)

• Law of Large numbers is used in computing the probability of observed sequences when states are hidden.
• The Forward-Backward Algorithm computes: P(X)=∑_{hidden\: states\: Z}P(X∣Z)P(Z)
• Used in speech recognition, POS tagging, gene prediction.

Bayesian Networks & Marginalization

• Law of total probability is used in inferring probabilities in directed graphical models.
• To compute marginal probabilities, we sum over all possible values of other variables: P(X)=∑_{Y,Z}P(X,Y,Z)
• Used in medical diagnosis (Given symptoms, compute the probability of a disease by marginalizing over unknown factors.), sensor networks, and decision-making systems.

Solved Examples on Law of Total Probability

1. We draw two cards from a deck of shuffled cards with replacements. Find the probability of getting the second card a king.

Solution:

Let, A - represent the event of getting the first card a king. B - represent the event that the first card is not a king. E - represents the event that the second card is a king. Then the probability that the second card will be a king or not will be represented by the law of total probability as:

P(E)= P(A)P(E|A) + P(B)P(E|B)

Where, P(E) is the probability that the second card is a king, P(A) is the probability that the first card is a king, P(E|A) is the probability that the second card is a king given that first card is a king, P(B) is the probability that the first card is not a king, P(E|B) is the probability that the second card is a king but the first card drawn is not a king. According to the question:

P(A) = 4 / 52 P(E|A) = 4 / 52 P(B) = 48 / 52 P(E|B) = 4 / 52

Therefore,

P(E) = P(A)P(E|A) + P(B)P(E|B) =(4 / 52) * (4 / 52) + (48 / 52) * (4 / 52) = 0.0769230

2. A factory produces three types of products: P₁, P₂, and P₃. The production of P₁, P₂, and P₃ is 30%, 20%, and 50% of the total production, respectively. The probability that a product is defective is 1% for P₁, 2% for P₂, and 3% for P₃. If a product is selected at random, what is the probability that it is defective?

Solution:

Let A₁, A₂, and A₃ represent the events of producing P₁, P₂, and P₃, respectively. Let D represent the event that the product is defective.

P(A₁) = 0.30 P(A₂) = 0.20 P(A₃) = 0.50 P(D∣A₁) = 0.01 P(D∣A₂) = 0.02 P(D∣A₃) = 0.03

Using the Law of Total Probability:

P(D) = P(D∣A₁)P(A₁) + P(D∣A₂)P(A₂) + P(D∣A₃)P(A₃) P(D) = (0.01×0.30) + (0.02×0.20) + (0.03×0.50)
P(D) = 0.003 + 0.004 + 0.015 = 0.022

3. A driver passes through two traffic lights on his way to work. The probability that the first light is green is 0.3, and the probability that the second light is green given that the first light is green is 0.6. The probability that the second light is green given that the first light is not green is 0.2. What is the probability that the driver sees a green light at the second intersection?

Solution:

Let G1 represent the event that the first light is green and G2 represent the event that the second light is green.

P(G₁) = 0.3 P(G₁') = 0.7 P(G₂∣G₁) = 0.6 P(G₂∣G₁') = 0.2

Using the Law of Total Probability:

P(G₂) = P(G₂∣G₁)P(G₁) + P(G₂∣G₁')P(G₁') P(G₂) = (0.6×0.3) + (0.2×0.7)
P(G₂) = 0.18+0.14 = 0.32

4. In a town, 60% of the population supports Candidate X, while 40% supports Candidate Y. A survey is conducted where 70% of Candidate X's supporters and 20% of Candidate Y's supporters favor a particular policy. What is the probability that a randomly selected person from the town favors this policy?

Solution:

Let X represent the event that a person supports Candidate X and Y represent the event that a person supports Candidate Y. Let P represent the event that a person favors the policy.

P(X) = 0.6 P(Y) = 0.4 P(P∣X) = 0.7 P(P∣Y) = 0.2

Using the Law of Total Probability:

P(P) = P(P∣X)P(X) + P(P∣Y)P(Y) P(P) = (0.7×0.6) + (0.2×0.4) P(P) = 0.42 + 0.08 = 0.50

5. A meteorologist predicts that there is a 30% chance of rain tomorrow. If it rains, there is a 60% chance that it will be a storm. If it doesn't rain, there is a 5% chance of a storm due to other factors. What is the probability that there will be a storm tomorrow?

Solution:

Let R represent the event of rain, and S represent the event of a storm.

P(R) = 0.3 P(R') = 0.7 P(S∣R) = 0.6 P(S∣R') = 0.05

Using the Law of Total Probability:

P(S) = P(S∣R)P(R) + P(S∣R')P(R') P(S) = (0.6 × 0.3) + (0.05 × 0.7) P(S) = 0.18 + 0.035 = 0.215

Also Read:

• Probability with Solved Examples
• Probability Theory
• How to Calculate Probability
• Probability Theorems

Conclusion

The Law of Total Probability is a fundamental principle in probability theory used for determining the probability of an event by considering all possible scenarios in which it might occur. This theorem is related to marginal and conditional probabilities, and provides foundation for Bayes' Theorem. It is useful when the direct probability of an event is unknown, but its probability under various conditions is known. The theorem is essential for various applications.

Practice Problems on Law of Total Probability

1. A certain disease affects 0.1% of the population. A medical test for this disease is 99% accurate. What is the probability that a randomly selected person who tests positive actually has the disease?

2. A shipment contains three different components: A, B, and C. The probabilities of selecting a A, B, and C component are 0.4, 0.35, and 0.25, respectively. The probabilities that a selected component is defective are 0.02 for A, 0.03 for B, and 0.05 for C. What is the probability that a randomly selected component from the shipment is defective?

3. In a certain population, 1% of people have Disease A. A test for Disease A is 95% accurate. What is the probability that a person has Disease A given that they tested positive?

4. In a certain town, it is known that 40% of the population prefer tea, 30% prefer coffee, and the 30% prefer juice. If a person is chosen at random, the probability that they are satisfied with their choice of beverage is 0.7 for tea drinkers, 0.8 for coffee drinkers, and 0.6 for juice drinkers. What is the probability that a randomly chosen person is satisfied with their choice of beverage?

5. In a school, 70% of the students are in the science stream, and 30% are in the arts stream. The pass rate is 85% for science students and 75% for arts students. If a randomly selected student passes, what is the probability that they are in the science stream?

6. You are given three boxes. The first box contains 2 red and 1 white ball, the second contains 1 red and 2 white balls, and the third contains 3 red and 1 white ball. A box is chosen at random and a ball is drawn. If the ball is red, what is the probability that it was drawn from the third box?

7. A traffic light is green 50% of the time, yellow 10% of the time, and red 40% of the time. If you approach the light and it is not red, what is the probability that it is green?

8. There are three factories producing the same product. Factory A produces 40% of the products, Factory B produces 35%, and Factory C produces 25%. The probability of a defective product from these factories is 2%, 3%, and 5% respectively. If a product is found to be defective, what is the probability it was produced by Factory B?

9. A disease test has a false positive rate of 5% and a false negative rate of 2%. In a population where 2% of people have the disease, what is the probability that a person who tests positive actually has the disease?

10. A factory has two suppliers A and B. A supplies 60% of the components and B supplies 40%. The defect rates for these suppliers are 1% and 2% respectively. If a component is found to be defective, what is the probability that it was supplied by B?

Answers:

1. 9.02%
2. 3.1%
3. 16.1%
4. 70%
5. 72.56%
6. 3773​ (≈ 42.86%)
7. 5665​ (≈ 83.33%)
8. 33.87%
9. 28.57%
10. 57.14%

Related Articles:

• Probability Distribution – Function, Formula, Table
• Bayes’ Theorem
• Conditional Probability