Pentagon in Maths | Shape, Parts, Types, Examples
Last Updated :
23 Jul, 2025
The pentagon is a two-dimensional polygon with five straight sides and five interior angles. There are two main types of pentagons:
- Regular Pentagon: When all sides and angles are equal, it is called a regular pentagon. In a regular pentagon, each interior angle measures 108°, and the sum of all interior angles is always 540°.
- Irregular Pentagon: If the sides and angles are not equal, the pentagon is classified as an irregular pentagon.
Below is the figure of a regular Pentagon with sides s:
 A Regular Pentagon
A Regular PentagonNote: The term "Pentagon" originates from the Greek words "Penta," which means "five," and "gonia," which means "angles." Thus, a Pentagon is a geometric figure defined by having five sides and five interior angles.
In the case of a regular pentagon, all five sides are equal in length, all five interior angles measure 108 degrees, and the shape possesses both reflectional and rotational symmetry about its center, resulting in five lines of symmetry.
Parts of Pentagon
The parts of a pentagon are shown in the image below:
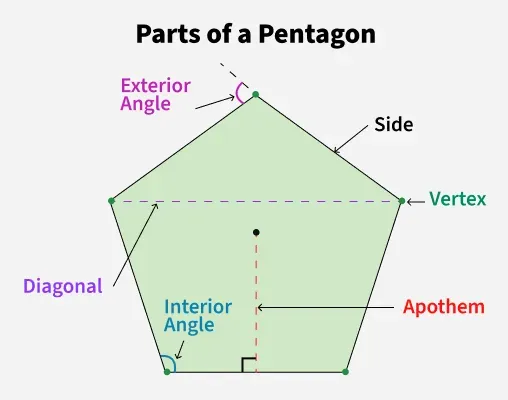 Detailed diagram of a regular pentagon
Detailed diagram of a regular pentagonLet's learn about these parts in detail:
| Term | Definition |
|---|
| Side | One of the five line segments that together form the boundary of a pentagon. |
| Vertex | A point where two sides of the shape meet. It's also referred to as a corner. |
| Diagonal | A line segment connecting two non-adjacent vertices of the polygon. |
| Exterior Angle | The angle between one side of the polygon and the extension of an adjacent side. |
| Interior Angle | The angle formed inside the polygon between two adjacent sides. |
| Apothem | A line from the center of the polygon perpendicular to one of its sides. It also represents the shortest distance from the center to the side. |
Types of Pentagons
Pentagons can be classified into four types depending on their sides, angles, and vertices.
- Based on the Length of the Side: Regular Pentagon, Irregular Pentagon.
- Based on the Measure of Angle: Convex Pentagon, Concave Pentagon.
- Other types: Equilateral Pentagon, Cyclic Pentagon.
Let's discuss them in detail.
Regular and Irregular Pentagons
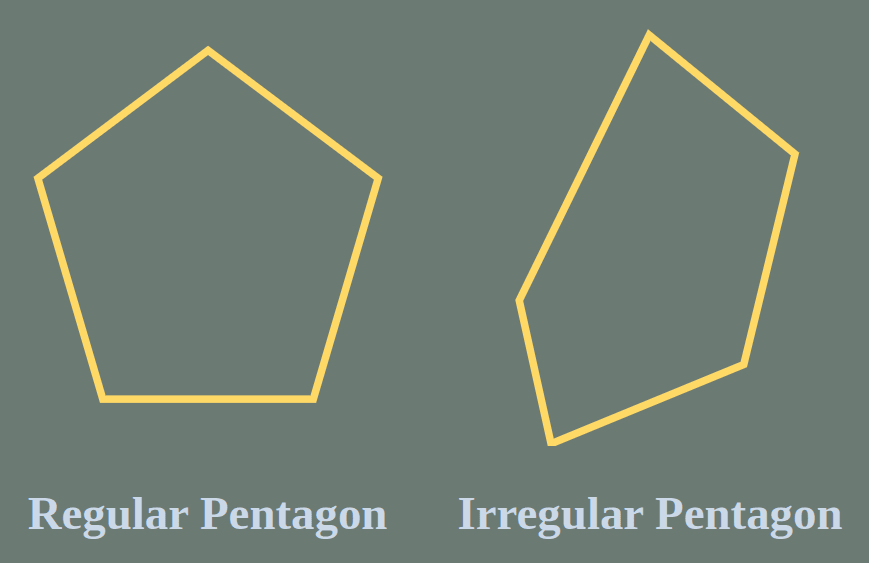
- A regular pentagon has all its sides of equal length, and all its angles have the same measure. This symmetry ensures that the polygon looks the same from any angle or side. In the case of a regular pentagon, it always appears identical.
- An irregular pentagon lacks this symmetry because it has varying side lengths and angles. As a result, the shape may look different when observed from different angles or sides.
Convex and Concave Pentagon
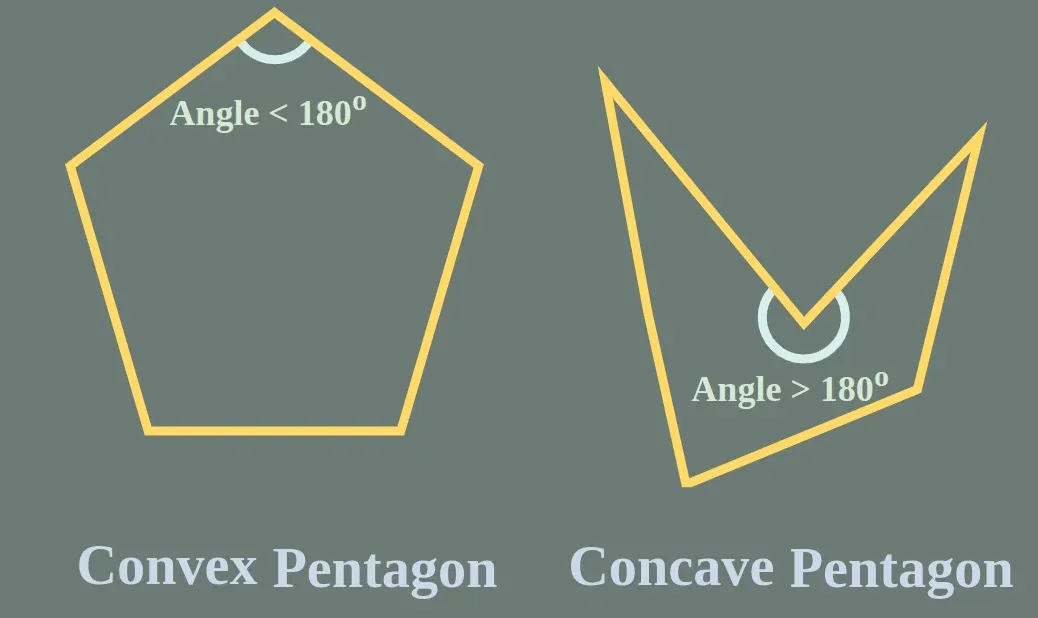
- A convex pentagon is a polygon in which all its vertices point outward, creating a shape that does not point inward. In a convex pentagon, no internal angle is greater than 180°.
- A concave pentagon has a bowl-like structure between some sides and at least one vertex that points inward. In a concave pentagon, at least one internal angle is greater than 180°.
Equilateral Pentagon
An Equilateral Pentagon is a geometric shape where all five sides are of the same length. While the angles within this type of pentagon can vary within a specific range, it is referred to as "equilateral and equiangular" when all sides and angles are equal.
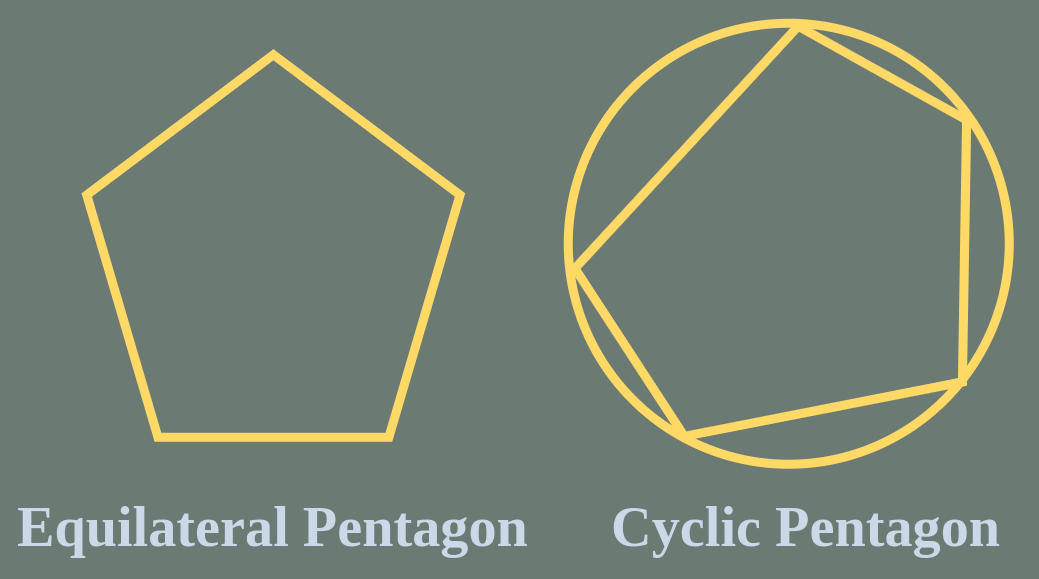
Cyclic Pentagon
A Cyclic Pentagon is a polygon in geometry where all of its vertices are positioned on the circumference of a circle. This characteristic of having its vertices on the circle's boundary is what defines it as a "cyclic" pentagon. A classic example of a cyclic pentagon is a regular pentagon.
Angles in a Pentagon
An angle is created when two sides of the Pentagon intersect at a common point called the Vertex. A pentagon has two types of angles.
- Interior Angle
- Exterior Angle
Let's discuss both these angles in detail.
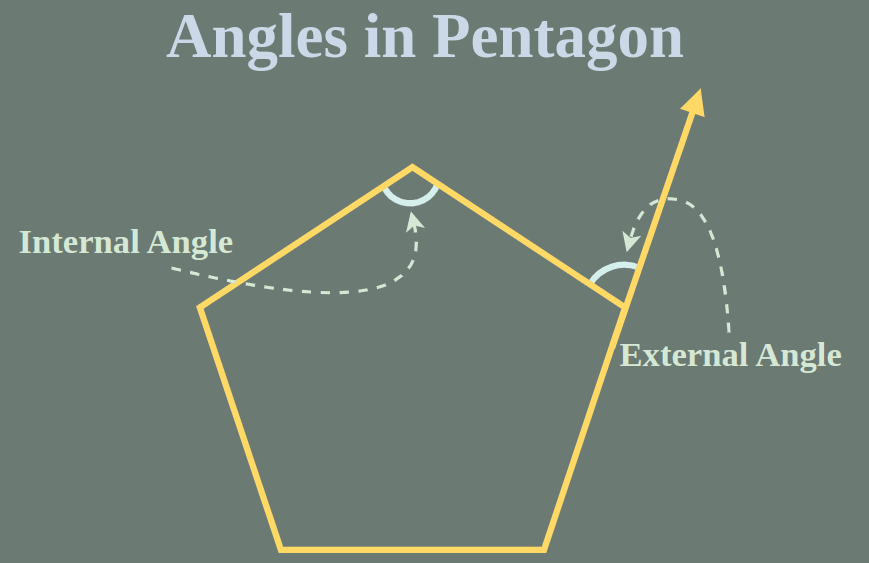
Interior Angle of a Pentagon
An Interior Angle is the angle formed by two adjacent sides of the shape on the inside. When two straight lines intersect within the shape, they create Interior Angles.
Sum of Interior Angle of Pentagon = 540°
A Pentagon can be thought of as composed of three triangles. Therefore, the Total Sum of Angles in a Pentagon is equivalent to the sum of angles in three triangles, which is 3 times the sum of angles in one triangle (180 degrees). This results in a sum of 540 degrees for the Interior Angles of a Pentagon.
Sum of Interior Angles in any Polygon = 180° × (n − 2)
Where 'n' represents the number of sides. In the case of a Pentagon with 5 sides, this formula will be:
Sum of Interior Angles of a Pentagon = 180° × (5 − 2) = 3 × 180° = 540°.
Note: Each Interior Angle of a Regular Pentagon is equal to 540° ÷ n = 540° ÷ 5 = 108°.
Exterior Angle of a Pentagon
An Exterior Angle is the angle formed by two adjacent sides of the shape on the outside. It measures the angle at a specific vertex, but on the exterior of the shape.
Sum of Exterior Angles of a Pentagon = 360°.
To prove that the sum of exterior angles of a polygon is 360°, we can follow these steps:
We know the formula for the sum of interior angles of a regular polygon with 'n' sides, which is 180° × (n − 2).
Each interior angle in the polygon can be calculated as: 180° × (n-2)/n .
It's a known fact that each exterior angle in a polygon is supplementary to its corresponding interior angle.
So, Each exterior angle can be expressed as: [180°n - 180°n + 360°]/n, which simplifies to 360°/n.
To find the Total Sum of Exterior Angles for the polygon, we multiply the number of sides 'n' by the measure of each exterior angle (360°/n).
Applying this to a pentagon with 5 sides (n = 5), we observe that the sum of exterior angles for the pentagon is 5 x (360°/5) = 360°
Note: Each exterior angle of a regular pentagon is equal to 360° ÷ n = 360° ÷ 5 = 72°.
Real-Life Examples of Pentagon
- A diamond can resemble a pentagon with its five sides and five corners.
- The headquarters of the United States Department of Defense is famously known as the Pentagon due to its architectural resemblance to a pentagon shape.
- A football is constructed from several black and white pentagonal patches of five-sided shape.
- Echinoderms like sea stars exhibit a pentagonal symmetry in their body structure.

Properties of Pentagon
A Pentagon is a 2D shape featuring five sides and five interior angles. Its key properties include:
The sum of the interior angles in a Pentagon is always 540°.
For a Regular Pentagon:
- All five sides are of equal length.
- All interior angles are congruent, measuring 108° each.
- All exterior angles are also congruent, with a measurement of 72°.
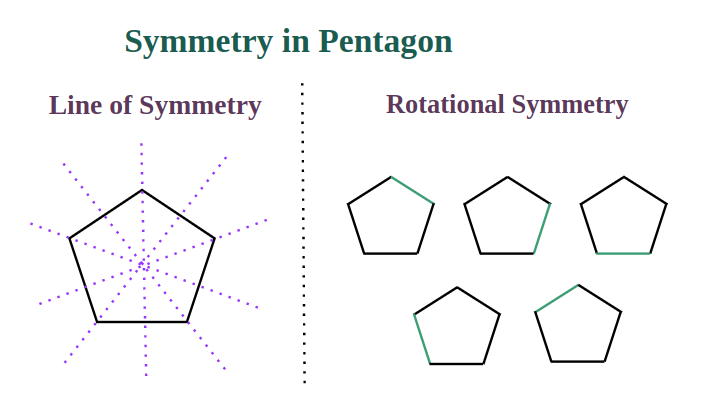
- Regular pentagons have five lines of symmetry, dividing the shape into congruent parts.
- They also possess five rotational symmetries.
- Five diagonals intersect at a common point within the pentagon.
- The ratio of the diagonal's length to the side's length in a regular pentagon is the golden ratio, (1 + √5)/2.
Line of Symmetry
The number of lines of symmetry in a regular polygon is equivalent to the number of its sides. These symmetrical lines extend from a vertex to the midpoint of the opposite side, creating a total of 5 lines that divide the pentagon into congruent halves. A regular pentagon has five lines of symmetry: one horizontal, one vertical, and three diagonals.
Formulas Related to the Pentagon
The following table shows the list of all the formulas necessary to calculate the various pentagon properties:
Property | Formula |
|---|
Perimeter | - For Regular Pentagon: 5(a).
- For Irregular Pentagon: The Sum of all the sides.
|
Area | - For Regular Pentagon: \frac{1}{4}\sqrt{5(5+2\sqrt{5}a^2)}
- If Apothem is given: ½ ⨉ P ⨉ a
- If only the radius is given: (\frac{5}{2})r^2 (sin \ 72\degree)
- If only the side length is given: \dfrac{5 s^2}{(4 \ \tan 36\degree)}
- For Irregular Pentagon: Divide the pentagon into smaller polygons, then calculate the area of each polygon and sum them up.
|
Diagonal | - Number of diagonals: \dfrac{n(n-3)}{2}
- Diagonal length: \dfrac{1+\sqrt{5}}{2} \ a
|
Side | - P/5 {where P is perimeter}
|
People Also Read:
Solved Examples of Pentagon
Example 1: Determine the area of a Regular Pentagon if it has a side length of 20 cm and an apothem of 15 cm.
Solution:
Given Data,
Side Length = 20 cm
Length of apothem = 15 cm
Area = ½ × perimeter × apothem.
In this case, the perimeter is 5 times the length of one side, which is 20 cm. So, the formula becomes:
Area = ½ × 5 × 20 × 15.
Solving this equation:
Area = ½ × 5 × 20 × 15 = ½ × 1500 = 750 square cm.
Hence, the area of the Regular Pentagon is 750 square cm.
Example 2: If the perimeter of a Regular Pentagon is 400 cm, find the length of each side.
Solution:
The perimeter of the Regular Pentagon is 400 cm.
The perimeter of a Regular Pentagon is equal to the product of the number of sides and the length of each side. In this case, there are 5 sides, so:
Perimeter = 5 × Side
Now, we can solve for the length of each side:
400 cm = 5 × Side
To find the length of each side, divide both sides of the equation by 5:
Side = 400 cm / 5 = 80 cm
So, the length of each side of the Regular Pentagon is 80 cm.
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice