Perimeter of a Parallelogram
Last Updated :
23 Jul, 2025
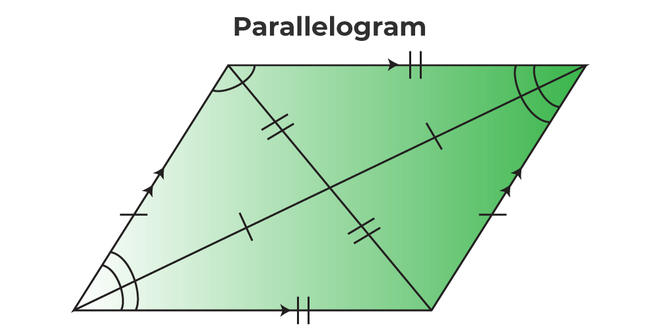
A parallelogram is a type of quadrilateral with four equal sides with opposite sides equal. Its sides do not intersect each other. There are two diagonals of a parallelogram that intersect each other at the center. A diagonal divides the parallelogram into two equal parts or triangles. The following are the properties of a parallelogram:
- A parallelogram has four sides.
- Opposite sides of parallelograms are equal and parallel.
- Opposite angles of parallelograms are equal.
- Diagonals of parallelograms intersect each other.
The perimeter of a parallelogram is the total length of its boundary, calculated as the sum of all its sides.
However, not every time the length of all the sides will be given to us, sometimes some other information regarding a parallelogram is given. Therefore, there are different formulas for the perimeter of a parallelogram.
Perimeter of Parallelogram Formulas
For a quadrilateral, perimeter refers to the sum of the length of the four sides. So, the perimeter of a parallelogram will be the sum of its four sides. The perimeter of a parallelogram can be calculated using three cases. The three cases are:
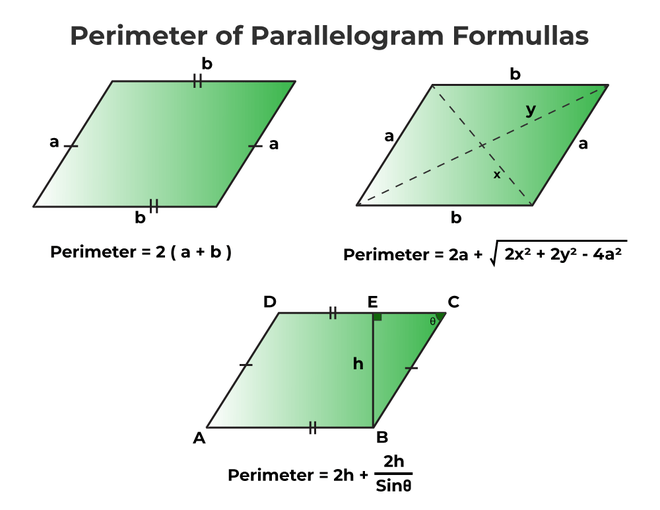
When the adjacent sides of the parallelogram are known:
P = 2(a + b) units,
Where a and b are the sides of the parallelogram.
When one side and the lengths of the diagonals are known:
P = 2a + √(2x2 + 2y2 - 4a2),
Where x and y are the lengths of diagonals and a is the length of the side.
When any angle, base, and height are known:
P = 2a + 2h/sinθ,
Where a is the side of the parallelogram, h is the height of the parallelogram, θ is the angle of the parallelogram.
Now that the formulas of all three cases are known let's derive the formulas of the perimeter of a parallelogram for all three cases,
Perimeter of Parallelogram Formula with Sides
The perimeter of the parallelogram formula with sides is the formula to calculate the perimeter. Below is the derivation for the perimeter of the parallelogram. Let's say the sides of the parallelogram are "a" and "b".
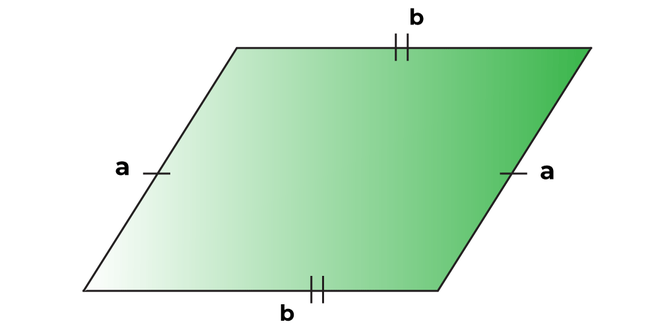
Perimeter = side 1 + side 2 + side 3 + side 4
Side 1 is also known as the base of a parallelogram.
The opposite sides of a parallelogram are equal.
- Side 1 = side 3
- Side 2 = side 4
- Side 3 = a
- Side 4 = b
Perimeter = a + b + a + b
Perimeter = 2 (a + b)
Hence, the perimeter of a parallelogram is twice the sum of its two adjacent sides.
Perimeter of Parallelogram Formula with One Side and Diagonals
The perimeter of the parallelogram formula when one side and the length of both diagonals are given is derived below. Let's say the length of the diagonals are "x" and "y" and the length of the side is "a", from the law of cosines, the cosine formula is applied:

In △ABD:
- x2 = a2 + b2 - 2ab cos∠BAD
In △ADC:
- y2 = a2 + b2 - 2ab cos∠ADC
Adding the equations:
- x2 + y2 = 2 (a2 + b2) - 2ab (cos∠BAD + cos∠ADC)
Now since according to the properties of parallelogram, the adjacent angles of a parallelogram are supplementary, therefore,
∠BAD + ∠ADC = 180
∠BAD = 180 - ∠ADC
Adding cosine on both sides:
cos∠BAD = cos(180 - ∠ADC)
cos∠BAD = -cos∠ADC
Substituting the angle,
x2 + y2 = 2 (a2 + b2) - 2ab (-cos∠ADC + cos∠ADC)
x2 + y2 = 2 (a2 + b2) - 2ab (0)
x2 + y2 = 2 (a2 + b2)
Now finding the value of the b side from the equation formulated above:
b = √[(x2 + y2 - 2a2)/2]
Now that both sides of the parallelogram are known, using the formula for the perimeter of a parallelogram with sides,
P = 2(a + b)
P = 2a + 2(√[(x2 + y2 - 2a2)/2])
P = 2a + √(2x2 + 2y2 - 4a2)
Perimeter of Parallelogram with Base, Height, and Angle
In order to find the perimeter of a parallelogram with base, height, and angle, let's assume the base of the parallelogram is "b", the height of the parallelogram is "h", and the angle of the parallelogram is "θ".
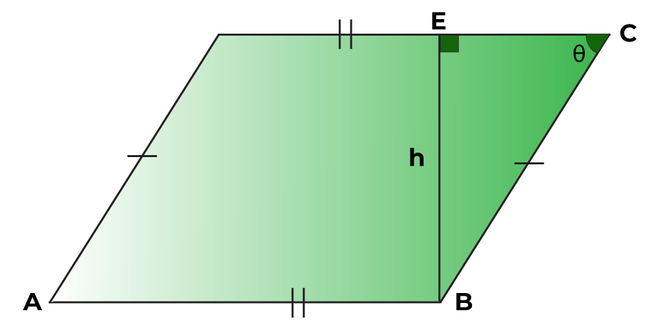
Applying sin function:
Now, the length of the side "b" is known to us in terms of angle. Substituting the value of "b" in the formula:
P = 2(a + b)
P = 2a + 2h/sin θ
Note: θ can be the angle of any vertex of the parallelogram and the formula will remain the same.
Relationship Between Area and Perimeter of Parallelogram
We can find the relation between the area and perimeter of a parallelogram because both the formulas contain sides of the parallelogram, the formula for the area of parallelogram and perimeter of a parallelogram is:
Area of parallelogram = A = b × h square units ⇢ (1)
Perimeter of a parallelogram = P = 2a + 2b units ⇢ (2)
Finding the value of b from equation (2)
P/2 = a + b
b = P/2 - a
Substituting the value of "b" obtained in equation (1)
A = (P/2 - a) h square units
Table of Perimeter Formulas for a Parallelogram
Below is the table demonstrating various formulas to find the Perimeter of a Parallelogram.
| Values Given | Formula |
|---|
| When the sides (a and b) are given | P = 2(a + b) |
| When one side and diagonals are given | P = 2a + √(2x2 + 2y2 - 4a2) |
| When base, height, and angle are given | P = 2a + 2h/sin θ |
Related Articles
Solved Examples on Perimeter of Parallelogram
Example 1: Find the perimeter of a parallelogram with side length = 14m, base = 10m.
Solution:
The perimeter of parallelogram is given by:
2(a + b)
Where, a and b are its two adjacent sides
Perimeter = 2 (14 + 10)
Perimeter = 2 (24)
Perimeter = 48m
Example 2: Find the perimeter of a parallelogram whose base is 5cm, and the side length is 6cm.
Solution:
The perimeter of a parallelogram is given by:
2(a + b)
Where, a is the base and b is its adjacent side
Perimeter = 2 (5 + 6)
Perimeter = 2 (11)
Perimeter = 22cm
Example 3: What is the perimeter of a parallelogram with a side length of 8 in, and diagonals are 12in and 10in?
Solution:
The formula for the perimeter when one side and the lengths of diagonals are known,
P = 2a + √(2x2 + 2y2 - 4a2)
P = 2 × 8 + √(2(12)2 + 2(10)2 - 4(8)2)
P = 16 + √(288 + 200 - 4(64))
P = 31.23 in.
Example 4: What is the perimeter of a parallelogram when the height is 20cm, the vertex angle is 45°, and one of the sides is 12cm?
Solution:
The perimeter of a parallelogram is given by:
P = 2a + 2h/sinθ
P = 2 × 12 + 2 × 20/sin45
P = 24 + 40 × 2
P = 24 + 80
P = 104 cm
Example 5: The perimeter of a parallelogram is 100cm, and one of the sides of the parallelogram is 32cm; find the length of the other side.
Solution:
The perimeter of a parallelogram is given by:
P = 2(a + b)
Where a and b are its two adjacent sides
Given: P = 100cm, a = 32cm
100 = 2 (32 + b)
50 = 32 + b
b = 18cm
The length of the other side of the parallelogram is 18cm.
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice