Point Symmetry, Origin Symmetry, or Central Symmetry is a type of symmetry where an object or shape looks the same when rotated 180° (a half-turn) around a central point.
In this article, we will discuss Point Symmetry in detail, including its definition and examples, as well as some real-life examples from nature.
What is Symmetry?
Symmetry means that you can split a shape or thing into two parts that look the same. In a symmetrical thing, one side is like a mirror image of the other. The imaginary line you can fold along to make those matching halves is called the line of symmetry.
What is Point Symmetry?
Point symmetry is when any object or anything looks the same after turning it 180° around a central point, or we can say, from a certain point, when an object is flipped at 180°, it gives an equal or identical shape. It's like a spinning toy that stops looking different no matter how you turn it.
The center is the point where it stays unchanged, creating a balanced, matching shape on both sides. To check whether an image creates point symmetry or not, two conditions should be fulfilled:
- Every part of the shape is at the same distance from the center.
- Each part and its matching part point in opposite directions.
Definition of Point Symmetry
Point symmetry, also known as central symmetry, is a geometric property exhibited by certain shapes or figures.
An object is said to have point symmetry if there exists a central point around which the object can be rotated by a certain angle, typically 180°, and still maintain its original appearance.
In simpler terms, if the shape looks unchanged after a half-turn (180-degree rotation) around a specific point, it possesses point symmetry.
How to Identify Point Symmetry?
To identify point symmetry, we can use the following steps.
- Identify the Center: Point symmetry occurs when there is a central point around which the object is symmetrical. Locate this central point.
- Check for Symmetry: Examine the object to see if it looks the same when rotated 180° around the central point. If the shape aligns with itself after the rotation, it possesses point symmetry.
- Consider Reflection: Another way to identify point symmetry is by checking if the object is identical on both sides when reflected across the central point.
- Verify in Multiple Directions: Ensure symmetry by checking for consistency in various directions from the central point.
Point Symmetry in Geometric Shapes
In various geometric shapes, such as a square, a rectangle, a parallelogram, a circle, a star, etc., we can observe the point symmetry, which is discussed as follows:
Point Symmetry of Square/Rectangle
- Center: The center of point symmetry for a square or rectangle is the intersection point of its diagonals.
- Symmetry Check: When rotated 180° around this central point, the square or rectangle looks the same. Additionally, reflection across the center results in identical shapes on both sides.

Read More about the Square and Rectangle.
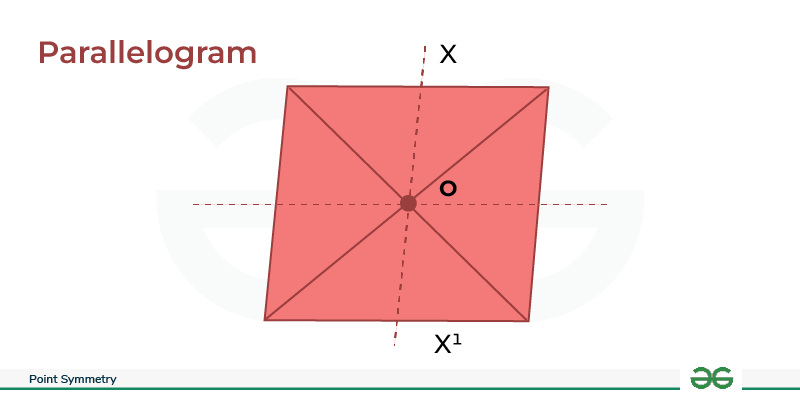
Point Symmetry of Parallelogram
- Center: The point of symmetry in a parallelogram lies at the intersection of its diagonals.
- Symmetry Check: Similar to a square or rectangle, a parallelogram exhibits point symmetry if rotating it 180° or reflecting it across the central point maintains its original appearance.
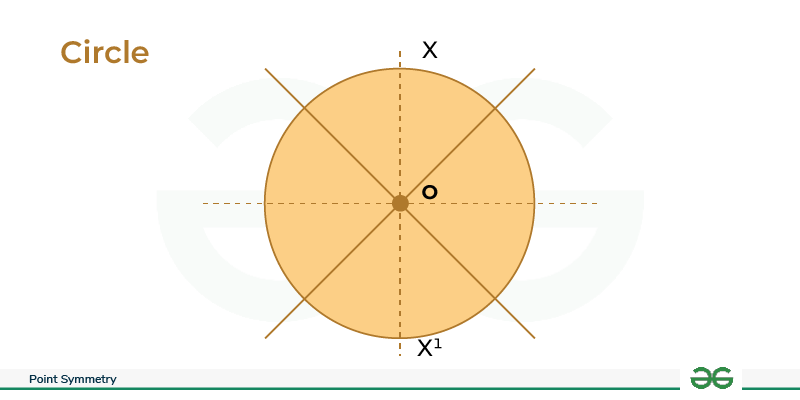
Point Symmetry of a Circle
- Center: The center of the circle serves as the point of symmetry.
- Symmetry Check: A circle is inherently symmetric. Rotating it by any degree around the center results in an identical shape.
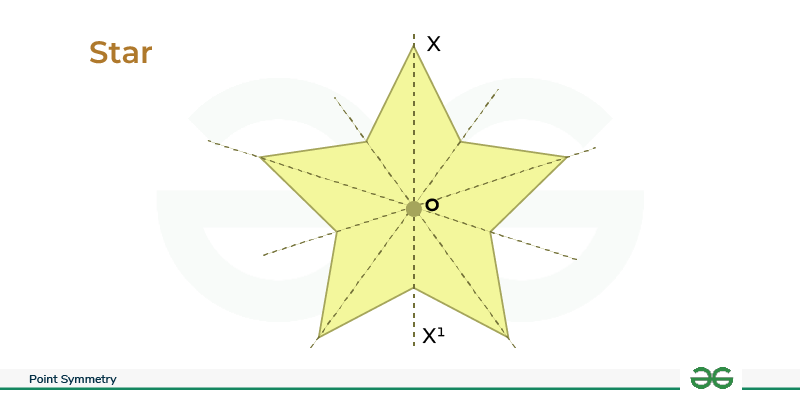
Point Symmetry of a Star
- Center: For a symmetrical star, the center is often the midpoint of its vertical axis.
- Symmetry Check: The star shows point symmetry when rotated by certain angles around its central point. Reflection across this point also reveals symmetry.
Point Symmetry in Letters
When you have point symmetry in the alphabet, it means that if you draw a line through a certain point, the parts on either side of that point are the same distance from it. In English letters, you can find point symmetry.
Take the letter O, for example. It has a center point, and the parts on opposite sides are the same but facing different ways. Uppercase letters like C, D, H, I, N, O, X, and Z also have point symmetry. If you draw a line from the middle of C, D, H, I, O, or X, both the upper and lower parts will be the same length. So, these letters have both point and line symmetry.

Point Vs Reflection Symmetry
The key differences between point symmetry and reflection symmetry are:
Difference Between Point and Reflection Symmetry |
|---|
| Characteristic | Point Symmetry | Reflection Symmetry |
|---|
| Definition | Occurs when a figure is unchanged by rotating it 180° around a central point, known as the center of symmetry. | Occurs when a figure remains unchanged when reflected across a line, known as the line of symmetry. |
|---|
| Type of Transformation | Involves rotation around a central point. | Involves reflection across a line. |
|---|
| Symmetry Element | Center of Symmetry (Point) | Line of Symmetry |
|---|
| Types of Figures | Commonly found in circular or radially symmetric figures. | Commonly found in figures with bilateral symmetry, like rectangles, squares, or letters of the alphabet. |
|---|
| Number of Elements | Only one central point of symmetry. | It can have multiple lines of symmetry depending on the figure. |
|---|
| Example | The letter "O" has point symmetry because it remains the same when rotated 180° around its center. | The letter "H" has reflection symmetry because it remains the same when reflected across a vertical line. |
|---|
| Nature of Symmetry Operation | Rotational | Reflectional |
|---|
Symmetry in Visual Arts
In visual arts, symmetry is a fundamental concept employed to create balance and harmony in compositions. Artists use symmetrical arrangements, where one side mirrors the other, to instill a sense of order and aesthetic appeal.
Symmetry can be found in various art forms, from paintings and sculptures to graphic designs. It serves as a guiding principle for creating visually pleasing and impactful pieces by ensuring a harmonious distribution of elements.
Architectural Designs and Patterns
Architectural designs often incorporate symmetry to achieve a sense of equilibrium and beauty in structures. Symmetrical elements in buildings, such as matching facades or balanced layouts, contribute to a visually cohesive and pleasing architectural aesthetic.
Patterns, whether in tiling, ornamentation, or structural elements, frequently exhibit symmetry to enhance the overall design. This use of symmetry in architecture transcends cultural and historical contexts, representing a timeless approach to creating structures that are not only functional but also visually captivating.
Point Symmetry in Nature
In nature, point symmetry is not as common as other types of symmetry, like bilateral symmetry, but it can still be observed in various forms:
- Starfish
- Flowers
- Crystals
- Snowflakes
Sample Example on Point Symmetry
Example 1: State whether the following statement is true or false: "Every equilateral triangle exhibits point symmetry."
Solution:
False. Point symmetry means that if you rotate a figure by 180 degrees about a central point, the figure looks exactly the same as before. While an equilateral triangle is highly symmetrical—it has three lines of reflection symmetry and rotational symmetry of 120 degrees—rotating it by 180 degrees does not map it onto itself. This means that an equilateral triangle does not exhibit point symmetry, even though it has other types of symmetry.
Example 2: A figure has a point symmetry at the origin. If point B(-2, 5) is part of the figure, find the coordinates of its image point.
Solution:
Point symmetry involves reflecting a point across a central point (in this case, the origin). When a point is symmetrically located with respect to the origin, its coordinates become the negation of the original coordinates.
For point B(-2, 5), the image point (let's call it B') can be found by negating the coordinates:
B' = (-(-2), -(5))
= (2, -5)
Therefore, the image point B' is (2, -5).
Practice Problems on Point Symmetry
Problem 1: Analyze the following set of points: A(1, 4), B(4, 1), C(-1, -4), and D(-4, -1). Determine if these points form a figure with point symmetry, and if so, identify the point of symmetry.
Problem 2: Identify whether the letter "X" exhibits point symmetry. If yes, describe the point of symmetry; if not, explain why.
Problem 3: Draw a simple figure with point symmetry and describe the coordinates of the point of symmetry.
Problem 4: Given a geometric pattern, analyze whether it displays point symmetry. Provide details on any symmetrical elements.
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice