Principle of Inclusion and Exclusion

Last Updated : 13 Aug, 2025

The Principle of Inclusion and Exclusion (PIE) is a counting technique used to find the size of the union of multiple sets by systematically including and excluding overlapping parts.

It corrects the overcounting that happens when you simply add the sizes of the sets. When sets have overlapping elements, counting them directly can lead to overcounting. The Principle of Inclusion and Exclusion fixes this by alternately adding and subtracting the sizes of the intersection to get the exact total.

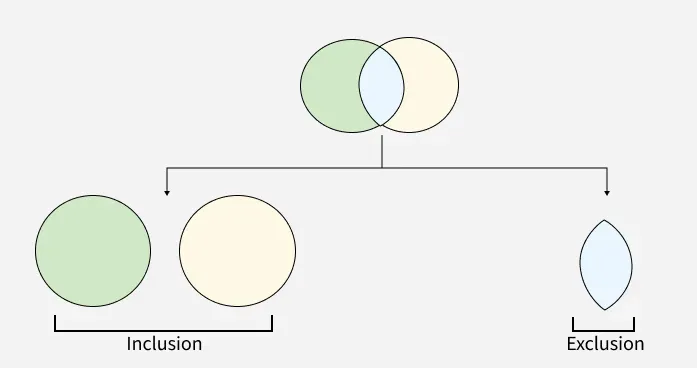
For example, when calculating the number of people who own a dog or a cat, PIE adds up all dog owners and subtracts all cat owners. This includes:

Adding the sizes of each individual set.
Subtracting the sizes of the pairwise intersections to avoid double-counting.
Adding back the size of the intersection of all three sets, as it was subtracted too many times.
Subtracting the sizes of the intersection of four sets, as it was added twice in the last step.
And so on.

Formula for Principle of Inclusion & Exclusion

In general, for n sets A₁, A₂, . . ., A_n:

|A_1 \cup A_2 \cup \dots \cup A_n| = \sum_{i=1}^{n} |A_i| - \sum_{1 \leq i < j \leq n} |A_i \cap A_j| + \sum_{1 \leq i < j < k \leq n} |A_i \cap A_j \cap A_k| - \dots + (-1)^{n+1} |A_1 \cap A_2 \cap \dots \cap A_n|

Where:

The first term sums the sizes of all individual sets.
The second term subtracts the sizes of all pairwise intersections.
The third term adds back the sizes of all three-way intersections.
This alternating pattern continues, with the signs changing for each subsequent term, until the intersection of all N sets is reached.

Note: This formula effectively accounts for all overlaps among the sets, ensuring that each unique element is counted exactly once.

Formula for Two Sets

For two sets A and B

∣AUB∣ = ∣A∣+∣B∣-∣A∩B∣

Where,

∣A∣ is the number of elements in set 𝐴.
∣B∣ is the number of elements in set B.
∣A∩B∣ is the number of elements in both set A and set B.

Formula for Three Sets

For three sets A,B, and C, the Principle of Inclusion and Exclusion (PIE) formula to find the size of the union is:

∣AUBUC∣ = ∣A∣+∣B∣+∣C∣-∣A∩B∣-∣A∩C∣-∣B∩C∣+∣A∩B∩C∣

Where,

∣A∣, ∣B∣, and ∣C∣ are the number of elements in the sets A, B, and C, respectively.
∣A∩B∣, ∣A∩C∣, ∣and B∩C∣ are the numbers of elements in the pairwise intersections of the sets.
∣A∩B∩C∣ is the number of elements that are in all three sets.

Derivation of the Inclusion and Exclusion Principle Using Venn Diagrams

We can visualize this using a Venn diagram for a finite number of sets. Here we will discuss the formula for the Principle of Inclusion and Exclusion for two and three sets and derive it using a Venn diagram.

Venn Diagram for Two Sets

First Step (Inclusion): Add the sizes of the two sets ∣A∣ and ∣B∣. This counts all the elements in A and B, but elements in the intersection of A∩and B are counted twice (once in A and once in B).
Second Step (Exclusion): Subtract the size of the intersection ∣A∩B∣|A \cap B|∣A∩B∣, because these elements were counted twice in the first step.

Thus, the number of elements in the union of these two sets, ∣A ∪ and B∣, is given by:

∣A∪B∣ = ∣A∣ + ∣B∣ − ∣A∩B∣

Venn Diagram for Three Sets

First Step (Inclusion): Add the sizes of the individual sets ∣A∣, ∣B∣, and ∣C∣. This counts all the elements in A, B, and C, but it also counts the elements in the intersections more than once.
Second Step (Exclusion): Subtract the pairwise intersections ∣A∩B∣, ∣B∩C∣, and ∣C∩A∣ because these elements were counted twice in the first step.
Third Step (Re) Inclusion ): Add back the intersection of all three sets ∣A∩, B∩C∣, as it was subtracted three times (once for each pairwise intersection) in the previous step.

Thus, the number of elements in the union of these three sets, ∣A∪B∪C∣, is given by:

∣A∪B∪C∣ = ∣A∣ + ∣B∣ + ∣C∣ − ∣A∩B∣ − ∣B∩C∣ − ∣C∩A∣ + ∣A∩B∩C∣

Applications in Computer Science

Principle of Inclusion and Exclusion (PIE) is used quite a lot in Computer Science, especially in areas that deal with counting, probability, and combinatorics.

Here are some key applications:

Counting problems in algorithms: When counting arrangements, subsets, or configurations with overlapping constraints.
Cryptography & error-correcting codes: Counting possible keys or codewords that satisfy multiple constraints.
Inclusion–Exclusion in bitmask DP: In dynamic programming on subsets, PIE is often combined with bitmasking to speed up solutions to problems involving all subsets.
Graph theory & network problems: Counting the number of vertices/edges meeting certain properties.

Solved Examples

Question 1: In a class of 100 students:

60 study Math.
45 study Science.
20 students study both Math and Science.

How many students study either Math or Science?

Solution:

As we know, n(A⋃B) = n(A) + n(B) – n(A⋂B)
Given:
n(A) = 60
n(B) = 45
n(A∩B) = 20
n(A⋃B) = n(A) + n(B) – n(A⋂B) = 60 + 45 - 20 = 85
Thus, 85 students study either Math or Science.

Question 2: The probability of getting at least one head is Problem: In a survey of 120 people:

80 people like tea.
70 people like coffee.
50 people like both tea and coffee.

How many people like either tea or coffee?

Solution:

As we know, n(A⋃B) = n(A) + n(B) – n(A⋂B)
Given:
IAI = 80
IBI = 70
IA∩BI = 50
Thus, n(A⋃B) = 80 + 70 - 50 = 100
Thus, 100 people like either tea or coffee.

Question 3: A company has 30 employees, 10 are assigned to Task A, 15 to Task B, and 5 are assigned to both. How many employees are assigned to at least one task?

Solution:

As we know, n(A⋃B) = n(A) + n(B) – n(A⋂B)
Given:
IAI = 10 Task A
IBI = 15 Task B
IA∩BI = 5 Both tasks
Substitute the Values, We get
n(A⋃B) = 10 + 15 - 5 = 20
Thus, 20 employees are assigned to at least one task.

Question 4: In a survey of 200 people:

120 likes pizza.
100 like burgers.
80 like tacos.
60 likes both pizza and burgers.
40 likes both burgers and tacos.
30 likes both pizza and tacos.
20 likes all three: pizza, burgers, and tacos.

How many people like at least one of these three foods?

Solution:

As we know, ∣AUBUC∣ = ∣A∣ + ∣B∣ + ∣C∣ - ∣A∩B∣ - ∣A∩C∣ - ∣B∩C∣ + ∣A∩B∩C∣
Given:
∣A∣ = 120 Pizza lovers
∣B∣ = 100 Burger lovers
∣C∣ = 80 Taco lovers
∣A∩B∣ = 60
∣A∩C∣ = 30
∣B∩C∣ = 40
∣A∩B∩C∣ = 20
Substituting in the formula, we get,
∣AUBUC∣ = 120 + 100 + 80 - 60 - 30 - 40 + 20 = 190
Thus, 190 people like at least one of the three foods.

Question 5: In a university of 300 students:

150 students take Math.
120 students take Physics.
100 students take Chemistry.
80 students take both Math and Physics.
60 students take both Physics and Chemistry.
50 students take both Math and Chemistry.
30 students take all three subjects.

How many students are taking at least one subject?

Solution:

As we know, ∣AUBUC∣ = ∣A∣ + ∣B∣ + ∣C∣ - ∣A∩B∣ - ∣A∩C∣ - ∣B∩C∣ + ∣A∩B∩C∣
Given:
∣A∣ = 150 (Math),
∣B∣ = 120 (Physics),
∣C∣ = 100 (Chemistry),
∣A∩B∣ = 80
∣A∩C∣ = 60
∣B∩C∣ = 50
∣A∩B∩C∣ = 30
Substituting values, we get
∣AUBUC∣ = 150 + 120 + 100 - 80 - 60 - 50 + 30 = 210
Thus, 210 students are taking at least one subject.

Practice Questions on the Principle of Inclusion and Exclusion

Question 1: In a group of 200 people:

120 people like chocolate.
90 people like vanilla.
50 people like both chocolate and vanilla.

How many people like either chocolate or vanilla?

Question 2: In a class of 100 students:

70 students play football.
60 students play basketball.
50 students play cricket.
30 students play both football and basketball.
25 students play both basketball and cricket.
20 students play both football and cricket.
15 students play all three sports.

How many students play at least one of these three sports?

Question 3: Out of 150 attendees at an event:

80 attended Workshop A.
70 attended Workshop B.
40 attended both Workshop A and Workshop B.

How many people attended at least one workshop?

Question 4: A card is drawn from a deck of 52 cards. What is the probability that it is:

A heart,
A face card (King, Queen, Jack),
Or a red card (hearts or diamonds)?

There are 13 hearts, 12 face cards, and 26 red cards.

Note that:

3 face cards are also hearts,
6 face cards are red.

Question 5: In a school of 300 students:

180 students are enrolled in Math.
150 students are enrolled in Science.
120 students are enrolled in English.
90 students are enrolled in both Math and Science.
80 students are enrolled in both Science and English.
70 students are enrolled in both Math and English.
50 students are enrolled in all three subjects.

How many students are enrolled in at least one subject?

Answer Key

160 people like either chocolate or vanilla.
120 students play at least one of these sports.
110 people attended at least one workshop.
The probability is 8/13.
260 students are enrolled in at least one subject.

Set Theory
Set Theory Formulas
Set Theory Symbols
Union of Sets
Intersection of Sets
Cardinality of Sets

maityavighyw

Improve

Article Tags :

Principle of Inclusion and Exclusion