Semicircle

In geometry, a semicircle is defined as a shape obtained by dividing the circle into two equal halves. It is a one-dimensional set of points that make up half of a circle. It is a circular arc spanning 180 degrees, which is equivalent to π radians, or half of a full rotation. A semicircle has only one line of symmetry, as it exhibits only reflection symmetry.

In this article, we will discuss the concept of a semicircle, including its shape, formula, examples, perimeter, and area.

What is a Semicircle?

A semicircle is a geometric figure that represents half of a circle, formed by dividing a circle along its diameter. It consists of a circular arc and its endpoints, connected by the diameter of the original circle.

The angle formed by the arc is 180° on one side of the diameter. Some semicircle formulas are:

Components of Semicircle

If we cut a circle into two halves then the two shapes so formed are called the semicircle. Some real-life examples of the semicircle are the protractor, half moon, half pizza, etc.

Radius of Semicircle

The line segment joining the center of the semicircle to the circumference of the semicircle is called its Radius. In the image added above, OA and OB are radius of semi-circle and OA = OB (r).

Diameter of Semicircle

The line segment joining two points on the circumference of semicircle and passing through the center is called its diameter. A semicircle has one diameter only. In that image added above, AB is the diameter (d) of the circle.

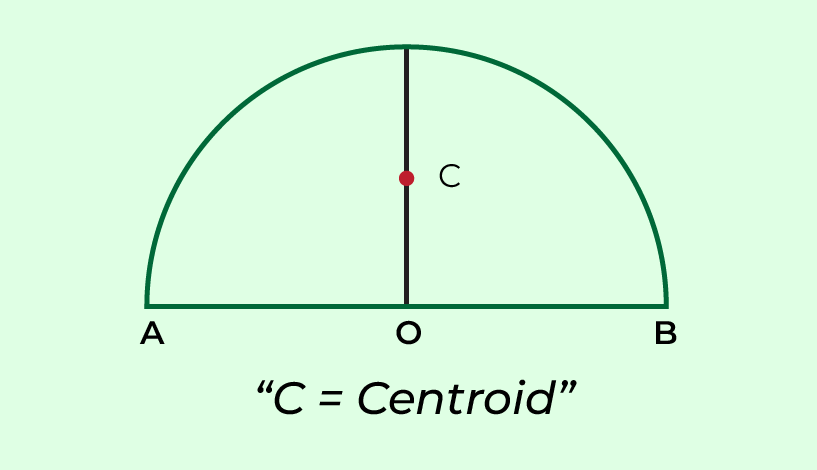
Centroid of Semicircle

Centroid of any closed figure is a point that lies in the middle of the figure, be it centroid of a triangle or any other closed figure. Hence, Centroid of a Semicircle is a point that lies exactly in the middle along the vertical radius of the semicircle.

Let us consider if the center of the semicircle is placed at the origin then x = 0 and from definition we know that centroid of semicircle lies along vertical axis i.e. along the y-axis. In such case the centroid will lie at y = 4r/3π distance from the origin.

Properties of Semicircle

There are several properties of the semicircle. Some of properties of semicircle are,

• Semicircle is a two-dimensional shape.
• Semicircle is half of the circle.
• Semicircle has a curved edge, so it is not a polygon.
• Semicircle is formed by the half of the circumference of the circle and a diameter.
• The area of semi circle is half the area of the circle.
• Angle formed inside a semicircle on its circumference is equal to 90°

Semicircle Area

Area of the semicircle is given by half of the area of circle because the semicircle is half of the circle. The formula for the area of the semicircle is:

Area of Semicircle = (Area of Circle)/2

Area of Semicircle = (πr²)/2

where,

• r is the Radius of Semicircle
• π = 22 / 7 or 3.14

Area of Semi-Circle is measured in Square Units.

Example : Find the area of semicircle with radius 14 cm

Area of Semicircle(A) = (πr²)/2

A = (22/7).(14).(14)/2

A = 308 cm²

Learn More :

• Area
• Area of Circle

Circumference of Semicircle

Circumference of the semicircle is given by half of the circumference of circle because semicircle is half of the circle. The formula for the semicircle's circumference is:

Circumference of Semicircle = (2πr) / 2

Circumference of Semicircle = πr

where,

• r is the Radius of Semicircle
• π = 22 / 7 or 3.14

Semicircle Perimeter

Perimeter of semicircle refers to the sum of the circumference of the semicircle and the diameter of the semicircle. The formula for the perimeter of semicircle is given by:

P_semicircle = Circumference of semicircle + Diameter of semicircle

P_semicircle = πr + d

P_semicircle = πr + 2r, where [d = 2r]

Perimeter of Semicircle = (πr + 2r)

where,

• r is Radius of Semicircle
• π = 22 / 7 or 3.14

Perimeter of Semi-Circle is measured in units such as m, cm, etc.

Example : Find the perimeter of semicircle with radius 14 cm

Perimeter of Semicircle (P) = (π + 2)r

P = (22/7 + 2).14

P = 72 cm

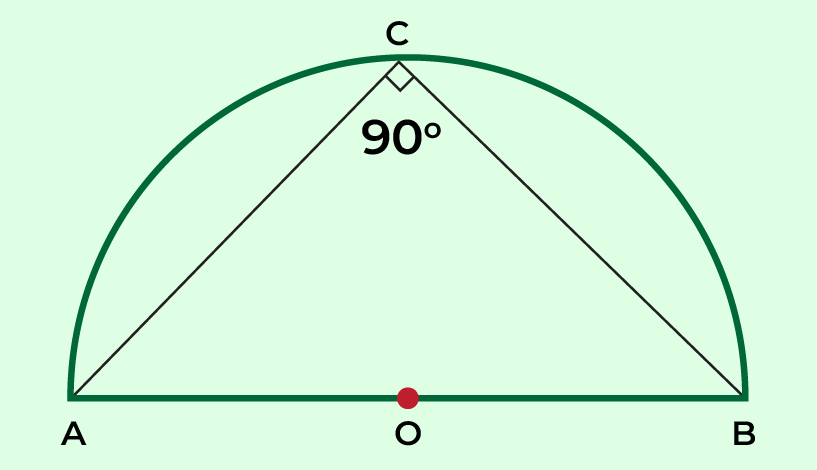
Angles Inscribed in Semicircle

Angle formed by the two lines drawn from the endpoints of the diameter at any point on the semicircle is called as the angle inscribed in a semicircle. Angle inscribed in a semicircle is equal to 90° i.e., right angle. The diameter of semicircle has an angle of 180°as it is a straight line.

People Also Read:

• Geometric Shapes
• Volume Formulas
• Surface Area Formulas

Solved Example Problems on Semicircle

Some examples related to semicircle are,

Example 1: Find the perimeter of semicircle if diameter of semicircle is 4cm.

Solution:

Given,

• d = 4 cm

Perimeter of Semicircle(P) = (πr + d)

r = d / 2 = 4/2 = 2 cm

P = (2π + 4) cm

P = 2(π + 2) cm

P = 10.28 cm

Example 2: Find the area of semicircle with radius 5 cm.

Solution:

Given,

• Radius = 5 cm

Area of Semicircle(A) = [πr²] / 2

A = [π(5)²]/2

A = [25π]/2

A = 39.25 cm²

Example 3: Find the circumference of semicircle if the diameter of semicircle is 8 cm.

Solution:

Diameter(d) = 8 cm

Circumference of Semicircle(C) = πr

Radius of Semicircle(r) = d / 2 = 8 / 2 = 4 cm

C = π(4)

C = 12.56 cm

Example 4: Find the diamter of semicircle whose area is 157cm².

Solution:

Given,

• Area of Semicirlce = 157 cm²

Area of Semicircle = [πr²] / 2

157 = [πr²]/2

314 = [πr²]

r² = 314/π

r² = 314/3.14

r² = 100

Radius of Semicircle(r) = 10 cm

Example 5: Find the radius if the circumference of semicircle is 314 cm.

Solution:

Given,

• Circumference(C) = 314 cm

Circumference of Semicircle = πr

Radius of semicircle(r) = 314/3.14

r = 100 cm

Example 6: The radius of semicircle is given 2 cm find its perimeter.

Solution:

Given,

• Radius of Semicircle(r) = 2 cm

Perimeter of Semicircle(P) = r[π + 2]

P = 2[π + 2]

P = 10.28 cm

Practice Problems on Semicircle

Various practice problems related to semicircle are,

Q1. Find the area of semicircle, given the radius of semicircle is 3cm.

Q2. Find the circumference of semicircle if the radius of the semicircle is 5cm.

Q3. Given the circumference of semicircle 4cm and diameter is 3cm. Find the perimeter of semicircle.

Q4. Find the perimeter of the semicircle, given the radius of semicircle is 6cm.

Conclusion

The semicircle is a fundamental geometric shape that has a wide range of applications and many practical uses, from basic geometry to more advanced mathematical concepts. Knowing how to calculate its area and perimeter helps solve various problems in fields like design and engineering. Its simple properties make it useful in both learning and real-world applications.