Sphere: Definition, Formulas, Examples, Shapes, Properties
Last Updated :
23 Jul, 2025
A sphere is a three-dimensional object that is perfectly round and symmetrical. It is defined as the set of all points in 3D space that are equidistant from a fixed point (the center). The distance from the center to any point on the surface is called the radius. A sphere is a 3D shape with no edges or corners.

Key characteristics of a Sphere
- Radius: The radius of the Sphere is the distance from the center of the sphere to any point on its surface is called the radius.
- Surface: The surface of a sphere is continuous, without any flat or sharp regions.
- Volume: The interior of the sphere contains a three-dimensional space. The volume of the Sphere is calculated by the formula 4/3πr3, where r stands for radius.
- Symmetry: A sphere exhibits rotational symmetry, meaning it looks the same from any angle of rotation around its center.
Volume and surface area formula for Sphere are as follows:
Volume of a Sphere (V) = 4/3πr3
Surface Area of a Sphere (A) = 4πr2
Where,
- π is a Mathematical Constant
- r is Radius of Sphere
Formulas for diameter, area, and volume are given in the following table:
| Sphere | Formula |
|---|
| Surface Area (A) | 4πr2 |
|---|
| Volume (V) | (4/3)πr3 |
|---|
| Circumference of Circle | 2πr |
|---|
| Diameter (d) | d = 2r |
|---|
| Radius (r) | r = d/2 [Given the diameter] |
|---|
People also view: Sphere Formulas
Examples of Sphere
Real-life Applications of the sphere include the following:
- Basketball
- Soccer ball
- Tennis ball
- Marbles
- Moon
- Balloons
- Oranges
 Real Life Applications of Sphere
Real Life Applications of SphereDifference between Sphere and Circle
The following is the list of Difference between Sphere and Circle:
Property | Circle | Sphere |
|---|
Dimension | Two-Dimensional shape | Three-Dimensional Shape |
|---|
Geometry | Closed Curve | Infinite set of points in a plane |
|---|
Equation | (x – h)2 + (y – k)2 = r2 | Infinite set of points in a plane |
|---|
Example | Tire, Coin, Pizza, etc. | Globe, Basketball, etc. |
|---|
Some sphere formulas are added below,
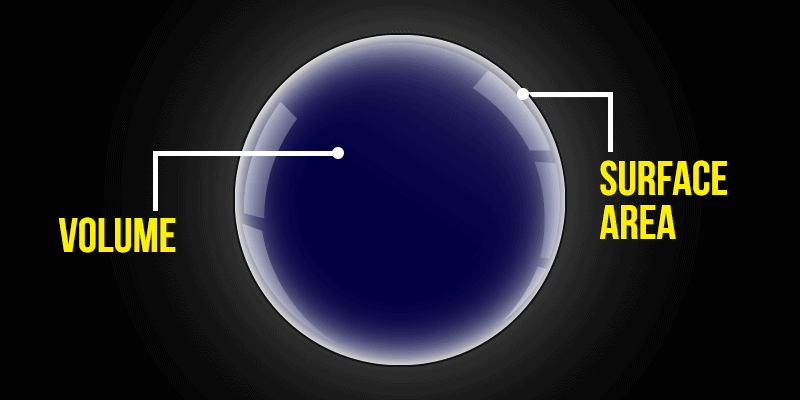
Surface Area of a Sphere
The total surface of a sphere, including the curved surface, is the same in three dimensions. This implies that the area of a sphere's curved surface must be utilized as the foundation rather than the contribution of its circular base to calculate its surface area.
Curved Surface Area of Sphere = Total Surface Area of Sphere
Surface Area of Sphere Formula
"Surface Area" represents the total surface area of the sphere's outer surface.
Surface Area of Sphere = 4πr² square units
Volume of a Sphere
The volume of a sphere indicates the space it occupies. Cubic units, such as cubic meters (m3), cubic centimeters (cm3), and cubic inches (in3), are used to measure this quantity. A sphere, known as a three-dimensional sphere, has uniformly spaced points from its center. Basketballs and soccer balls serve as examples of commonly used spheres, each possessing a unique volume.
Sphere Volume Formula
The volume of a sphere is the amount of space occupied by the sphere's interior. The following formula applies to spheres of various sizes and is a fundamental concept in geometry and mathematics.
Volume of Sphere = 4/3 πr3
Read more on How to Find the Volume of Sphere.
Sphere Equation in 3D
The equation for a sphere in three-dimensional space is given by:
(x - h)2 + (y - k)2 + (z - l)2 = r2
Where,
- (x, y, z) are Coordinates of a Point in 3D space.
- (h, k, l) are Coordinates of Center of sphere.
- r is Radius of Sphere
This equation describes all the points (x, y, z) that are at a distance r from the center (h, k, l) in three-dimensional space. The squared terms on the left side of the equation ensure that the distance calculation is always positive.
Hemisphere Definition
The term "hemisphere" can be broken down into "hemi," meaning half, and "sphere," referring to a three-dimensional shape. Consequently, a hemisphere is a 3D geometric form that represents half of a sphere, with one side being flat and the other resembling a rounded bowl. It comes into existence when a sphere is sliced exactly at its center along its diameter, resulting in two identical hemispheres. The flat side of a hemisphere is often referred to as its base or face.
Surface Area of Hemisphere
Surface Area of Hemisphere = 3πr2
Where,
- π is Mathematical Constant ( π = 3.142)
- "r" is Radius of Hemisphere
Volume of Hemisphere
Volume of Hemisphere = (2πr3)/3
Where,
- π is Mathematical Constant ( π = 3.142)
- "r" is Radius of Hemisphere
Read in Detail:
Surface Area of Hemisphere
Volume of Hemisphere
Difference Between Hemisphere and Sphere
Spheres and hemispheres are both round shapes but there are some certain distinctions between both. Some of the common differences between Spheres and Hemispheres are listed in the following table:
Characteristic | Hemisphere | Sphere |
|---|
Shape | Half of a Sphere | A three-dimensional ball or Globe |
|---|
Surface Area Formula | 2πr² | 4πr² |
|---|
Volume Formula | (2/3)πr³ | (4/3)πr³ |
|---|
Faces | Curved Surface and a Flat Base | Entirely Curved Surface |
|---|
Example | Dome | Basketball |
|---|
Hollow Sphere
A hollow sphere, also known as a spherical shell or simply a shell, is a three-dimensional geometric object that is similar in shape to a regular solid sphere but has an empty or hollow interior. A hollow sphere is characterized by two radii: the outer radius (R) and the inner radius (r), where R is greater than r.
Surface Area of Hollow Sphere:
The surface area of a hollow sphere includes both the outer surface area and the inner surface area.
Surface Area of Hollow Sphere = 4π(R2 + r2)
Where,
- π is Mathematical Constant ( π = 3.142)
- R is Outer Radius of Hollow Sphere
- r is Inner Radius of Hollow Sphere
The volume of the areaHollow Sphere
The volume of a hollow sphere can be calculated by subtracting the volume of the inner sphere from the volume of the outer sphere.
Volume of Hollow Sphere = (4/3)π(R3 - r3)
Where,
- π is Mathematical Constant ( π = 3.142)
- R is Outer Radius of Hollow Sphere
- r is Inner Radius of Hollow Sphere
Calculation of Spheres with Diameter
Calculating spheres with diameter means using the diameter measurement to find the sphere's properties. It starts by halving the diameter to find the radius, which is often needed for calculations. With the radius, you can find the sphere's volume, surface area, or other characteristics as required.
Volume of Sphere using Diameter
Volume of a sphere can be determined by its radius or diameter. When the radius is known, the formula is V = (4/3)πr³. However, if the diameter is given instead, we can use the formula V = (πd³)/6 to calculate the volume.
Surface Area of a Sphere using Diameter
The surface area of the Sphere, when its diameter(d) is given, is calculated by the formula,
Surface Area of Sphere = π(D)2
Related Resources,
Solved Examples on Sphere
Some examples of Sphere with their solutions are,
Example 1: Find the curved surface area of a sphere with a radius of 8 cm, using π as 22/7.
Solution:
Given,
Radius = 8cm
Total Surface Area= 4πr2
Curved Surface Area = 4 × 22/7 × 8 × 8
CSA = 804.57cm2
Example 2: Determine the total cost needed to paint a spherical ball with a radius of 9 cm. The cost of painting the ball is INR 7.5 per square cm, and you can use π as 22/7.
Solution:
Given,
Radius = 9cm
Total Surface Area= 4πr2
Curved Surface Area = 4 × 22/7 × 9 × 9
Curved surface area = 1018.28cm2
Cost of painting the ball = 1018.28 × 7.5 = 7637.1
Cost of painting the ball is Rs. 7637.1
Example 3: What is the value of a sphere if its diameter is 42 cm?
Solution:
Given,
Diameter = 42 cm
Radius = 21 cm
Volume of Sphere(V) = 4/3.π.(r)3
V = 4/3.22/7.(21)3 = 38792 cm3
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice