A superset is a set that contains all the elements of another set. For example, if set A = {21, 22, 23, 24} and set B = {21, 23, 24}, we say that set A is the superset of set B. Because all the elements of B [(i.e.,)21, 23, 24] are in set A.
The following illustration shows the relationship between the set and its superset using a Venn Diagram.
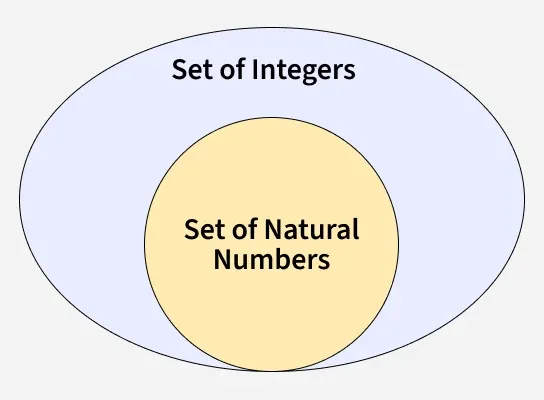
Set A is termed the superset of set B (denoted as A ⊇ B) if all elements of set B are also elements of set A. In other words, every element in B must be contained in A.
Superset Symbol
The superset symbol, often known as the superset operator, is a mathematical symbol that represents the notion of one set being a superset of another.
Here's what the symbols ⊃ and ⊇ stand for:
1) ⊃ (Superset Symbol): This symbol represents a strictly superset connection. If A ⊃ B, then set A is a superset of set B and must contain at least one element not found in set B. In other words, A is larger than B and contains items not present in B.
2) ⊇ (Superset or Equal Symbol): This symbol represents a superset connection that may or may not be equal. If A ⊇ B, it signifies that set A is a superset of set B, and it may include all of the same items as set B, as well as more elements.
Example: Let Y = {21, 22, 23, 24, 25, 26} and X = {21, 22, 23, 25, 26}
In the two sets above, every element of X is also an element of Y, and the number of elements of X is smaller than the number of elements of Y.
In other words, n(x) = 4 and n(Y) = 6
⇒ n(x) < n(Y)
As a result, Y is the superset of X.
Other than this example, we can give all the general sets as supersets of each other as follows:
N ⊃ W ⊃ Z ⊃ Q ⊃ R ⊃ C
Where,
- N is the set of Natural Numbers,
- W is the set of Whole Numbers,
- Z is the set of Integers,
- Q is the set of Rational Numbers,
- R is the set of Real Numbers, and
- C is the set of Complex Numbers.
Proper and Improper Superset
A correct superset is often referred to as a stringent superset. If set X is the correct superset of set W, then all of set W's elements are in X, but set X must have at least one member that is not in set W.
Take, for example, four sets.
- W = {u, v, w}
- X = {u, v, w, x}
- Y = {u, v, w}
- Z = {u, v, y}
Because X is not equal to W, it is the proper superset of W from the sets described above.
- Y is a superset of W, however, it is not a proper superset of W because of Y= W.
- Z is not a superset of W since it lacks the element "w" that is present in set W.
Superset vs Subset
| Superset | Subset |
|---|
| A set that contains all the elements of another set and possibly more. | A set that contains only a portion of another set. |
| A superset includes one or more other sets. | A subset is included within another set (its superset). |
| Usually has a larger number of elements. | Usually has a smaller number of elements. |
| Symbolized as "⊇" or "⊃" in set theory. | Symbolized as "⊆" or "⊂" in set theory. |
| If A = {1, 2, 3, 4, 5} and B = {1, 2, 3, 4, 5, 6}, then B is a superset of A. | If A = {1, 2, 3} and B = {1, 2, 3, 4, 5}, then A is a subset of B. |
Properties of Superset
The following are the main qualities of a superset:
- Every set is a superset of itself.
- Each set is a subset of itself.
- A set has an endless number of supersets.
- Because the null set includes no items, we may claim that any set is a superset of an empty set, for example, every set H would be represented as H ⊃ φ
- Set B is the superset of set A if A is a subset of B.
Related Articles
Solved Examples on Superset
Example 1: Determine who is a subset here if M = {x: x is an odd natural number} and N = {y: y is a natural number}.
Solution:
Given: M = {1, 3, 5, 7, 9, 11,13, …} and N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, …}.
It is obvious that set N contains ALL of the items of set M. As a result, set M is a subset of set N, or M ⊂ N.
Example 2: Show that M is the correct superset of N if M = {32, 33, 37, 39} and N = {32, 37, 39}. Justify your response.
Solution:
Given:
- Set M = {32, 33, 37, 39}
- Set N = {32, 37, 39}
M is the appropriate superset of set N since all of set N's components are also present in set M, however, we can see that set M contains one more additional element (i.e., 33) than set N.
We can also show that set M is not equivalent to set N.
As a result, we may argue that set M is the correct superset of set N.
Example 3: Check whether the following statements are true or false.
a) An empty set is a superset of every other set.
b) Every set is a superset of the empty set.
c) Every set is a superset of itself.
d) Every set has a limited number of supersets.
Solution:
a) False, as empty set do not contain any element.
b) True , as empty set is subset of all sets.
c) True, as set itself contains all the elements it have.
d) False, as we can add one element to set to make it superset, and that element can be anything.
Practice Problems on Supersets
Problem 1: Let A = {1, 2, 3, 4, 5} and B = {2, 4}. Determine whether each statement is true or false:
a) A is a superset of B.
b) B is a subset of A.
c) B is a proper subset of A.
d) A and B are disjoint sets.
Problem 2: Given the sets C = {red, green, blue} and D = {red, green, blue, yellow}. Is D a superset of C or C a superset of D?
Problem 3: Consider the sets E = {a, b, c, d}, F = {c, d, e}, and G = {a, e}. Draw a Venn diagram to represent these sets and their relationships. Identify any supersets or subsets.
Problem 4: Let H = {x, y}. Find the power set of H and identify which subset of H is a superset of the set {x}.
Problem 5: Let M be the set of all mammals and C be the set of all carnivores. Determine whether each statement is true or false:
a) M is a superset of C.
b) C is a subset of M.
c) M is a proper superset of C.
d) C is a proper subset of M.
Explore
Maths
4 min read
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice