There are three sides of a triangle Hypotenuse, Adjacent, and Opposite. The ratios between these sides based on the angle between them is called Trigonometric Ratio. The six trigonometric ratios are: sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec).
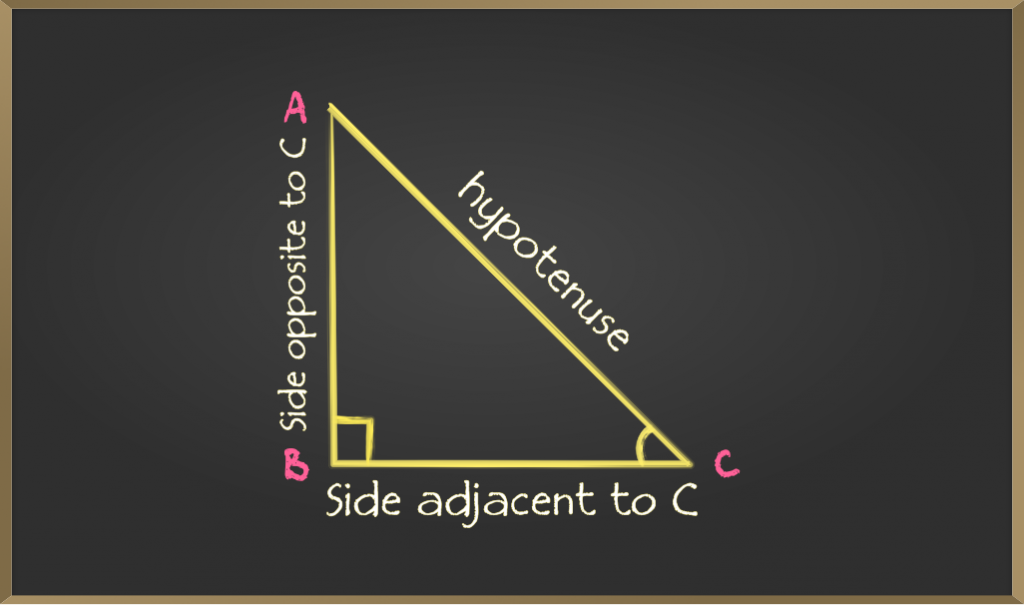
As given in the figure in a right-angle triangle:
- The side opposite the right angle is called the hypotenuse
- The side opposite to an angle is called the opposite side
- For angle C opposite side is AB
- For angle A opposite side is BC
- The side adjacent to an angle is called the adjacent side
- For angle C adjacent side is BC
- For angle A adjacent side is AB
Note: Mathematical symbol θ is used to denote the angle.
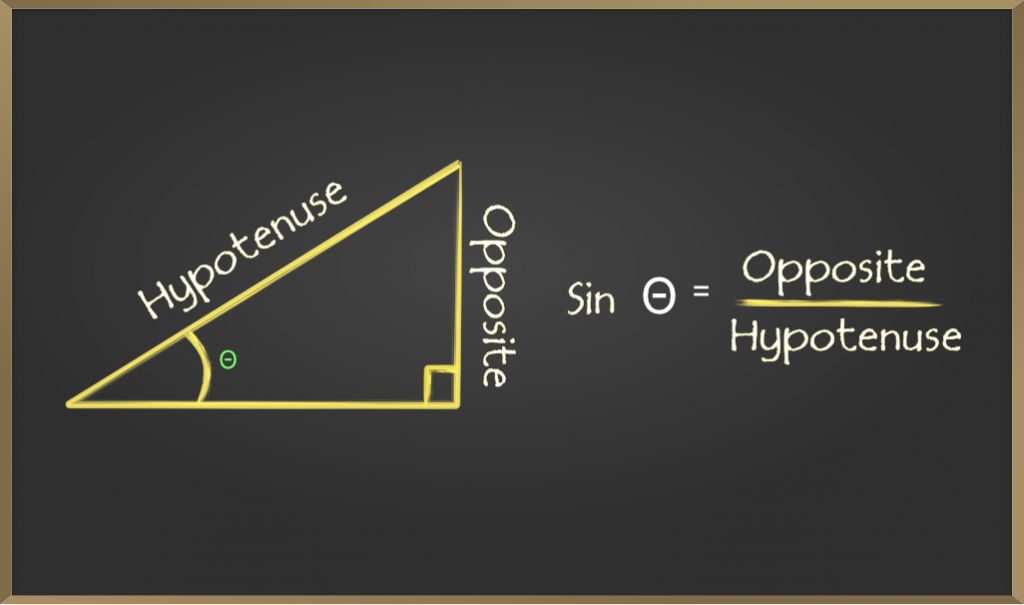
Sine (sin)
Sine of an angle is defined by the ratio of lengths of sides which is opposite to the angle and the hypotenuse. It is represented as sin θ.
Cosine (cos)
Cosine of an angle is defined by the ratio of lengths of sides which is adjacent to the angle and the hypotenuse. It is represented as cos θ

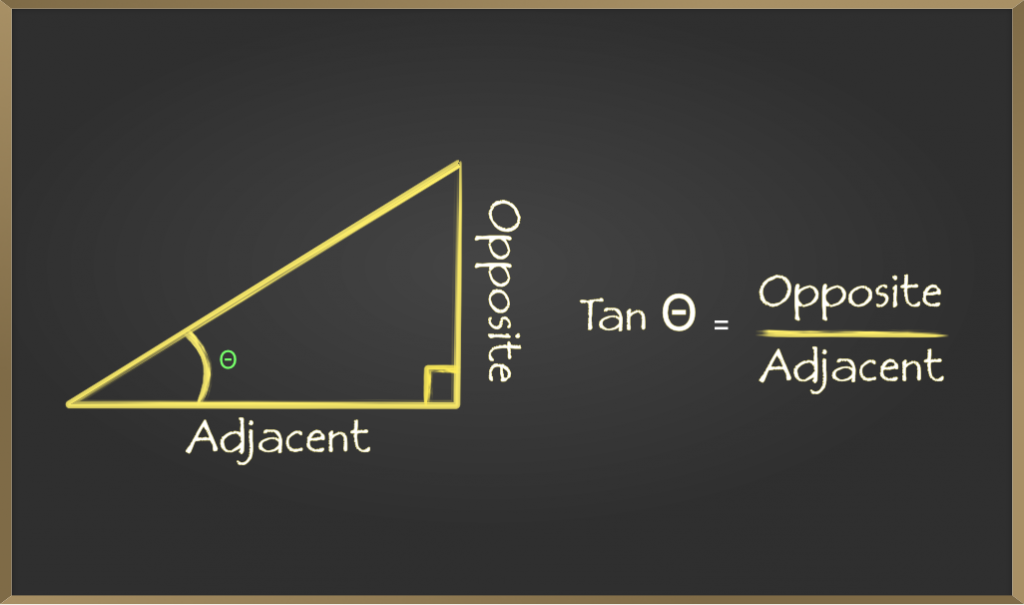
Tangent (tan)
Tangent of an angle is defined by the ratio of the length of sides which is opposite to the angle and the side which is adjacent to the angle. It is represented as tan θ
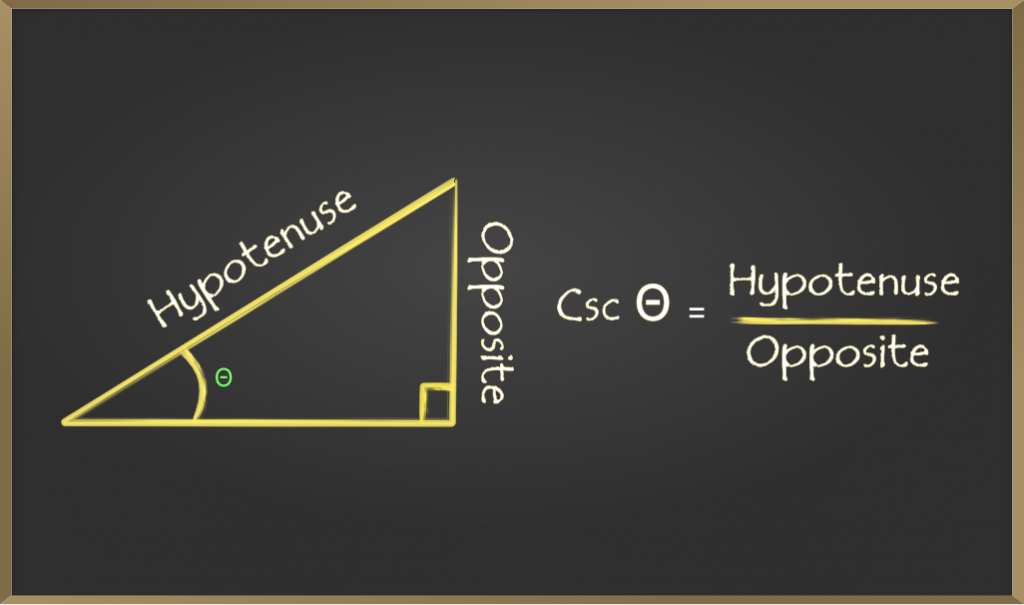
Cosecant (cosec)
Cosecant of an angle is defined by the ratio of the length of the hypotenuse and the side opposite the angle. It is represented as cosec θ
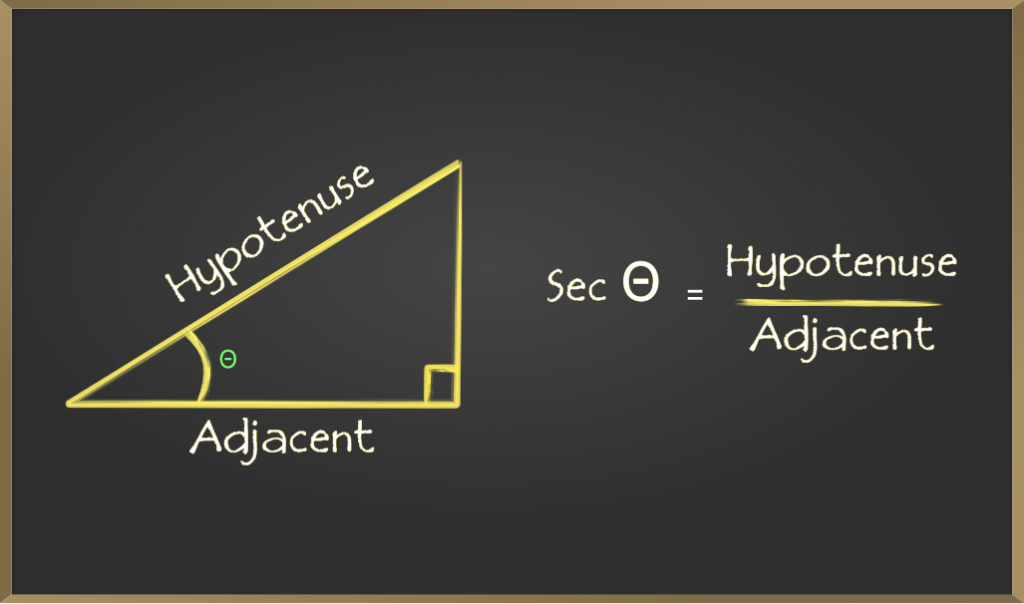
Secant (sec)
Secant of an angle is defined by the ratio of the length of the hypotenuse and the side and the side adjacent to the angle. It is represented as sec θ
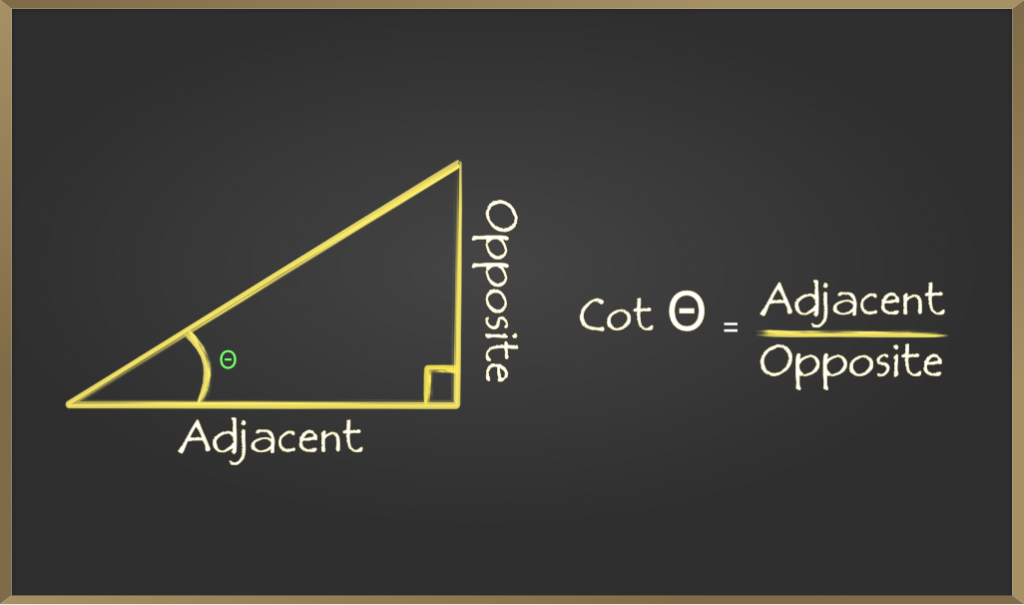
Cotangent (cot)
Cotangent of an angle is defined by the ratio of the length of sides that is adjacent to the angle and the side which is opposite to the angle. It is represented as cot θ.
Values of Trigonometric Ratios for Some Specific Angles
Values of trigonometric ratios for some specific angles, which are commonly used in mathematics, are given in the following trigonometric table:
| Angle (in Degree) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|
| Angle (in Radians) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
|---|
| sin(θ) | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
|---|
| cos(θ) | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
|---|
| tan(θ) | 0 | 1/√3 | 1 | √3 | undefined | 0 | undefined | 0 |
|---|
| csc(θ) | undefined | 2 | √2 | 2/√3 | 1 | undefined | -1 | undefined |
|---|
| sec(θ) | 1 | 2/√3 | √2 | 2 | undefined | -1 | undefined | 1 |
|---|
| cot(θ) | undefined | √3 | 1 | 1/√3 | 0 | undefined | 0 | undefined |
|---|
Next Article: Trigonometry Table
Read: Trigonometry Complete Tutorial
Trigonometric Ratios Examples
Example 1: Find the value of sin θ if tan θ = 4/3 and cos θ = 6/10.
Solution:
Given, tan θ = 4/3 and cos θ = 6/10
We know that, tan θ = sin θ/cos θ
⇒ 4/3 = sin θ/(6/10)
⇒ sin θ = (4/3) × (6/10)
⇒ sin θ = 8/10
Example 2: In a right-angled triangle PQR, right-angled at Q, the hypotenuse is PR = 13 cm, the base is QR = 5 cm and the perpendicular is PQ = 12 cm, and if ∠PQR = θ, then find sin θ, cos θ, and tan θ.
Solution:
Given, in ∆PQR,
- Hypotenuse, PR = 13 cm
- Base, QR = 5 cm
Perpendicular, PQ = 12 cm. Now,
- sin θ = Perpendicular/Hypotenuse = PQ/PR = 12/13
- cos θ = Base/Hypotenuse = QR/PR = 5/13
- tan θ = Perpendicular/Base = PQ/QR = 12/5
Example 3: Find the value of cos θ if tan θ = √3 and sin θ = √3/2.
Solution:
Given, tan θ = √3 and sin θ = √3/2
We know that, tan θ = sin θ/cos θ
⇒ √3 = (√3/2)/cos θ
⇒ cos θ = (√3/2)/√3
⇒ cos θ = 1/2
Example 4: Find the value of sec2 θ if tan2 θ = 1
Solution:
Given, tan2 θ = 1...(1)
we know that, sec2 θ - tan2 θ = 1...(2)
By eq (1),
sec2 θ - 1 = 1
⇒ sec2 θ = 1 + 1
Than, sec2 θ = 2
Related Articles
Explore
Basic Arithmetic
Algebra
Geometry
Trigonometry & Vector Algebra
Calculus
Probability and Statistics
Practice