Types of Polygons

A polygon is a two-dimensional closed geometric figure made up of straight line segments.

Some of the key features are:

• Sides (or edges): The straight line segments that make up the boundary.
• Vertices (or corners): The points where two sides meet.
• Interior: The space enclosed by the sides.

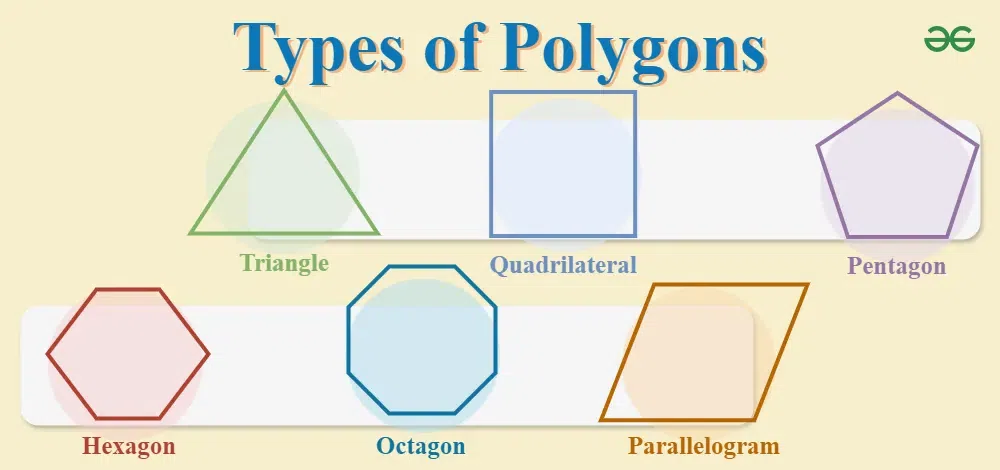
How many Types of Polygons?

Polygons can be classified based on various different parameters, some of these parameters are:

• Based on Boundary of the Polygon
• Based on the Side Length
• Based on Interior Angle
• Based on Sides

Area of a polygon can be easily calculated using polygon formula. Let's discuss types of polygons based on these parameters in detail as follows:

Types of Polygons Based on Boundary of the Polygon

• Simple Polygon
• Complex Polygon

Simple Polygon

A simple Polygon is a closed geometric shape which is constructed using non-intersecting line segments. In simple words, a two-dimensional figure with sides that do not intersect with each other is called a simple polygon. Some of the common examples of simple polygons are triangles, squares, rectangles, pentagons, hexagons, and many more.

Complex Polygon

A complex polygon is a two-dimensional geometric shape that has sides consisting of straight line segments and may have self-intersections or holes. Unlike simple polygons, which do not cross themselves, complex polygons can have edges that intersect each other within the polygon's boundary, resulting in a more intricate and irregular shape.

Complex polygons can be formed by combining simple polygons or by adding cut-outs (holes) within a simple polygon. These cut-outs create regions within the polygon that are not part of the main boundary. The inclusion of self-intersections and holes makes complex polygons more challenging to work with and analyse compared to simple polygons.

Types of Polygons Based on the Side Length

Based on the length of sides, the polygons are classified as follows:

• Regular Polygon
• Irregular Polygon

Regular Polygon

If all the sides and interior angles of the polygon are equal or if a polygon is equiangular and equilateral, then the polygon will be known as a regular polygon. Example square, rhombus, equilateral triangle, etc.

Irregular Polygon

If all the sides and the interior angles of the polygon are of different measure, then the polygon will be known as an irregular polygon. For example scalene triangle, rectangle, kite, etc.

Types of Polygons Based on Interior Angle

Based on the measurement of interior angles the polygons are classified as follows:

• Convex Polygon
• Concave Polygon

Convex Polygon

If all the interior angles of a polygon are strictly less than 180° or equal to it, or if a line segment between two points on the boundary does not go outside the polygon, then the polygon will be known as a convex polygon.

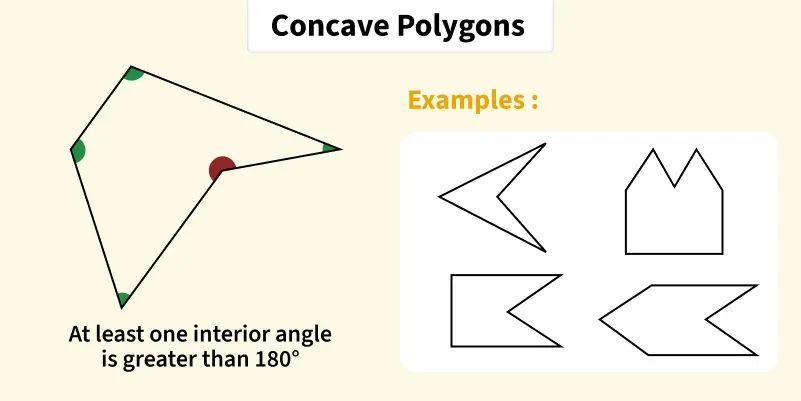
Concave Polygon

If one or more interior angles of a polygon are more than 180° degrees or a polygon contains at least one reflex interior angle, then the polygon will be known as a concave polygon. This polygon can have at least four sides.

Types of Polygons Based on Sides

Polygons are classified based on the number of sides or vertices they have.  So, some of the polygons are:

• Triangles
• Quadrilateral
• Pentagon
• Hexagon
• So on . . .

All of these polygons are given in the following table:

Polygon	Shape	No. of sides	No. of Diagonal	No. of vertices	Interior Angle	Exterior Angle
Triangle		3	0	3	60°	120°
Quadrilateral		4	2	4	90°	90°
Pentagon		5	5	5	108°	72°
Hexagon		6	9	6	120°	60°
Heptagon		7	14	7	128.571°	51.429°
Octagon		8	20	8	135°	45°
Nonagon		9	27	9	140°	40°
Decagon		10	35	10	144°	36°
Hendecagon		11	44	11	147.273°	32.727°
Dodecagon		12	54	12	150°	30°
Triskaidecagon		13	65	13	158.308°	27.692°
Tetrakaidecagon		14	77	14	154.286°	25.714°
Pentadecagon		15	90	15	156°	24°

Triangles(3-gon)

A triangle is a polygon, it is formed with the help of three-line segments intersecting each other, so a triangle has 3 vertices, 3 edges, and 3 angles. The triangles are classified into different types, based on the sides and angles.  

Some properties of the triangle:

• Area of Triangle: 1/2× base × height
• In a triangle, the sum of all the interior angles of a triangle is 180^o.
• The side opposite to the largest angle is the largest side of the triangle.
• The perimeter of a triangle is equal to the sum of the lengths of all three sides of the triangle.

Types: Based on Sides

• Equilateral triangle: If a triangle has all sides equal and angles of equal measure then such types of triangles are known as equilateral triangles.
• Isosceles triangle: If any triangle having any 2 sides equal and angles opposite to the equal sides are equal, then such types of triangles are known as isosceles triangles.
• Scalene triangle: If a triangle has all the 3 sides unequal, then such type of triangles are known as a scalene triangle.

Types: Based on the Angle

• Acute Angled Triangle: A triangle with an angle less than 90° is known as an acute-angle triangle.
• Right Angled Triangle: If any one of the three angles of a triangle is equal to 90° then such type of triangle is known as a right-angle triangle.
• Obtuse Angled Triangle: If any one angle of a triangle is greater than 90°, then such type of triangle is known as an obtuse-angle triangle.

Quadrilaterals (4-gon) 

A Quadrilateral is nothing but a polygon having at least 4 sides. A polygon is formed by enclosing four line segments such that they meet at each other at vertices to make 4 or more angles. Examples of Quadrilateral are Square, Rectangle, Parallelogram, Rhombus, Trapezium.

Some properties of a quadrilateral:

• It has four sides.
• It has four vertices.
• In a quadrilateral, the sum of all the interior angles is 360^o.

Apart from triangle and quadrilateral there are also other polygons but they don't have much use in real life.

Read More,

• Polyhedrons
• Diagonal of Polygon

Sample Problems on Types of Polygon

Question 1: Find the exterior angle of a regular hexagon.

Solution: 

As we know that, hexagon has 6 sides therefore

Exterior Angle = 360^o / n = 360^o / 6

Exterior Angle = 60^o

Question 2: Find the interior angle of a regular pentagon.

Solution: 

As we know that pentagon has 5 sides, therefore

Exterior Angle = 360^o / 5 = 72^o

Interior Angle = 180^o - 72^o = 108^o 

Question 3: Find each interior angle of a regular decagon.

Solution: 

As we know that, decagon has ten sides.

Using angle sum formula, 

As we know that,

S = (n − 2) × 180°

Here, n = 10

Therefore,

Sum of angles of decagon = (10 − 2) × 180°

= 8 × 180° = 1440°

As we know that all the interior angles are equal of a regular decagon, 

Therefore, the measure of each interior angle of regular decagon = sum of interior angles / number of sides

Interior angle = 1440 / 10 = 144°

Hence, Sum of Interior Angle of decagon is 1440° and each interior angle is of 144°.  

Question 4: Find the value of x in the given figure:

Solution:

As we know that the sum of angles os a quadrilateral = 360^o

so, 55^o + 124^o + 70^o + x = 360^o

249^o + x = 360^o

x = 111^o

Question 5: Find the value of x in the given figure:

Solution:

As we know that the sum of exterior angles = 360^o

So, 120^o + 125 + x = 360^o

245^o + x = 360^o

x = 360^o - 245^o

x = 115^o