Pascal's Triangle is a triangular arrangement of numbers where each number is the sum of the two numbers directly above it in the previous row. It is named after the French mathematician Blaise Pascal, although it was studied by mathematicians in various cultures long before him.
Structure of Pascal's Triangle
- The triangle starts with a 1 at the top.
- Each row begins and ends with 1.
- Any other number in the triangle is the sum of the two numbers immediately above it in the previous row.
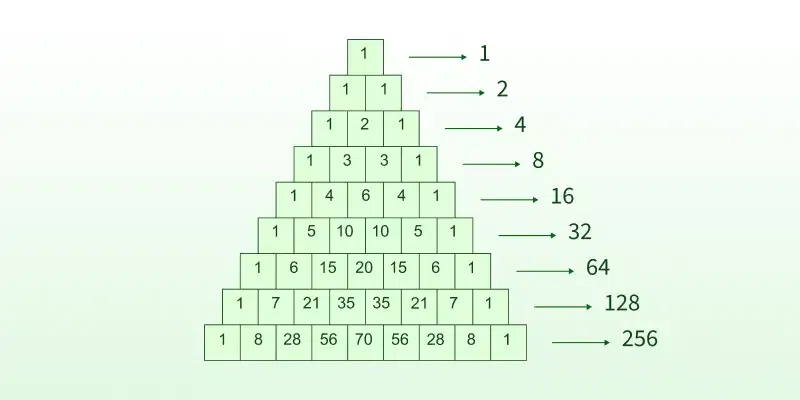 Pascal's Triangle
Pascal's TriangleHistory of Pascal's Triangle
Pascal's Tringale is named after the French mathematician Blaise Pascal, though it was known to mathematicians in ancient India, China, and Persia long before Pascal's time. The earliest known version appeared in China around 1000 BCE, in the works of the mathematician Jia Xian. Later, the Persian mathematician Al-Karaji contributed to its development in the 10th century. The triangle became widely recognized in the West due to Pascal's work in the 17th century, though he did not invent it.
Pascal’s Triangle Patterns
We observe various patterns in Pascal’s triangle they are:
- Diagonals in Pascal’s Triangle
- Binomial Coefficients
- Horizontal Sum
- Prime Numbers in Triangle
- Fibonacci Pattern, etc.
Diagonals in Pascal’s Triangle
Each rightward diagonal of Pascal’s Triangle, when considered as a sequence represents the different numbers such as the first rightward diagonal represents a sequence of number 1, the second rightward diagonal represents triangular numbers, the third rightward diagonal represents the tetrahedral numbers, the fourth rightward diagonal represents the Penelope numbers and so on.
Pascal’s Triangle Binomial Expansion
We can easily find the coefficient of the binomial expansion using Pascal's Triangle. The elements in the (n+1)th row of the Pascal triangle represent the coefficient of the expanded expression of the polynomial (x + y)n.
We know that the expansion of (x + y)n is,
(x + y)n = a0xn + a1xn-1y + a2xn-2y2 + … + an-1xyn-1 + anyn
Here, a0, a1, a2, a3, ...., an are the term in the (n+1)th row of Pascal's Triangle
Horizontal Sum of Rows
On close observing Pascal’s Triangle we can conclude that the sum of any row in Pascal’s triangle is equal to a power of 2. The formula for the same is, For any (n + 1)th row in Pascal’s Triangle the sum of all the elements is, 2n
Applying this Formula in the first 4 rows of Pascal’s triangle we get,
1 = 1 = 20
1 + 1 = 2 = 21
1 + 2 + 1 = 4 = 22
1 + 3 + 3 + 1 = 8 = 23
Exponents of 11
Each row of Pascal's Triangle corresponds to a power of 11:
Row n (starting from n = 0) represents 11n.
Examples:
- Row 0: 1 → 110 = 1
- Row 1: 1, 1 → 111 = 11
- Row 2: 1, 2, 1 → 112 = 121
- Row 3: 1, 3, 3, 1 → 113 = 1331
Note: For higher powers of 11, the digits in the triangle rows exceed single digits, causing a carry-over effect. In such cases, the numbers in Pascal's Triangle no longer directly represent 11n. Instead, the pattern can still be reconstructed by summing the digits appropriately.
Prime Numbers in Pascal’s Triangle
Another very interesting pattern in the Pascals triangle is that if a row starts with a prime number (neglecting 1 at the start of each row), then all the elements in that row are divisible by that prime number. This pattern does not hold true for the composite numbers.
For example, the eighth row in the Pascal triangle is,
1 7 21 35 35 21 7 1
Here, all the elements are divisible by 7.
Fibonacci Sequence in Pascal’s Triangle
We can easily obtain the Fibonacci sequence by simply adding the numbers in the diagonals of Pascal's triangle. This pattern is shown in the image added below,
 Fibonacci & Pascal's triangle relation
Fibonacci & Pascal's triangle relationRead More: Interesting Facts about Pascal's Triangle
Pascal Triangle Formula is the formula that is used to find the number to be filled in the mth column and the nth row. As we know the terms in Pascal's triangle are the summation of the terms in the above row. So we require the elements in the (n-1)th row, and (m-1)th and nth columns to get the required number in the mth column and the nth row.
The elements of the nth row of Pascal's triangle are given, nC0, nC1, nC2, ..., nCn.
The formula for finding any number in Pascal's triangle is:
nCm = n-1Cm-1 + n-1Cm
Where,
- nCm represents the (m+1)th element in the nth row., and
- n is a non-negative integer [0 ≤ m ≤ n]
How to Use Pascal’s Triangle?
We use the Pascal triangle to find the various cases of the possible outcomes in probability conditions. This can be understood by the following example, tossing a coin one time we get two outcomes i.e. H and T this is represented by the element in the first row of Pascal's Triangle.
Similarly tossing a coin two times we get three outcomes i.e. {H, H}, {H, T}, {T, H}, and {T, T} this condition is represented by the element in the second row of Pascal's Triangle.
Thus, we can easily tell the possible number of outcomes in tossing a coin experiment by simply observing the respective elements in the Pascal Triangle.
The table below tells us about the cases if a coin is tossed one time, two times, three times, and four times, and its accordance with Pascal's Triangle
Number of Tosses
OR
A row of Pascals Triangle | Possible Outcomes | Elements in Pascal Triangle |
|---|
1 | {H},
{T} | 1 1 |
2 | {HH},
{HT}, {TH},
{TT} | 1 2 1 |
3 | {HHH},
{HHT}, {HTH}, {THH},
{HTT}, {THT}, {TTH},
{TTT} | 1 3 3 1 |
4 | {HHHH},
{HHHT}, {HHTH}, {HTHH}, {THHH},
{HHTT}, {HTHT}, {HTTH}, {THHT}, {THTH}, {TTHH},
{HTTT}, {THTT}, {TTHT}, {TTTH},
{TTTT} | 1 4 6 4 1 |
Pascal’s Triangle Properties
Various Properties of Pascal's Triangle are,
- Every number in the Pascal triangle is the sum of the number above it.
- The starting and the end numbers in Pascal's triangle are always 1.
- The first diagonal in Pascal's Triangle represents the natural number or counting numbers.
- The sum of elements in each row of Pascal's triangle is given using a power of 2.
- Elements in each row are the digits of the power of 11.
- The Pascal triangle is a symmetric triangle.
- The elements in any row of Pascal's triangle can be used to represent the coefficients of Binomial Expansion.
- Along the diagonal of Pascal's Triangle, we observe the Fibonacci numbers.
Articles related to Pascal's Triangle:
• Binomial Theorem
• Binomial Random Variables and Binomial Distribution
For Programmers: Program to print to Pascal's Triangle
Solved Examples of Pascal’s Triangle
Example 1: Find the fifth row of Pascal’s triangle.
Solution:
The Pascal triangle with 5 row is shown in the image below,

Example 2: Expand using Pascal Triangle (a + b)2.
Solution:
First write the generic expressions without the coefficients.
(a + b)2 = c0a2b0 + c1a1b1 + c2a0b2
Now let’s build a Pascal’s triangle for 3 rows to find out the coefficients.

The values of the last row give us the value of coefficients, c0 = 1, c1 = 2, c2 =1
(a + b)2 = a2b0 + 2a1b1 + a0b2
Thus verified.
Example 3: Expand using Pascal Triangle (a + b)6.
Solution:
First write the generic expressions without the coefficients.
(a + b)6 = c0a6b0 + c1a5b1 + c2a4b2 + c3a3b3 + c4a2b4 + c5a1b5 + c6a0b6
Now let’s build a Pascal’s triangle for 7 rows to find out the coefficients.

The values of the last row give us the value of coefficients.
c0 = 1, c1 = 6, c2 = 15, c3 = 20, c4 =15, c5 = 6 and c6 = 1.
(a + b)6 = 1a6b0 + 6a5b1 + 15a4b2 + 20a3b3 + 15a2b4 + 6a1b5 + 1a0b6
Example 4: Find the second element in the third row of Pascal’s triangle.
Solution:
To find the 2nd element in the 3rd row of Pascal’s triangle.
We know that the nth row of Pascal’s triangle is nC0, nC1, nC2, nC3…
The Pascal Triangle Formula is, nCk = n-1Ck-1 + n-1Ck,where nCk represent (k+1)th element in nth row.
Thus, 2nd element in the 3rd row is,
3C1 = 2C0 + 2C1
= 1 + 2
= 3
Thus, the second element in the third row of Pascal’s triangle is 3.
Similar Reads
CBSE Class 11 Maths Notes
CBSE Class 11 Maths Revision Notes have been designed in the most basic and detailed format possible, covering nearly all domains such as differential calculus, arithmetic, trigonometry, and coordinate geometry. We know how hard it gets when you shift to an altogether new grade where subjects are no
15+ min read
Chapter 1: Sets
Representation of a Set
Sets are defined as collections of well-defined data. In Math, a Set is a tool that helps to classify and collect data belonging to the same category. Even though the elements used in sets are all different from each other, they are all similar as they belong to one group. For instance, a set of dif
7 min read
Types Of Sets
In mathematics, a set is defined as a well-defined collection of distinct elements that share a common property. These elements— like numbers, letters, or even other sets are listed in curly brackets "{ }" and represented by capital letters. For example, a set can include days of the week. The diffe
12 min read
Universal Sets
Universal Set is a set that has all the elements associated with a given set, without any repetition. Suppose we have two sets P = {1, 3, 5} and Q = {2, 4, 6} then the universal set of P and Q is U = {1, 2, 3, 4, 5, 6}. We generally use U to denote universal sets. Universal Set is a type of set that
6 min read
Venn Diagram
Venn Diagrams are used for the visual representation of relationships as they provide a clear, visual method for showing how different sets intersect, overlap, or remain distinct. They are essential tools in mathematics and logic for illustrating the relationships between sets. By employing intersec
14 min read
Operations on Sets
Sets are fundamental in mathematics and are collections of distinct objects, considered as a whole. In this article, we will explore the basic operations you can perform on sets, such as union, intersection, difference, and complement. These operations help us understand how sets interact with each
15+ min read
Union of Sets
Union of two sets means finding a set containing all the values in both sets. It is denoted using the symbol '∪' and is read as the union. Example 1:If A = {1, 3. 5. 7} and B = {1, 2, 3} then A∪B is read as A union B and its value is,A∪B = {1, 2, 3, 5, 7}Example 2:If A = {1, 3. 5.7} and B = {2, 4} t
12 min read
Chapter 2: Relations & Functions
Chapter 3: Trigonometric Functions
Chapter 4: Principle of Mathematical Induction
Chapter 5: Complex Numbers and Quadratic Equations
Complex Numbers
Complex numbers are an essential concept in mathematics, extending the idea of numbers to include solutions for equations that don't have real solutions. Complex numbers have applications in many scientific research areas, signal processing, electromagnetism, fluid dynamics, quantum mechanics, and v
12 min read
Algebra of Real Functions
The algebra of real functions refers to the study and application of algebraic operations on functions that map real numbers to real numbers. A function can be thought of as a rule or set of rules which map an input to an output knows as its image. It is represented as x ⇢ Function ⇢ y. A real funct
5 min read
Algebraic Operations on Complex Numbers
A complex number is a number that includes both a real and an imaginary part. It is written in the form:z = a + biWhere:a is the real part,b is the imaginary part,i is the imaginary unit, satisfying i2 = −1.Algebraic operations on complex numbers follow specific rules based on their real and imagina
7 min read
Polar Representation of Complex Numbers
Complex numbers, which take the form z = x + yi, can also be represented in a way that highlights their geometric properties. This alternative representation is known as the polar form. The polar representation of a complex number expresses it in terms of its magnitude (modulus) and direction (argum
9 min read
Absolute Value of a Complex Number
The absolute value (also called the modulus) of a complex number z = a + bi is its distance from the origin in the complex plane. The absolute value tells you how far a number is from zero, regardless of its direction (positive or negative).It is denoted as ∣z∣ and is given by the formula:|z| = \sqr
7 min read
Conjugate of Complex Numbers
In the world of mathematics, complex numbers are one of the most important discoveries by mathematicians as they help us solve many real-life problems in various fields such as the study of electromagnetic waves, engineering, and physics.The Conjugate of a Complex Number is also a complex number obt
6 min read
Imaginary Numbers
Imaginary numbers are numbers as the name suggests are the number that is not real numbers. All the numbers real and imaginary come under the categories of complex numbers. Imaginary numbers are very useful in solving quadratic equations and other equations whose solutions can not easily be found us
9 min read
Chapter 6: Linear Inequalities
Compound Inequalities
Compound Inequalities are the combination of two or more inequalities. These inequalities are combined using two conditions that are AND, and OR. These conditions have specific meanings and they are solved differently. The inequities in compound inequalities are individually solved using normal rule
10 min read
Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation - Linear Inequalities | Class 11 Maths
A linear inequality is a mathematical expression involving an inequality symbol (<, >, ≤, or ≥) and a linear expression. Unlike linear equations, which give a specific solution, linear inequalities define a range of possible solutions.Example: 2x+3>5 In this case, the inequality indicates t
7 min read
Graphical Solution of Linear Inequalities in Two Variables
We know how to formulate equations of different degree, and it is used a lot in real life, but the question arises, is it always possible to convert a situation into an equation? Sometimes we get statements like, the number of Covid cases per day in Delhi has reached more than 10,000. This phrase “L
8 min read
Solving Linear Inequalities Word Problems
We are well versed with equations in multiple variables. Linear Equations represent a point in a single dimension, a line in a two-dimensional, and a plane in a three-dimensional world. Solutions to linear inequalities represent a region of the Cartesian plane. It becomes essential for us to know ho
10 min read
Chapter 7: Permutations and Combinations
Fundamental Principle of Counting
Fundamental Principle of Counting is the basic principle that helps us to count large numbers in a non-tedious way. Suppose we have to guess the pin of a three-digit code so the number of ways we can guess is 1000 this can be seen as the pin can be, 000, 001, 002, ....., 999 any number between 000,
11 min read
Permutation
In Mathematics, Permutation is defined as a mathematical concept that determines the number of possible arrangements for a specific set of elements. therefore, it plays a big role in computer science, cryptography, and operations research. For example, take a set {1, 2, 3}:All Permutations taking al
15+ min read
Combinations
Combination is a way of choosing items from a set, (unlike permutations) when the order of selection doesn't matter. In smaller cases, it's possible to count the number of combinations. Combination refers to the mixture of n things taken k at a time without repetition.Example: For set S = {a, b, c},
9 min read
Chapter 8: Binomial Theorem
Chapter 9: Sequences and Series
Sequences and Series
A sequence is an ordered list of numbers following a specific rule. Each number in a sequence is called a "term." The order in which terms are arranged is crucial, as each term has a specific position, often denoted as an​, where n indicates the position in the sequence.For example:2, 5, 8, 11, 14,
7 min read
General and Middle Terms - Binomial Theorem - Class 11 Maths
Binomial theorem or expansion describes the algebraic expansion of powers of a binomial. According to this theorem, it is possible to expand the polynomial "(a + b)n" into a sum involving terms of the form "axzyc", the exponents z and c are non-negative integers where z + c = n, and the coefficient
7 min read
Arithmetic Series
An arithmetic series is the sum of the terms of an arithmetic sequence, where an arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. Or we can say that an arithmetic progression can be defined as a sequence of numbers in which for every pair of
5 min read
Arithmetic Sequence
An arithmetic sequence or progression is defined as a sequence of numbers in which the difference between one term and the next term remains constant.For example: the given below sequence has a common difference of 1.1 2 3 4 5 . . . n ⇑ ⇑ ⇑ ⇑ ⇑ . . . 1st 2nd 3rd 4th 5th . . . nth TermsThe Arithmetic
8 min read
Geometric Progression or GP
Geometric Progression (GP) is a sequence of numbers where each term after the first is found by multiplying the previous term by a constant called the common ratio.For Example, the sequence given below forms a GP with a common ratio of 2 1 2 4 8 16 . . . n⇑ ⇑ ⇑ ⇑ ⇑ . . . 1st 2nd 3rd 4th 5th . . . nt
11 min read
Geometric Series
In a Geometric Series, every next term is the multiplication of its Previous term by a certain constant, and depending upon the value of the constant, the Series may increase or decrease.Geometric Sequence is given as: a, ar, ar2, ar3, ar4,..... {Infinite Sequence}a, ar, ar2, ar3, ar4, ....... arn {
3 min read
Arithmetic Progression and Geometric Progression
Arithmetic Progression and Geometric Progression: The word "sequence" in English means a collection of some numbers or objects in such a way that it has a first member, a second member, and so on. Sequences can be of anything, for example. - January, February, .... is the sequence of months in a yea
10 min read
Special Series in Maths - Sequences and Series | Class 11 Maths
Special Series: A series can be defined as the sum of all the numbers of the given sequence. The sequences are finite as well as infinite. In the same way, the series can also be finite or infinite. For example, consider a sequence as 1, 3, 5, 7, … Then the series of these terms will be 1 + 3 + 5 +
10 min read