Sinc Function is an important tool in the electronic industry. They are ubiquitous in modern electronics and are almost used in every daily appliance for analysis of various circuits working. Sinc Function is used in numerous electronic devices and systems, contributing to their design, analysis, and performance optimization.
In this Article, We will be going through the Sinc Function, First, we will start our Article with the Definition of the Sinc Function, Then we will go through the Mathematical Expression of the Sinc Function, then we will see how to generate Sinc Function. At last, We will conclude our article with Advantages, Disadvantages, Applications, and Some FAQs.
What is Sinc Function?
Sinc function is often denoted as Sinc(x). This function is a non-periodic waveform with an interpolating graph. It is an even function with a unity area. It is popularly known as a sampling function and is widely used in signal processing and in the theory of Fourier Transforms.
Also known as sine cardinal, this function is commonly abbreviated as sinc and is defined as the ratio of sin(x) to x resulting in an oscillating graph. The value of the function at origin i.e x=0 is calculated using limits but overall the function is very useful for various analysis.
Sinc Function Graph
If we plot the graph representing the magnitude of the Sinc Function with time, the graph of the Sinc Function looks like this.
-(1).png) sinc(x)
sinc(x)
As we observe, we can see that the graph Sinc Function oscillates very quickly . We also see that the is 0 for all integral values of time except at t=0, where it has a maximum value of π. This property is used largely to avoid intersymbol interference in Digital transmission systems.
If we carefully observe the shape of graph we see that the graph is symmetric about origin making it an Even function.
Mathematical Expression of Sinc Function
Since sinc function is a ratio we can define it mathematically as
Sinc(x)= 1 at x=0
otherwise,
Sinc(x)=sin(πx)/(πx)
The value of function at x=0 is calculated by L'Hôpital's rule and is equal to 1. It is also important to note that the integral of function from -∞ to +∞ is π.
∫ sinc(x)dx = π
Fourier Transform
Let us see how we can get a frequency domain function from a time domain function and a time-domain function from a frequency-domain signal.
X(ω) = ∫x(t)e−jωt dt Forward transform
x(t) = 1/2π ∫ X(ω)ejωt dω Inverse transform
If X(ω) is the Fourier transform of a signal x(t) meaning x(t) is the inverse transform of X(ω)
x(t) ←→ X(ω)
x(t)= FT ←→ X(ω)
This means we can easily analyse a signal in frequency and time domain of either form is given to us
Fourier Analysis of Sinc Function
The main thing that makes Sinc Function a milestone in communication is its Fourier Transform. The Fourier transform of sinc function is rectangular pulse and a rectangular shape in the frequency domain is the idealized “brick-wall” filter response. This makes sinc(x) as the impulse response of an ideal low-pass filter.
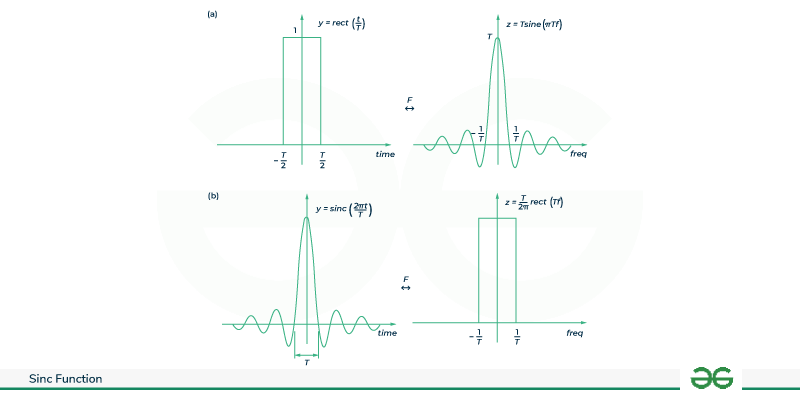 Fourier Analysis of Sinc Function
Fourier Analysis of Sinc Function
How To Generate a Sinc Function ?
Anyone who knows tye representation of sinc Function can easily generate this function. These are the steps:
- Install the required software for representation of the signals. This may include softwares like MATLAB or programming language like python. You can either install it or work on the browser itself.
- Define the input range for which required sinc function should be generated. After this store the corresponding output values using the formula of sinc Function i.e sinc(x)=sin(x)/x.
- In order to see the output use plotting tools to plot the graph which will show the sinc function over the desired input range. The output will look like the graph given below.
 MATLAB output
MATLAB output
Advantages of Sinc Function
The advantages of Sinc Function are stated below:
- Sinc Function form basis of signal analysis. They are crucial for understanding many concepts involved in signal processing thereby making it the base of electronics.
- Its even symmetric nature along with its oscillating property is very useful which is applied in various modulation schemes. As seen in the graph the function shows a maxima at origin and later shows local maxima's and minima's.
- Sinc Function are often used in applications where a Fourier analysis is required. For example they are used in study of Fourier analysis theory.
- It has theoretical application because of its ability to keep original signal intact. This is fulfilled when sampling frequency is at least twice the highest frequency in the signal i.e when Nyquist-Shannon sampling theorem holds true.
- Sinc Function is also used in DACs( Digital to Analog convertors). The reconstruction of original analog signals involves staircase waveforms. To obtain this in frequency domain the idealized spectrum is multiplied by the sinc function to produce the outputs.
Disadvantages of Sinc Function
The disadvantages of Sinc Function are stated below:
- The major disadvantage of sinc Function is that it that it oscillates between negative and positive infinity without dropping amplitude to 0. This can be a major problem when using it in computer applications due to infinite support.
- Due to limited features, these signals have limited applications in communication system. Other signals like sine wave are used more often due to the simplicity and features it offer.
- It has a very slow decay rate which can cause prolonged influence over time. Therefore it is not a practical choice for filters as it stops their ability to differentiate between relevant information.
- Another problem of sinc Function is the presence of side lobes. These lobes can interfere with the message signal in-case the sampling time instants are small resulting in complicated filtering tasks with noise.
Applications of Sinc Function
Sinc Function is used in various applications like:
- Sinc function is popularly used in signal analysis system as it is has certain frequency analysis properties which makes it a useful function. This include tasks like filtering and interpolation of signals in communication.
- This function is widely used to understand Fourier transform theory. Transmission signals employ the use of rectangular signals as their input signals. In order to perform and analyse this signal it is necessary to convert it from time domain to frequency domain. sinc function appears in the frequency domain representation of a rectangular pulse and helps to understand it.
- These signals are largely used in pulse shaping and interpolation . Due to the unique shape of sinc Function it helps to interpolation of signals. It reconstructs regular signals from sampled data which are further used in processing.
- It is employed in the study of optics in phenomenon's like diffraction. The study of patterns from slit experiment throught rectangular apertures is done using sinc function.
- In general sinc function us widely used in communication systems during transmission and analysis because it helps in frequency domain representation of various time domain signals.
Conclusion
As we have seen Sinc Function play an important role in modern electronics. We have already discussed the unique graph of this signal along with other properties. As we discuss the uses of this signal we realize it is used in communication circuits, signal processing, Fourier Transforms, interpolation or for various other purposes. These applications signify the need to find appropriate methods to generate Sinc Function. There are different methods to generate this pulse and one method has been discussed with the readers. There are various other types of signals, each used for a different purpose.
Similar Reads
Signum Function
Signum Function is an important function in mathematics that helps us to know the sign of a real number. It is usually expressed as a function of a variable and denoted either by f(x) or by sgn(x). It may also be written as a sign(x). Signum Function also has applications in various fields such as p
5 min read
Graphing Function
Graphing Function is the process of illustrating the graph (the curve) for the function that corresponds to it. Plotting simple functions like linear, quadratic, cubic, et al. examples doesn’t pose a challenge; depicting functions of a more complex nature like rational, logarithmic, and others requi
13 min read
Square Function
A square function is also a quadratic function. A square function is represented as f(x) = x2. The graph of the square function is in the shape of a parabola or U- shaped. Based on the coefficient of x2 (highest degree in a square function), the graph may be U- shaped or Inverted U- shaped.In this a
8 min read
Tangent Function
Tangent Function: Trigonometric function tan(x) is called a tangent function it is one of the main six trigonometric functions and is generally written as tan x. The tangent function is the ratio of the opposite side and the adjacent side of the angle in consideration in a right-angled triangle. In
7 min read
Stair Step Function
Python has a special arithmetic function called the "Stair Step Function" that behaves like steps on a staircase. It assigns constant values ​​to the specific intervals of its domain, resulting in a step-like graph. People also call these functions "piecewise constant functions" or "step functions".
11 min read
Trigonometric Functions
Trigonometric Functions, often simply called trig functions, are mathematical functions that relate the angles of a right triangle to the ratios of the lengths of its sides.Trigonometric functions are the basic functions used in trigonometry and they are used for solving various types of problems in
6 min read
Six Trigonometric Functions
Trigonometry can be defined as the branch of mathematics that determines and studies the relationships between the sides of a triangle and the angles subtended by them. Trigonometry is used in the case of right-angled triangles. Trigonometric functions define the relationships between the 3 sides an
3 min read
Bash Scripting - Functions
A Bash script is a plain text file. This file contains different commands for step-by-step execution. These commands can be written directly into the command line but from a reusability perceptive it is useful to store all of the inter-related commands for a specific task in a single file. We can us
6 min read
Many One Functions
Many-to-One or Many One Function is one of the various types of functions that represent relationships between different entities. As we know, a function is a very specific type of relation in which each input has a unique output. In a many-one function, many inputs can have the same output. For exa
7 min read
Function Generator
In the field of electronics engineering, scientists and researchers often require signals that can be fed as an input to various devices which can later test their devices on these signals. Devices like modulators, filters, and analog-to-digital convertors require some input signals and other signal
14 min read