Lesson 8: Basic Differentation Rules (slides)
- 1. Sec on 2.3 Basic Differenta on Rules V63.0121.011: Calculus I Professor Ma hew Leingang New York University . NYUMathematics
- 2. Announcements Quiz 1 this week on 1.1–1.4 Quiz 2 March 3/4 on 1.5, 1.6, 2.1, 2.2, 2.3 Midterm Monday March 7 in class
- 3. Objectives Understand and use these differen a on rules: the deriva ve of a constant func on (zero); the Constant Mul ple Rule; the Sum Rule; the Difference Rule; the deriva ves of sine and cosine.
- 4. Recall: the derivative Defini on Let f be a func on and a a point in the domain of f. If the limit f(a + h) − f(a) f(x) − f(a) f′ (a) = lim = lim h→0 h x→a x−a exists, the func on is said to be differen able at a and f′ (a) is the deriva ve of f at a.
- 5. The deriva ve … …measures the slope of the line through (a, f(a)) tangent to the curve y = f(x); …represents the instantaneous rate of change of f at a …produces the best possible linear approxima on to f near a.
- 6. Notation Newtonian nota on Leibnizian nota on dy d df f′ (x) y′ (x) y′ f(x) dx dx dx
- 7. Link between the notations f(x + ∆x) − f(x) ∆y dy f′ (x) = lim = lim = ∆x→0 ∆x ∆x→0 ∆x dx dy Leibniz thought of as a quo ent of “infinitesimals” dx dy We think of as represen ng a limit of (finite) difference dx quo ents, not as an actual frac on itself. The nota on suggests things which are true even though they don’t follow from the nota on per se
- 8. Outline Deriva ves so far Deriva ves of power func ons by hand The Power Rule Deriva ves of polynomials The Power Rule for whole number powers The Power Rule for constants The Sum Rule The Constant Mul ple Rule Deriva ves of sine and cosine
- 9. Derivative of the squaring function Example Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x).
- 10. Derivative of the squaring function Example Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x). Solu on f(x + h) − f(x) f′ (x) = lim h→0 h
- 11. Derivative of the squaring function Example Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)2 − x2 f (x) = lim = lim h→0 h h→0 h
- 12. Derivative of the squaring function Example Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)2 − x2 f (x) = lim = lim h→0 h h→0 h + 2xh + h − 2 x2 x2 = lim h→0 h
- 13. Derivative of the squaring function Example Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)2 − x2 f (x) = lim = lim h→0 h h→0 h + 2xh + h − x2 2 x2 2x + h2 h ¡ = lim = lim h→0 h h→0 h
- 14. Derivative of the squaring function Example Suppose f(x) = x2 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)2 − x2 f (x) = lim = lim h→0 h h→0 h + 2xh + h − x2 2 x2 2x + h2 h ¡ = lim = lim h→0 h h→0 h = lim (2x + h) = 2x. h→0
- 15. The second derivative If f is a func on, so is f′ , and we can seek its deriva ve. f′′ = (f′ )′ It measures the rate of change of the rate of change!
- 16. The second derivative If f is a func on, so is f′ , and we can seek its deriva ve. f′′ = (f′ )′ It measures the rate of change of the rate of change! Leibnizian nota on: d2 y d2 d2 f f(x) dx2 dx2 dx2
- 17. The squaring function and its derivatives y . x
- 18. The squaring function and its derivatives y . f x
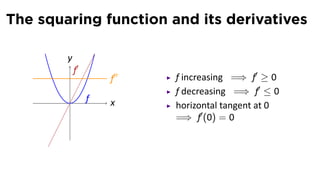
- 19. The squaring function and its derivatives y f′ f increasing =⇒ f′ ≥ 0 f decreasing =⇒ f′ ≤ 0 . f x horizontal tangent at 0 =⇒ f′ (0) = 0
- 20. The squaring function and its derivatives y f′ f′′ f increasing =⇒ f′ ≥ 0 f decreasing =⇒ f′ ≤ 0 . f x horizontal tangent at 0 =⇒ f′ (0) = 0
- 21. Derivative of the cubing function Example Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x).
- 22. Derivative of the cubing function Example Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)3 − x3 f (x) = lim = lim h→0 h h→0 h
- 23. Derivative of the cubing function Example Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)3 − x3 f (x) = lim = lim h→0 h h→0 h x3 + 3x2 h + 3xh2 + h3 − 3 x = lim h→0 h
- 24. Derivative of the cubing function Example Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)3 − x3 f (x) = lim = lim h→0 h h→0 h 1 2 ! ¡ ! ¡ x3 + 2 2 3x h + 3xh + h 3 − 3 x 3x2 + h ¡ 3xh2 + ¡ h3 = lim = lim h→0 h h→0 h
- 25. Derivative of the cubing function Example Suppose f(x) = x3 . Use the defini on of deriva ve to find f′ (x). Solu on ′ f(x + h) − f(x) (x + h)3 − x3 f (x) = lim = lim h→0 h h→0 h 1 2 ! ¡ ! ¡ x3 2 2 3x h + 3xh + h + 3 − 3 x 3x2 + h ¡ 3xh2 + ¡ h3 = lim = lim h→0 ( 2 h ) h→0 h = lim 3x + 3xh + h2 = 3x2 . h→0
- 26. The cubing function and its derivatives y . x
- 27. The cubing function and its derivatives y f . x
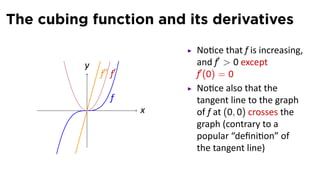
- 28. The cubing function and its derivatives No ce that f is increasing, y and f′ 0 except f′ f′ (0) = 0 f . x
- 29. The cubing function and its derivatives No ce that f is increasing, y and f′ 0 except f′′ f′ f′ (0) = 0 f . x
- 30. The cubing function and its derivatives No ce that f is increasing, y and f′ 0 except f′′ f′ f′ (0) = 0 No ce also that the f tangent line to the graph . x of f at (0, 0) crosses the graph (contrary to a popular “defini on” of the tangent line)
- 31. Derivative of the square root Example √ Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on.
- 32. Derivative of the square root Example √ Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on. Solu on √ √ ′ f(x + h) − f(x) x+h− x f (x) = lim = lim h→0 h h→0 h
- 33. Derivative of the square root Example √ Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on. Solu on √ √ ′ f(x + h) − f(x) x+h− x f (x) = lim = lim h→0 √ h h→0 h √ √ √ x+h− x x+h+ x = lim ·√ √ h→0 h x+h+ x
- 34. Derivative of the square root Example √ Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on. Solu on √ √ ′ f(x + h) − f(x) x+h− x f (x) = lim = lim h→0 √ h h→0 h √ √ √ x+h− x x+h+ x = lim ·√ √ h→0 h x+h+ x (x + h) − x ¡ ¡ = lim (√ √ ) h→0 h x+h+ x
- 35. Derivative of the square root Example √ Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on. Solu on √ √ ′ f(x + h) − f(x) x+h− x f (x) = lim = lim h→0 √ h h→0 h √ √ √ x+h− x x+h+ x = lim ·√ √ h→0 h x+h+ x (x + h) − x ¡ ¡ h = lim (√ √ ) = lim (√ √ ) h→0 h x+h+ x h x+h+ x h→0
- 36. Derivative of the square root Example √ Suppose f(x) = x = x1/2 . Fnd f′ (x) with the defini on. Solu on √ √ ′ f(x + h) − f(x) x+h− x f (x) = lim = lim h→0 √ h h→0 h √ √ √ x+h− x x+h+ x = lim ·√ √ h→0 h x+h+ x (x + h) − x ¡ ¡ h 1 = lim (√ √ ) = lim (√ √ )= √ h→0 h x+h+ x h x+h+ x h→0 2 x
- 37. The square root and its derivatives y . x
- 38. The square root and its derivatives y f . x
- 39. The square root and its derivatives y f Here lim+ f′ (x) = ∞ and f x→0 f′ is not differen able at 0 . x
- 40. The square root and its derivatives y f Here lim+ f′ (x) = ∞ and f x→0 f′ is not differen able at 0 . x No ce also lim f′ (x) = 0 x→∞
- 41. Derivative of the cube root Example √ Suppose f(x) = 3 x = x1/3 . Find f′ (x).
- 42. Derivative of the cube root Example √ Suppose f(x) = 3 x = x1/3 . Find f′ (x). Solu on f(x + h) − f(x) (x + h)1/3 − x1/3 f′ (x) = lim = lim h→0 h h→0 h
- 43. Derivative of the cube root Example √ Suppose f(x) = 3 x = x1/3 . Find f′ (x). Solu on f(x + h) − f(x) (x + h)1/3 − x1/3 f′ (x) = lim = lim h→0 h h→0 h (x + h) − x 1/3 1/3 (x + h) + (x + h)1/3 x1/3 + x2/3 2/3 = lim · h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3
- 44. Derivative of the cube root Example √ Suppose f(x) = 3 x = x1/3 . Find f′ (x). Solu on f(x + h) − f(x) (x + h)1/3 − x1/3 f′ (x) = lim = lim h→0 h h→0 h (x + h) − x 1/3 1/3 (x + h) + (x + h)1/3 x1/3 + x2/3 2/3 = lim · h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3 (x + h) − x ¡ ¡ = lim 2/3 + (x + h)1/3 x1/3 + x2/3 ) h→0 h ((x + h)
- 45. Derivative of the cube root Example √ Suppose f(x) = 3 x = x1/3 . Find f′ (x). Solu on f(x + h) − f(x) (x + h)1/3 − x1/3 f′ (x) = lim = lim h→0 h h→0 h (x + h) − x 1/3 1/3 (x + h) + (x + h)1/3 x1/3 + x2/3 2/3 = lim · h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3 (x + h) − x ¡ ¡ = lim 2/3 + (x + h)1/3 x1/3 + x2/3 ) h→0 h ((x + h) h = lim 2/3 + (x + h)1/3 x1/3 + x2/3 ) h→0 ((x + h) h
- 46. Derivative of the cube root Example √ Suppose f(x) = 3 x = x1/3 . Find f′ (x). Solu on f(x + h) − f(x) (x + h)1/3 − x1/3 f′ (x) = lim = lim h→0 h h→0 h (x + h) − x 1/3 1/3 (x + h) + (x + h)1/3 x1/3 + x2/3 2/3 = lim · h→0 h (x + h)2/3 + (x + h)1/3 x1/3 + x2/3 (x + h) − x ¡ ¡ = lim 2/3 + (x + h)1/3 x1/3 + x2/3 ) h→0 h ((x + h) h 1 = lim 2/3 + (x + h)1/3 x1/3 + x2/3 ) = 2/3 h→0 ((x + h) h 3x
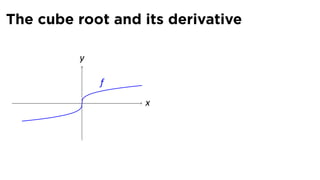
- 47. The cube root and its derivative y . x
- 48. The cube root and its derivative y f . x
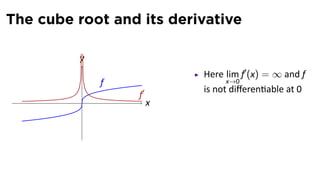
- 49. The cube root and its derivative y Here lim f′ (x) = ∞ and f f x→0 is not differen able at 0 f′ . x
- 50. The cube root and its derivative y Here lim f′ (x) = ∞ and f f x→0 is not differen able at 0 f′ . x No ce also lim f′ (x) = 0 x→±∞
- 51. One more Example Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x).
- 52. One more Example Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x). Solu on f(x + h) − f(x) (x + h)2/3 − x2/3 f′ (x) = lim = lim h→0 h h→0 h
- 53. One more Example Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x). Solu on f(x + h) − f(x) (x + h)2/3 − x2/3 f′ (x) = lim = lim h→0 h h→0 h 1/3 ( ) (x + h) − x 1/3 = lim · (x + h) + x 1/3 1/3 h→0 h
- 54. One more Example Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x). Solu on f(x + h) − f(x) (x + h)2/3 − x2/3 f′ (x) = lim = lim h→0 h h→0 h 1/3 ( ) (x + h) − x 1/3 = lim · (x + h) + x 1/3 1/3 h→0 ( h) 1 −2/3 = 3x 2x1/3
- 55. One more Example Suppose f(x) = x2/3 . Use the defini on of deriva ve to find f′ (x). Solu on f(x + h) − f(x) (x + h)2/3 − x2/3 f′ (x) = lim = lim h→0 h h→0 h 1/3 ( ) (x + h) − x 1/3 = lim · (x + h) + x 1/3 1/3 h→0 ( h) 1 −2/3 = 3x 2x1/3 = 2 x−1/3 3
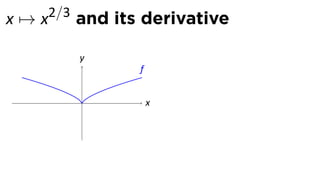
- 56. x → x2/3 and its derivative y . x
- 57. x → x2/3 and its derivative y f . x
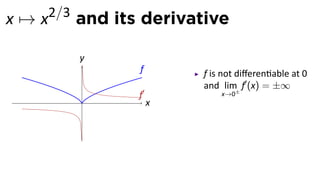
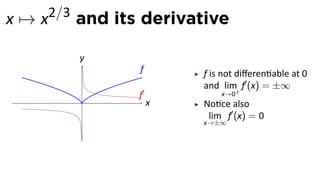
- 58. x → x2/3 and its derivative y f f is not differen able at 0 and lim± f′ (x) = ±∞ f′ x→0 . x
- 59. x → x2/3 and its derivative y f f is not differen able at 0 and lim± f′ (x) = ±∞ f′ x→0 . x No ce also lim f′ (x) = 0 x→±∞
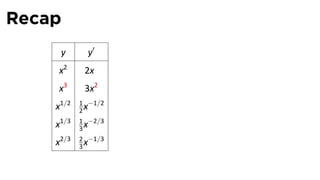
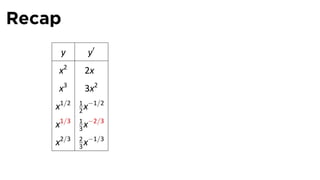
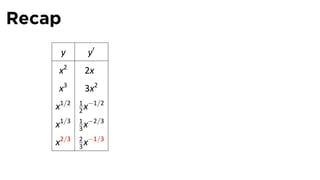
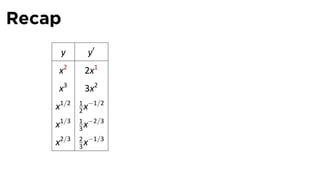
- 60. Recap y y′ x2 2x x3 3x2 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 61. Recap y y′ x2 2x x3 3x2 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 62. Recap y y′ x2 2x x3 3x2 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 63. Recap y y′ x2 2x x3 3x2 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 64. Recap y y′ x2 2x x3 3x2 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 65. Recap y y′ x2 2x1 x3 3x2 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
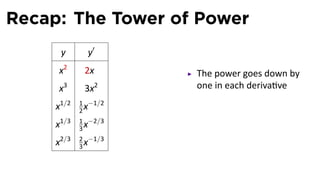
- 66. Recap: The Tower of Power y y′ x2 2x1 The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 67. Recap: The Tower of Power y y′ x2 2x The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 68. Recap: The Tower of Power y y′ x2 2x The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 69. Recap: The Tower of Power y y′ x2 2x The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 70. Recap: The Tower of Power y y′ x2 2x The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
- 71. Recap: The Tower of Power y y′ x2 2x The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 x1/2 2x 1 −2/3 x1/3 3x 2 −1/3 x2/3 3x
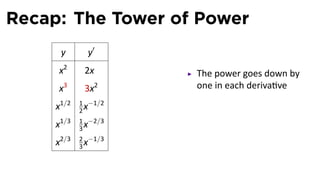
- 72. Recap: The Tower of Power y y′ x2 2x The power goes down by x 3 3x2 one in each deriva ve 1 −1/2 The coefficient in the x1/2 2x deriva ve is the power of 1 −2/3 x1/3 3x the original func on 2 −1/3 x2/3 3x
- 73. The Power Rule There is moun ng evidence for Theorem (The Power Rule) Let r be a real number and f(x) = xr . Then f′ (x) = rxr−1 as long as the expression on the right-hand side is defined. Perhaps the most famous rule in calculus We will assume it as of today We will prove it many ways for many different r.
- 74. The other Tower of Power
- 75. Outline Deriva ves so far Deriva ves of power func ons by hand The Power Rule Deriva ves of polynomials The Power Rule for whole number powers The Power Rule for constants The Sum Rule The Constant Mul ple Rule Deriva ves of sine and cosine
- 76. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it)
- 77. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) Proof. We have ∑ n (x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) = n ck xk hn−k n copies k=0
- 78. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) Proof. We have ∑ n (x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) = n ck xk hn−k n copies k=0
- 79. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) Proof. We have ∑ n (x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) = n ck xk hn−k n copies k=0
- 80. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) Proof. We have ∑ n (x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) = n ck xk hn−k n copies k=0
- 81. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) Proof. We have ∑ n (x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) = n ck xk hn−k n copies k=0
- 82. Remember your algebra Fact Let n be a posi ve whole number. Then (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) Proof. We have ∑ n (x + h) = (x + h) · (x + h) · (x + h) · · · (x + h) = n ck xk hn−k n copies k=0
- 83. Pascal’s Triangle . 1 1 1 1 2 1 1 3 3 1 (x + h)0 = 1 1 4 6 4 1 (x + h)1 = 1x + 1h (x + h)2 = 1x2 + 2xh + 1h2 1 5 10 10 5 1 (x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3 1 6 15 20 15 6 1 ... ...
- 84. Pascal’s Triangle . 1 1 1 1 2 1 1 3 3 1 (x + h)0 = 1 1 4 6 4 1 (x + h)1 = 1x + 1h (x + h)2 = 1x2 + 2xh + 1h2 1 5 10 10 5 1 (x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3 1 6 15 20 15 6 1 ... ...
- 85. Pascal’s Triangle . 1 1 1 1 2 1 1 3 3 1 (x + h)0 = 1 1 4 6 4 1 (x + h)1 = 1x + 1h (x + h)2 = 1x2 + 2xh + 1h2 1 5 10 10 5 1 (x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3 1 6 15 20 15 6 1 ... ...
- 86. Pascal’s Triangle . 1 1 1 1 2 1 1 3 3 1 (x + h)0 = 1 1 4 6 4 1 (x + h)1 = 1x + 1h (x + h)2 = 1x2 + 2xh + 1h2 1 5 10 10 5 1 (x + h)3 = 1x3 + 3x2 h + 3xh2 + 1h3 1 6 15 20 15 6 1 ... ...
- 87. Proving the Power Rule Theorem (The Power Rule) d n Let n be a posi ve whole number. Then x = nxn−1 . dx
- 88. Proving the Power Rule Theorem (The Power Rule) d n Let n be a posi ve whole number. Then x = nxn−1 . dx Proof. As we showed above, (x + h)n = xn + nxn−1 h + (stuff with at least two hs in it) (x + h)n − xn nxn−1 h + (stuff with at least two hs in it) So = h h = nxn−1 + (stuff with at least one h in it) and this tends to nxn−1 as h → 0.
- 89. The Power Rule for constants? Theorem d Let c be a constant. Then c=0 dx
- 90. The Power Rule for constants? d 0 Theorem like x = 0x−1 d dx Let c be a constant. Then c = 0. . dx
- 91. The Power Rule for constants? d 0 Theorem like x = 0x−1 d dx Let c be a constant. Then c = 0. . dx Proof. Let f(x) = c. Then f(x + h) − f(x) c − c = =0 h h So f′ (x) = lim 0 = 0. h→0
- 92. . Calculus
- 93. Recall the Limit Laws Fact Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then x→a x→a 1. lim [f(x) + g(x)] = L + M x→a 2. lim [f(x) − g(x)] = L − M x→a 3. lim [cf(x)] = cL x→a 4. . . .
- 94. Adding functions Theorem (The Sum Rule) Let f and g be func ons and define (f + g)(x) = f(x) + g(x) Then if f and g are differen able at x, then so is f + g and (f + g)′ (x) = f′ (x) + g′ (x). Succinctly, (f + g)′ = f′ + g′ .
- 95. Proof of the Sum Rule Proof. Follow your nose: (f + g)(x + h) − (f + g)(x) (f + g)′ (x) = lim h→0 h
- 96. Proof of the Sum Rule Proof. Follow your nose: (f + g)(x + h) − (f + g)(x) (f + g)′ (x) = lim h→0 h f(x + h) + g(x + h) − [f(x) + g(x)] = lim h→0 h
- 97. Proof of the Sum Rule Proof. Follow your nose: (f + g)(x + h) − (f + g)(x) (f + g)′ (x) = lim h→0 h f(x + h) + g(x + h) − [f(x) + g(x)] = lim h→0 h f(x + h) − f(x) g(x + h) − g(x) = lim + lim h→0 h h→0 h
- 98. Proof of the Sum Rule Proof. Follow your nose: (f + g)(x + h) − (f + g)(x) (f + g)′ (x) = lim h→0 h f(x + h) + g(x + h) − [f(x) + g(x)] = lim h→0 h f(x + h) − f(x) g(x + h) − g(x) = lim + lim h→0 h h→0 h ′ ′ = f (x) + g (x)
- 99. Scaling functions Theorem (The Constant Mul ple Rule) Let f be a func on and c a constant. Define (cf)(x) = cf(x) Then if f is differen able at x, so is cf and (cf)′ (x) = c · f′ (x) Succinctly, (cf)′ = cf′ .
- 100. Proof of Constant Multiple Rule Proof. Again, follow your nose. (cf)(x + h) − (cf)(x) (cf)′ (x) = lim h→0 h
- 101. Proof of Constant Multiple Rule Proof. Again, follow your nose. (cf)(x + h) − (cf)(x) cf(x + h) − cf(x) (cf)′ (x) = lim = lim h→0 h h→0 h
- 102. Proof of Constant Multiple Rule Proof. Again, follow your nose. (cf)(x + h) − (cf)(x) cf(x + h) − cf(x) (cf)′ (x) = lim = lim h→0 h h→0 h f(x + h) − f(x) = c lim h→0 h
- 103. Proof of Constant Multiple Rule Proof. Again, follow your nose. (cf)(x + h) − (cf)(x) cf(x + h) − cf(x) (cf)′ (x) = lim = lim h→0 h h→0 h f(x + h) − f(x) = c lim = c · f′ (x) h→0 h
- 104. Derivatives of polynomials Example d ( 3 ) Find 2x + x4 − 17x12 + 37 dx
- 105. Derivatives of polynomials Example d ( 3 ) Find 2x + x4 − 17x12 + 37 dx Solu on d ( 3 ) d ( 3) d d ( ) d 2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37) dx dx dx dx dx
- 106. Derivatives of polynomials Example d ( 3 ) Find 2x + x4 − 17x12 + 37 dx Solu on d ( 3 ) d ( 3) d d ( ) d 2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37) dx dx dx dx dx d d d = 2 x3 + x4 − 17 x12 + 0 dx dx dx
- 107. Derivatives of polynomials Example d ( 3 ) Find 2x + x4 − 17x12 + 37 dx Solu on d ( 3 ) d ( 3) d d ( ) d 2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37) dx dx dx dx dx d d d = 2 x3 + x4 − 17 x12 + 0 dx dx dx = 2 · 3x + 4x − 17 · 12x11 2 3
- 108. Derivatives of polynomials Example d ( 3 ) Find 2x + x4 − 17x12 + 37 dx Solu on d ( 3 ) d ( 3) d d ( ) d 2x + x4 − 17x12 + 37 = 2x + x4 + −17x12 + (37) dx dx dx dx dx d d d = 2 x3 + x4 − 17 x12 + 0 dx dx dx = 2 · 3x + 4x − 17 · 12x11 2 3 = 6x2 + 4x3 − 204x11
- 109. Outline Deriva ves so far Deriva ves of power func ons by hand The Power Rule Deriva ves of polynomials The Power Rule for whole number powers The Power Rule for constants The Sum Rule The Constant Mul ple Rule Deriva ves of sine and cosine
- 110. Derivatives of Sine and Cosine Fact d sin x = ??? dx Proof. From the defini on:
- 111. Derivatives of Sine and Cosine Fact d sin x = ??? dx Proof. From the defini on: d sin(x + h) − sin x sin x = lim dx h→0 h
- 112. Angle addition formulas See Appendix A sin(A + B) = . A cos B + cos A sin B sin cos(A + B) = cos A cos B − sin A sin B
- 113. Derivatives of Sine and Cosine Fact d sin x = ??? dx Proof. From the defini on: d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x sin x = lim = lim dx h→0 h h→0 h
- 114. Derivatives of Sine and Cosine Fact d sin x = ??? dx Proof. From the defini on: d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x sin x = lim = lim dx h→0 h h→0 h cos h − 1 sin h = sin x · lim + cos x · lim h→0 h h→0 h
- 115. Two important trigonometric limits See Section 1.4 sin θ lim . =1 θ→0 θ cos θ − 1 sin θ θ lim =0 θ θ→0 θ . 1 − cos θ 1
- 116. Derivatives of Sine and Cosine Fact d sin x = ??? dx Proof. From the defini on: d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x sin x = lim = lim dx h→0 h h→0 h cos h − 1 sin h = sin x · lim + cos x · lim h→0 h h→0 h = sin x · 0 + cos x · 1
- 117. Derivatives of Sine and Cosine Fact d sin x = ??? dx Proof. From the defini on: d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x sin x = lim = lim dx h→0 h h→0 h cos h − 1 sin h = sin x · lim + cos x · lim h→0 h h→0 h = sin x · 0 + cos x · 1
- 118. Derivatives of Sine and Cosine Fact d sin x = cos x dx Proof. From the defini on: d sin(x + h) − sin x ( sin x cos h + cos x sin h) − sin x sin x = lim = lim dx h→0 h h→0 h cos h − 1 sin h = sin x · lim + cos x · lim h→0 h h→0 h = sin x · 0 + cos x · 1 = cos x
- 119. Illustration of Sine and Cosine y . x π −π 0 π π 2 2 sin x
- 120. Illustration of Sine and Cosine y . x π −π 0 π π cos x 2 2 sin x f(x) = sin x has horizontal tangents where f′ = cos(x) is zero.
- 121. Illustration of Sine and Cosine y . x π −π 0 π π cos x 2 2 sin x f(x) = sin x has horizontal tangents where f′ = cos(x) is zero. what happens at the horizontal tangents of cos?
- 122. Derivative of Cosine Fact d cos x = − sin x dx
- 123. Derivative of Cosine Fact d cos x = − sin x dx Proof. We already did the first. The second is similar (muta s mutandis): d cos(x + h) − cos x cos x = lim dx h→0 h
- 124. Derivative of Cosine Fact d cos x = − sin x dx Proof. We already did the first. The second is similar (muta s mutandis): d cos(x + h) − cos x (cos x cos h − sin x sin h) − cos x cos x = lim = lim dx h→0 h h→0 h
- 125. Derivative of Cosine Fact d cos x = − sin x dx Proof. We already did the first. The second is similar (muta s mutandis): d cos(x + h) − cos x (cos x cos h − sin x sin h) − cos x cos x = lim = lim dx h→0 h h→0 h cos h − 1 sin h = cos x · lim − sin x · lim h→0 h h→0 h
- 126. Derivative of Cosine Fact d cos x = − sin x dx Proof. We already did the first. The second is similar (muta s mutandis): d cos(x + h) − cos x (cos x cos h − sin x sin h) − cos x cos x = lim = lim dx h→0 h h→0 h cos h − 1 sin h = cos x · lim − sin x · lim h→0 h h→0 h = cos x · 0 − sin x · 1 = − sin x
- 127. Summary What have we learned today? The Power Rule
- 128. Summary What have we learned today? The Power Rule The deriva ve of a sum is the sum of the deriva ves The deriva ve of a constant mul ple of a func on is that constant mul ple of the deriva ve
- 129. Summary What have we learned today? The Power Rule The deriva ve of a sum is the sum of the deriva ves The deriva ve of a constant mul ple of a func on is that constant mul ple of the deriva ve The deriva ve of sine is cosine The deriva ve of cosine is the opposite of sine.














































































![Recall the Limit Laws
Fact
Suppose lim f(x) = L and lim g(x) = M and c is a constant. Then
x→a x→a
1. lim [f(x) + g(x)] = L + M
x→a
2. lim [f(x) − g(x)] = L − M
x→a
3. lim [cf(x)] = cL
x→a
4. . . .](https://image.slidesharecdn.com/lesson08-basicdifferentiationrules011slides-110219060329-phpapp02/85/Lesson-8-Basic-Differentation-Rules-slides-93-320.jpg)


![Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h
f(x + h) + g(x + h) − [f(x) + g(x)]
= lim
h→0 h](https://image.slidesharecdn.com/lesson08-basicdifferentiationrules011slides-110219060329-phpapp02/85/Lesson-8-Basic-Differentation-Rules-slides-96-320.jpg)
![Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h
f(x + h) + g(x + h) − [f(x) + g(x)]
= lim
h→0 h
f(x + h) − f(x) g(x + h) − g(x)
= lim + lim
h→0 h h→0 h](https://image.slidesharecdn.com/lesson08-basicdifferentiationrules011slides-110219060329-phpapp02/85/Lesson-8-Basic-Differentation-Rules-slides-97-320.jpg)
![Proof of the Sum Rule
Proof.
Follow your nose:
(f + g)(x + h) − (f + g)(x)
(f + g)′ (x) = lim
h→0 h
f(x + h) + g(x + h) − [f(x) + g(x)]
= lim
h→0 h
f(x + h) − f(x) g(x + h) − g(x)
= lim + lim
h→0 h h→0 h
′ ′
= f (x) + g (x)](https://image.slidesharecdn.com/lesson08-basicdifferentiationrules011slides-110219060329-phpapp02/85/Lesson-8-Basic-Differentation-Rules-slides-98-320.jpg)






























