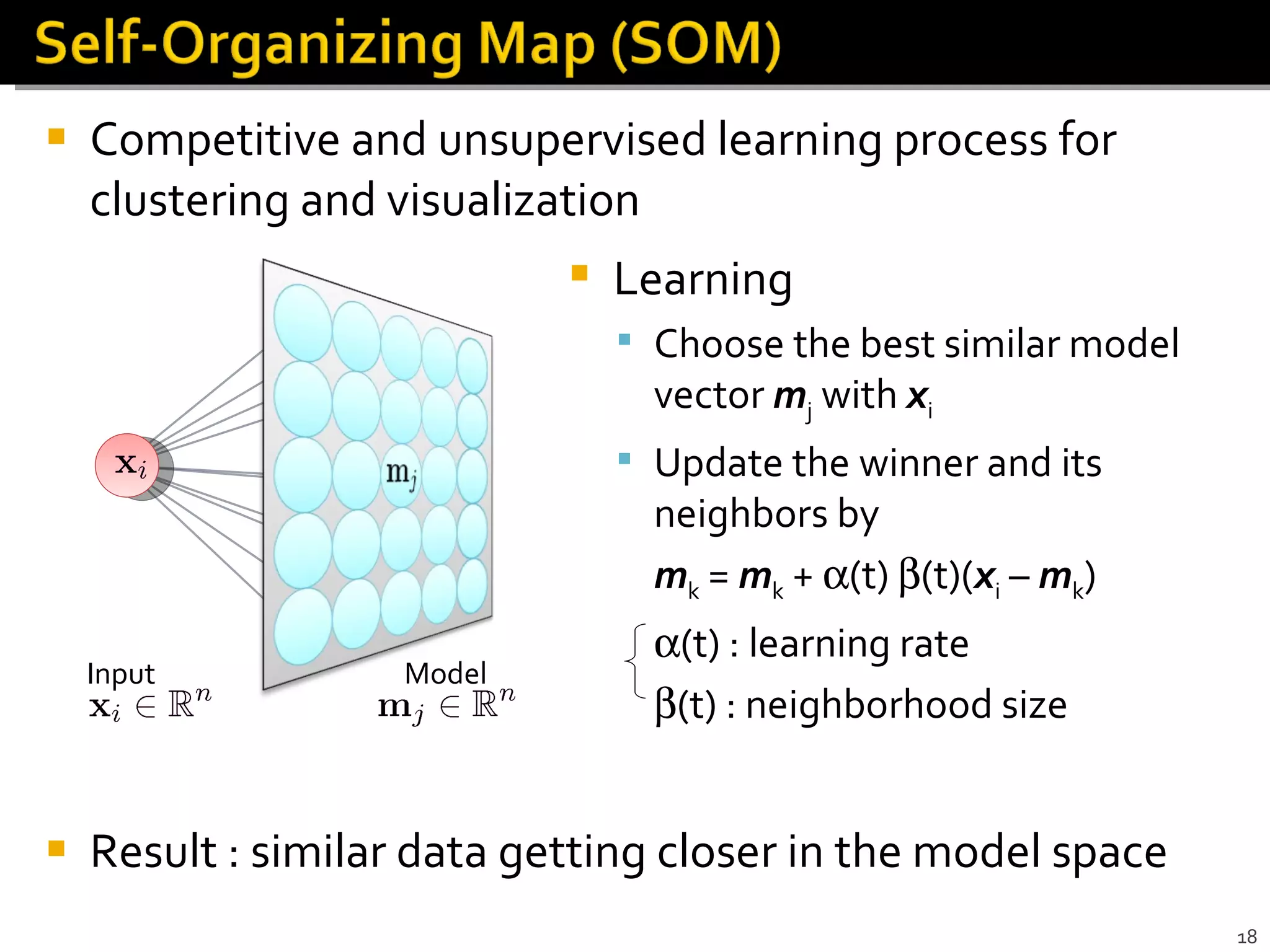
The document discusses machine learning concepts including supervised and unsupervised learning algorithms like clustering, dimensionality reduction, and classification. It also covers parallel computing strategies for machine learning like partitioning problems across distributed memory systems.